Задать граф матрицей смежности python

работа с графами в Python

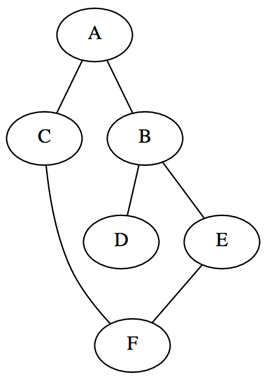
Будет использоваться ненаправленный связный граф V=6 E=6. Существует две популярные методики представления графов: матрица смежности (эффективна с плотными графами) и список связей (эффективно с разряженными графами). Будем использовать второй способ.

graph = 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E']>

2 Depth-First Search — Поиск вглубину

Алгоритм поиска вглубину: исследуем сначала все возможные вершины (из выбранного корня) доступные из текущей, прежде чем возвращаться назад. Данный алгоритм можно реализовать как рекурсивно, так и итеративно. Последовательность действий:

• Помечаем текущую вершину как посещённую
• Исследуем каждую соседнюю вершину не включённую в список уже посещённых
• Вариант с DFS and BFS in Python (модифицированный, т.к. set не поддерживает упорядоченность элементов)

graph = 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E']> def dfs(graph, start): visited, stack = [], [start] while stack: vertex = stack.pop() if vertex not in visited: visited.append(vertex) stack.extend(set(graph[vertex]) - set(visited)) return visited print(dfs(graph, 'A'))

• Вариант с DFS and BFS graph traversal (Python recipe) (модифицированный, т.к. для реализации стека нам необходимо добавлять элементы в конец списка, а не в начало)

graph = 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E']> def iteractive_dfs(graph, start, path=None): """iterative depth first search from start""" if path is None: path = [] q = [start] while q: v = q.pop() if v not in path: path = path + [v] q += graph[v] return path print(iteractive_dfs(graph, 'A'))

3 DFS Paths — поиск пути между двумя вершинами

graph = 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E']> def dfs_paths(graph, start, goal): stack = [(start, [start])] # (vertex, path) while stack: (vertex, path) = stack.pop() for next in set(graph[vertex]) - set(path): if next == goal: yield path + [next] else: stack.append((next, path + [next])) print(list(dfs_paths(graph, 'A', 'F')))

4 Bread-Firsth Search — Поиск вширину

Позволяет найти кратчайший путь между двумя вершинами. Довольно сложно реализовать рекурсивно, гораздо проще реализовать его с использованием очереди.

graph = 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E']> from queue import deque def bfs(graph, start): visited, queue = [], deque([start]) while queue: vertex = queue.pop() if vertex not in visited: visited.append(vertex) queue.extendleft(set(graph[vertex]) - set(visited)) return visited print(bfs(graph, 'A'))

5 BFS Paths

from queue import deque graph = 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E']> def bfs_paths(graph, start, goal): queue = deque([(start, [start])]) while queue: (vertex, path) = queue.pop() for next in set(graph[vertex]) - set(path): if next == goal: yield path + [next] else: queue.appendleft((next, path+[next])) print(list(bfs_paths(graph, 'A', 'F'))) def shortest_path(graph, start, goal): try: return next(bfs_paths(graph, start, goal)) except StopIteration: return None print(shortest_path(graph, 'A', 'F')) print(shortest_path(graph, 'E', 'D')) print(shortest_path(graph, 'A', 'D')) print(shortest_path(graph, 'F', 'D'))

[['A', 'C', 'F'], ['A', 'B', 'E', 'F']] ['A', 'C', 'F'] ['E', 'B', 'D'] ['A', 'B', 'D'] ['F', 'E', 'B', 'D']

Created: 2017-11-09 Thu 19:40

Источник

Введение в теорию графов в Python

Теория графов — обширная область исследования, основанная на простой идее об отдельных точках, известных как вершины, соединенных линиями, известными как ребра, каждая из которых может иметь связанные числовые значения, называемые весом, а также, возможно, направлением.

Эти простые наборы вершин, ребер, весов и направлений известны как графы (не путать с более знакомым графом данных или математической функцией) и могут использоваться для представления многих реальных ситуаций или абстрактных концепций. Если у вас есть граф, хранящийся в какой-то структуре данных, существует множество алгоритмов, которые можно применять для решения проблем, особенно задач оптимизации.

Этот пост является первым из многих, и в нем я разработаю структуру данных для хранения графика. В будущих публикациях я буду реализовывать некоторые алгоритмы, работающие с графами.

Практическое использование

Наиболее очевидное использование графиков — это представление географических местоположений и маршрутов между ними. На приведенном ниже графике представлены четыре шотландских города, а линии и числа представляют соединения и расстояния (в милях) между ними.

Вероятно, самая известная проблема в теории графов — это проблема коммивояжера. В этой задаче гипотетическому продавцу необходимо как можно более эффективно посетить несколько городов. Есть шесть возможных комбинаций — какую выбрать, чтобы минимизировать расстояние или время?

Это проблема для будущей публикации, но сейчас нам нужно создать структуру данных для хранения графа, и я начну с написания класса для этого.

Структуры данных графиков

Большая часть данных может быть легко помещена в какую-либо структуру строки / столбца, в Python это может быть список списков, словарь кортежей, какая-либо другая их комбинация или, возможно, ваши собственные пользовательские структуры данных. Графики немного запутаннее, но есть два основных способа их представить.

Первый называется списком смежности, и я буду использовать его здесь. Он состоит из списка вершин (например, городов), каждая из которых содержит список ребер (например, список других городов, с которыми он связан, с указанием расстояния).

График шотландских городов, который я буду использовать в этом проекте, будет выглядеть так, когда он представлен в списке смежности.

Здесь стоит отметить несколько моментов. Во-первых, каждое ребро существует дважды, например, есть ребро от Инвернесса до Абердина с весом (расстоянием) 103, а также одно ребро от Абердина до Инвернесса с таким же весом. Край не направлен, но, опуская одно из этих ребер, мы можем представить направленный край, например улицу с односторонним движением.

Во-вторых, в этом примере все города связаны со всеми остальными. Если бы мы добавили все города, поселки и деревни в Шотландии, ни один из них не был бы связан со всеми остальными; фактически у большинства из них были бы прямые дороги только к горстке других. Использование списка смежности эффективно, поскольку в нем должны храниться только фактические ребра.

Это подводит нас ко второму основному типу структур данных, используемых для представления графиков, матрице смежности. Это двухмерная сетка, которая выглядит так:

В этом случае память тратится мало, но если бы такая структура данных использовалась для представления всех городов, поселков и деревень в Шотландии, большая часть памяти была бы потрачена впустую. Поэтому списки смежности подходят только в том случае, если большинство или все вершины соединены.

Проект

Этот проект состоит из следующих четырех файлов, находящихся в репозитории Github.

Во-первых, есть пара очень простых классов для представления вершин и ребер. Это Vertex класс.

Помимо label , Vertex имеет список ребер, а также атрибут под названием visited , который будет использоваться в будущем для различных алгоритмов.

Класс Edge имеет атрибуты для (т. Е. Вершины, к которой он относится) и веса. Начальная вершина — это вершина, к которой прикреплено ребро.

Теперь давайте посмотрим на класс GraphAdjacencyList , основу этого проекта.

__в этом__

Ну, это красиво и просто, не так ли? Просто создайте пустой список.

__str__

Довольно утомительный, но важный метод, который обеспечивает аккуратное строковое представление объекта, в первую очередь для нас с помощью функции печати.

В приведенной выше таблице, демонстрирующей матрицу смежности, я показал края каждой вершины по горизонтали, но здесь они показаны вертикально, как мы сейчас увидим. Если у вершины нет ребер или если ребро не имеет веса, то отображаются пробелы.

add_vertex

Сначала мы проверяем, что вершина с данной меткой еще не существует, и, если нет, создается и добавляется новый объект Vertex.

add_edge

Нам нужно проверить, что ребро еще не существует, а также, что заданные метки вершин действительно существуют, что при необходимости вызывает ошибки. Если все в порядке, мы создаем новый объект Edge и добавляем его в вершину.

Если край не направлен, нам также необходимо добавить «обратный» край, что делается с помощью рекурсивного вызова add_edge. Этот вызов должен быть направлен на True, иначе метод попытается воссоздать первое ребро, что приведет к ошибке.

edit_vertex

Этот метод используется для переименования вершин, поэтому необходимо изменить атрибуты ребер на. Это делается путем перебора вершин и использования внутреннего цикла для перебора ребер. Обратите внимание, что возникает ошибка, если вершина с данной меткой не существует.

edit_edge

Этот метод изменяет веса ребер, перебирая вершины, чтобы найти вершину «от», а затем перебирая ее ребра, чтобы найти вершину «до». Если ребро не существует, возникает ошибка.

Обратный метод не работает: если есть еще ребро от вершины «до» к вершине «от», вес не меняется. Это сделано намеренно и допускает ситуации, когда веса различны в каждом направлении.

delete_vertex

Этот метод удаляет вершину с указанной меткой, а также все ребра в других вершинах, указывающие на нее. Обычно возникает ошибка, если вершина не существует.

delete_edge

Этот метод перебирает вершины, чтобы найти «от», а затем перебирает его ребра, чтобы найти «до», прежде чем удалять его. Как и в случае с edit_edge, метод не влияет на края в противоположном направлении.

__find_vertex_index

Это служебная функция, которая находит индекс вершины с заданной меткой, если таковой имеется.

__edge_exists

Эта функция проверяет, существует ли ребро между двумя заданными вершинами.

Наш GraphAdjacencyList класс завершен, поэтому нам просто нужно опробовать его в graphtheory.py.

В main мы сначала вызываем функцию для создания и заполнения графика данными о городах Шотландии, а затем распечатываем его.

Запустить программу

Запустите код с помощью этой команды…

… Что даст вам этот результат.

Функция edit_graph переводит названия городов на шотландский язык (Эдинбург на английском и на шотландском языках совпадает). Закомментируйте первый print в main , затем раскомментируйте вызов edit_graph и второй print . Запустите программу еще раз, и вы получите .

Я лишь поверхностно коснулся этой обширной темы, но теперь вы понимаете, что такое граф и какие структуры данных можно использовать для представления графа.

В следующих статьях я рассмотрю некоторые алгоритмы, которые можно применить к графу.

Источник