What is algorithm in javascript

What is algorithm in javascript

Чтобы найти шестое число в ряду, нам нужно найти сначала пятое и четвертое, то есть разделить задачу на более мелкие. При этом можно кешировать и повторно использовать результаты вычисления более мелких чисел – первого, второго и т.д.

Жадные алгоритмы (greedy algorithms)

Более сложный подход к решению проблем предполагает на каждом локальном этапе принятие решений, которые на данный момент являются оптимальными. Допускается, что конечное решение тоже будет оптимальным.

Требуется выдать конкретную сумму минимально возможным количеством монет разного достоинства (10 рублей, 5 рублей, 2 рубля, 1 рубль). Сначала набираем максимально возможную сумму монетами самого высокого достоинства (10 рублей). Потом переходим к пяти-рублевым и пытаемся набрать ими остаток и так далее.

Вычислительная сложность алгоритмов

Разные алгоритмы имеют разную эффективность. Например, очевидно, что если искомый элемент находится в самом конце массива, то метод полного перебора потребует больше времени, чем стратегия «разделяй и властвуй».

Для каждого алгоритма можно измерить вычислительную сложность (обозначается буквой O-большое). Это зависимость времени выполнения от количества элементов массива. Грубо говоря, чем она больше, тем менее эффективен алгоритм.

Также при оценке сложности следует учитывать дополнительное использование памяти, например, создание временных переменных.

В измерении вычислительной сложности алгоритмов полезно разобраться, чтобы использовать более эффективные.

Подробнее о нотации O-большое:

Какие алгоритмы нужно знать, чтобы стать хорошим программистом?

Это некорректный вопрос, так как хороший программист должен уметь самостоятельно выводить алгоритмы, а не просто выбирать из коллекции готовых решений. Гораздо важнее разобраться с подходами к решению задач.

В крайнем случае вы всегда можете найти нужный алгоритм в гугле, но для этого нужно хотя бы знать, что искать.

Для развития алгоритмической смекалки мы начнем с базовых структур и алгоритмов, а затем перейдем к более сложным.

Массивы

Массивы – очень популярная структура данных, которая к тому же уже реализована в JavaScript из коробки и имеет множество полезных методов для работы. В то же время это очень простая структура, что поможет нам разобраться со многими основными алгоритмами.

Описание структуры и основные операции

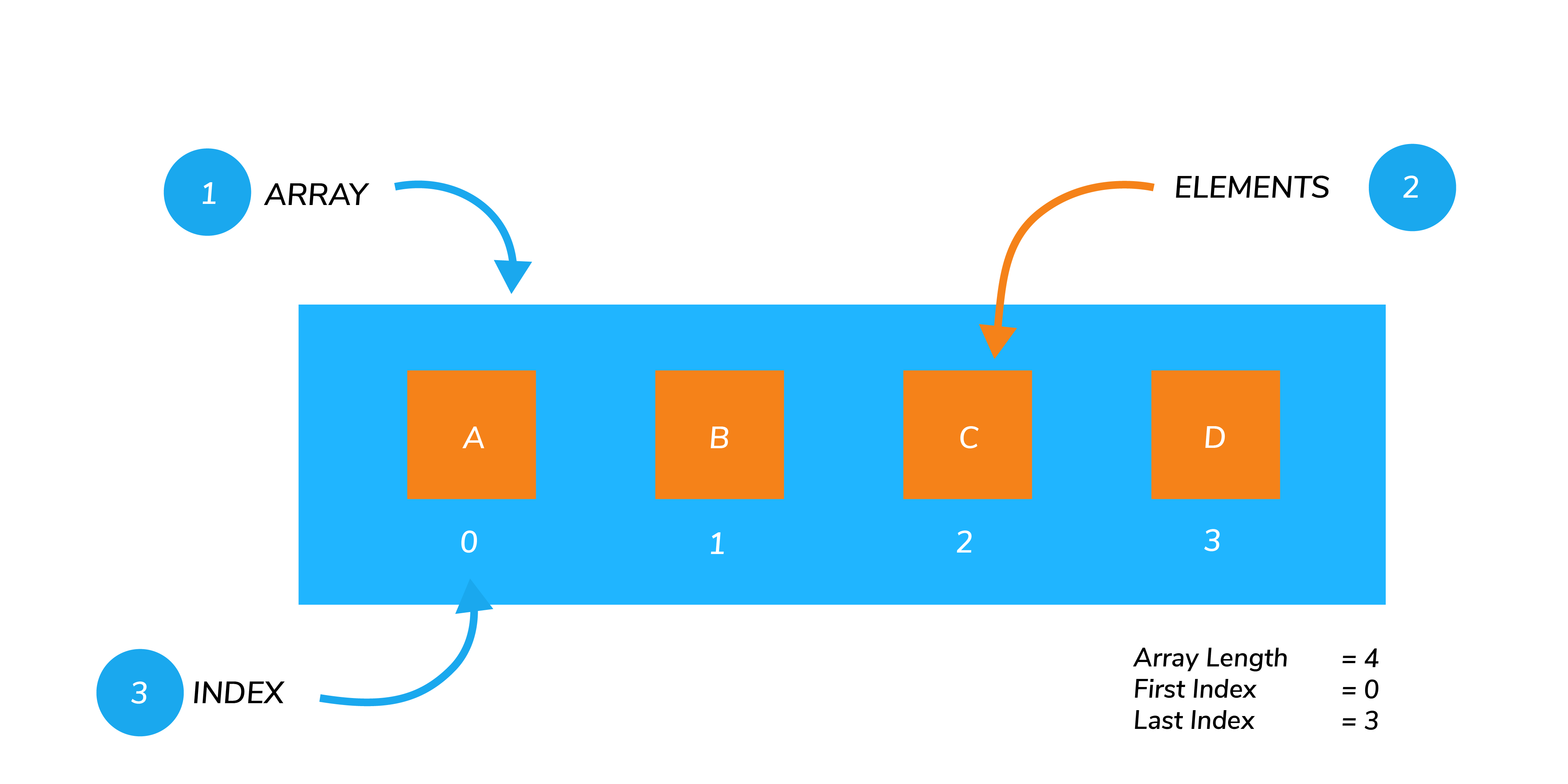
Массив в JavaScript – это самая простая упорядоченная коллекция элементов. Каждый элемент массива имеет свой порядковый номер (индекс), нумерация начинается с нуля. Таким образом, у массива есть начало (индекс 0) и конец.

Так как массивы упорядочены, к каждому элементу массива можно обратиться по его индексу – это прямое обращение. Если вы хотите узнать, какой элемент стоит в массиве на третьем месте, вам не придется перебирать сначала первый и второй.

Массивы в JavaScript предоставляют множество полезных алгоритмов для работы с данными, например, для вставки и удаления элемента.

Это очень простые алгоритмы: они изменяют только длину массива, а нумерация предыдущих элементов остается прежней.

• Array.prototype.unshift – в ставка элемента (элементов) в начало массива.
• Array.prototype.shift – у даление элемента из начала массива.

Казалось бы, почти то же самое, однако эти алгоритмы уже существенно сложнее. Если вы производите добавляете или удаляете элементы в начале массива, необходимо изменить нумерацию всех последующих элементов.

Производительность

Если в массиве 5 элементов, и вы добавляете в начало ещё один, то кроме непосредственно вставки нового элемента, нужно перебрать пять старых и изменить индекс каждого из них. Это пять дополнительных действий.

Осталось лишь повторить всю последовательность действий, пока не всплывут все элементы.

Реализация на JavaScript:

• Первый цикл отслеживает индекс последнего всплывшего элемента. На каждой итерации он будет уменьшаться.
• Второй цикл – это индекс активного элемента на текущей итерации. Он будет начинаться с нуля и продолжаться до элементов, «всплывших» на предыдущих итерациях. Так как они уже отсортированы, не имеет смысла снова их сравнивать.

Это лишь один из способов реализации пузырьковой сортировки, подробнее об этом алгоритме вы можете прочитать в нашей статье: Пузырьковая сортировка на JavaScript

Пузырьковая сортировка является устойчивой, а ее временная сложность составляет O(N²) в худшем случае. Это означает, что для массива с n элементами нужно совершить n 2 операций: для каждого из элементов приходится сделать проход по всем остальным элементам массива. Реальное значение чуть меньше чем n 2 , но при расчете сложности алгоритма все коэффициенты отбрасываются. В лучшем случае, если массив уже отсортирован, потребуется всего n операций.

Сортировка выбором

Этот алгоритм похож на сортировку пузырьком: он на каждой итерации отсортировывает один элемент, только собираются они не в конце массива, а в начале.

Алгоритм также начинает с первого элемента массива и движется направо. Он сравнивает элементы попарно и отбирает минимальный из них. Найденный минимум меняется местами с первым не отсортированным элементом в начале массива.

Реализация на JavaScript:

Начинаем с нулевого элемента. На каждой итерации ищем минимум в неотсортированной части и добавляем его к отсортированной.

В отличие от пузырьковой, сортировка выбором неустойчива, но сложность у нее такая же – O(N²).

Сортировка вставками

Полагается, что начало массива уже отсортировано (изначально 1 элемент). Алгоритм берет первый неотсортированный элемент (индекс 1) и последовательно сравнивает его с отсортированными, находя нужное место. После этого длина отсортированной части увеличивается (теперь уже два отсортированных элемента) и алгоритм переходит к следующему элементу (индекс 2).

Реализация на JavaScript:

Начинаем с первого элемента (нулевой считаем отсортированным). На каждой итерации сравниваем активный элемент с отсортированными и находим его место.

Сложность сортировки вставками такая же, как у предыдущих алгоритмов – O(N²) в худшем случае (если массив отсортирован в обратном порядке). Алгоритм является стабильным.

Сортировка слиянием

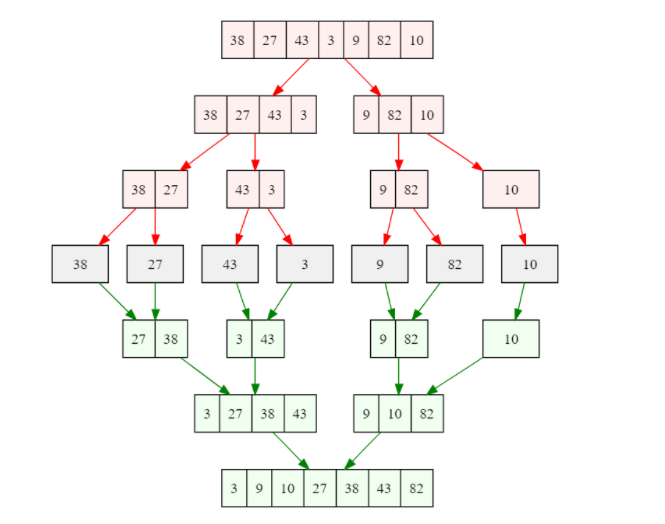
Сортировка слиянием – отличный пример применения стратегии «разделяй и властвуй».

Алгоритм состоит из трех этапов:

• Исходный массив разделяется на две примерно равные части.
• Каждая часть сортируется отдельно.
• Обе отсортированные части объединяются в один массив.

Этап 2 выглядит весьма таинственно, ведь он ничего не говорит о том, как именно происходит сортировка частей исходного массива. На самом деле к ним применяется тот же алгоритм (рекурсивное решение задачи). Каждая часть в свою очередь делится на две части, каждая из которых сортируется отдельно, а затем эти части вновь объединяются. Рекурсивное разделение осуществляется до тех пор, пока в каждой части не будет находиться всего один элемент – массив из одного элемента однозначно является отсортированным.

На третьем этапе тоже загадка – как именно происходит объединение двух частей в один массив. Тут все довольно просто: на каждом шаге мы берем первые элементы массивов, сравниваем их, выбираем меньший и добавляем в новый объединенный массив.

Реализация на JavaScript:

Основная функция сортировки mergeSort делит массив на две части с помощью метода Array.prototype.slice , отправляет каждую часть на рекурсивную сортировку, а затем снова объединяет их с помощью функции mergeSortedArrays .

Вспомогательная функция mergeSortedArrays начинает с нулевых элементов обоих массивов, сравнивает их и находит минимальный. Для того массива, в котором нашелся минимум, активный индекс сдвигается вправо. Сравнения происходят пока один из массивов не закончится, тогда остаток другого просто присоединяется к результирующему массиву.

Сортировка слиянием является стабильной. Для нее требуется выполнить n * log(n) операций. Это эффективнее, чем предыдущие алгоритмы.

Быстрая сортировка

Алгоритм быстрой сортировки (сортировка Хоара), как ни странно, является одним из самых быстрых алгоритмов сортировки. Он немного похож и на пузырьковую сортировку, и на сортировку слиянием, так как тоже использует стратегию «разделяй и властвуй».

• Сначала в массиве выбирается опорный элемент (пивот). Выбрать его можно любым способом: например, взять первый, средний или случайный элемент. От способа выбора во многом зависит эффективность алгоритма.
• Затем все остальные элементы сравниваются с опорным и переставляются так, чтобы все элементы, которые меньше опорного оказались до него, а все, которые больше – после. Под больше и меньше здесь имеется в виду результат сортировки. На этом этапе в массиве сначала идут все элементы меньше опорного (для которых компаратор вернул отрицательное число), затем опорный, а затем все элементы больше опорного (компаратор вернул положительное число).
• И наконец для групп «меньше» и «больше» рекурсивно выполняется тот же самый алгоритм. Сам опорный элемент может быть включен в одну из групп.

Реализация на JavaScript:

Реализация на JavaScript могла бы выглядеть вот так:

function linearSearch(arr, wanted) < let found = []; arr.forEach((el, i) =>< if (comparator(el, wanted) === 0) found.push(i); >; return found; > 

Функция linearSearch находит все подходящие элементы в отличие от Array.prototype.find , которая ограничивается только первым. Очевидно, что сложность этого алгоритма равна O(n), так как в худшем случае придется перебрать каждый элемент массива.

Бинарный поиск (разделяй и властвуй)

Второй алгоритм поиска использует принцип разделяй и властвуй и является более эффективным. Вот только ему для работы непременно нужен отсортированный массив, иначе ничего не получится.

Бинарный поиск ищет нужный элемент по принципу словаря – открывает на середине и выбирает нужную половину, а вторую отбрасывает.

Реализация на JavaScript:

function binarySearch(arr, wanted) < // Границы подмассива для поиска let start = 0; let end = arr.length - 1; while (start return -1; // ничего не нашлось > 

Сложность этого алгоритма составляет O(log(n)), но не забывайте, что ему требуется предварительная сортировка.

Заключение

Итак, мы разобрались с основными понятиями, поближе познакомились со встроенными в JavaScript массивами и даже реализовали 7 популярных алгоритмов для работы с ними. В следующей статье цикла перейдем к более сложным структурам и алгоритмам.

Источник