Взаимно корреляционная функция python

Как рассчитать взаимную корреляцию в Python

Взаимная корреляция — это способ измерения степени сходства между временным рядом и запаздывающей версией другого временного ряда.

Этот тип корреляции полезен для расчета, потому что он может сказать нам, предсказывают ли значения одного временного ряда будущие значения другой временной ряд. Другими словами, он может сказать нам, является ли один временной ряд опережающим индикатором для другого временного ряда.

Этот тип корреляции используется во многих областях, в том числе:

Бизнес: Расходы на маркетинг часто считаются опережающим индикатором будущих доходов бизнеса. Например, если бизнес тратит ненормально денег на маркетинг в течение одного квартала, то ожидается, что общий доход будет высоким x кварталов спустя.

Экономика: Индекс потребительского доверия (CCI) считается опережающим индикатором валового внутреннего продукта (ВВП) страны. Например, если CCI высокий в течение определенного месяца, ВВП, вероятно, будет выше x месяцев спустя.

В следующем примере показано, как вычислить взаимную корреляцию между двумя временными рядами в Python.

Пример: как рассчитать взаимную корреляцию в Python

Предположим, у нас есть следующее время серия на Python, показывающая общие расходы на маркетинг (в тысячах) для определенной компании, а также общий доход (в тысячах) за 12 месяцев подряд:

import numpy as np #define data marketing = np.array([3, 4, 5, 5, 7, 9, 13, 15, 12, 10, 8, 8]) revenue = np.array([21, 19, 22, 24, 25, 29, 30, 34, 37, 40, 35, 30]) 

Мы можем рассчитать взаимную корреляцию для каждого лага между двумя временными рядами, используя функцию ccf() из пакета statsmodels следующим образом:

import statsmodels.api as sm #calculate cross correlation sm.tsa.stattools.ccf(marketing, revenue, adjusted=False) array([ 0.77109358, 0.46238654, 0.19352232, -0.06066296, -0.28159595, -0.44531104, -0.49159463, -0.35783655, -0.15697476, -0.03430078, 0.01587722, 0.0070399 ])

Вот как интерпретировать этот вывод:

• Взаимная корреляция при lag 0 составляет 0,771
• Взаимная корреляция при lag 1 составляет 0,462
• Взаимная корреляция при lag 2 составляет 0,194
• Взаимная корреляция при lag 3 составляет -0,061

Обратите внимание, что корреляция между двумя временными рядами становится все менее и менее положительной по мере увеличения количества задержек. Это говорит нам о том, что расходы на маркетинг в течение определенного месяца позволяют прогнозировать доход через один или два месяца, но не позволяют прогнозировать доход более чем через два месяца.

Это интуитивно понятно мы ожидаем, что высокие расходы на маркетинг в данном месяце предсказывают увеличение дохода в течение следующих двух месяцев, но не обязательно предсказывают доход через несколько месяцев в будущем.

Источник

numpy.correlate#

This function computes the correlation as generally defined in signal processing texts:

with a and v sequences being zero-padded where necessary and \(\overline x\) denoting complex conjugation.

Parameters : a, v array_like

Refer to the convolve docstring. Note that the default is ‘valid’, unlike convolve , which uses ‘full’.

old_behavior bool

old_behavior was removed in NumPy 1.10. If you need the old behavior, use multiarray.correlate.

Returns : out ndarray

Discrete cross-correlation of a and v.

Discrete, linear convolution of two one-dimensional sequences.

Old, no conjugate, version of correlate.

uses FFT which has superior performance on large arrays.

The definition of correlation above is not unique and sometimes correlation may be defined differently. Another common definition is:

which is related to \(c_k\) by \(c’_k = c_\) .

numpy.correlate may perform slowly in large arrays (i.e. n = 1e5) because it does not use the FFT to compute the convolution; in that case, scipy.signal.correlate might be preferable.

>>> np.correlate([1, 2, 3], [0, 1, 0.5]) array([3.5]) >>> np.correlate([1, 2, 3], [0, 1, 0.5], "same") array([2. , 3.5, 3. ]) >>> np.correlate([1, 2, 3], [0, 1, 0.5], "full") array([0.5, 2. , 3.5, 3. , 0. ]) 

>>> np.correlate([1+1j, 2, 3-1j], [0, 1, 0.5j], 'full') array([ 0.5-0.5j, 1.0+0.j , 1.5-1.5j, 3.0-1.j , 0.0+0.j ]) 

Note that you get the time reversed, complex conjugated result ( \(\overline>\) ) when the two input sequences a and v change places:

>>> np.correlate([0, 1, 0.5j], [1+1j, 2, 3-1j], 'full') array([ 0.0+0.j , 3.0+1.j , 1.5+1.5j, 1.0+0.j , 0.5+0.5j]) 

Источник

Функция np.correlate() в Python — что делает

Python numpy.correlate(v1,v2, mode) выполняет свертку массива v1 с обращением массива v2 и дает результат, обрезанный с использованием одного из трех указанных режимов.

Что такое функция np.correlate() в Python?

Метод numpy.correlate() в Python используется для поиска взаимной перекрестной корреляции между двумя одномерными векторами. Функция np.correlate(), которая вычисляет корреляцию, как обычно определено в тексте с одиночной обработкой, задается как: c_ [k] = sum_n v1[n+k] * conj(v2[n]) с последовательностями v1 и v2, при необходимости дополняется нулями, а conj является сопряженным.

Синтаксис

Параметры

Функция numpy.correlate() принимает не более четырех параметров:

• v1: array_like, первый одномерный входной массив. Предположим, он имеет форму(M,)
• v2: array_like, второй одномерный входной массив. Предположим, он имеет форму(N,)
• mode: . Это необязательный параметр, который имеет три различных режима, которые поясняются ниже:

1. «valid»: это режим по умолчанию. Режим «действителен» возвращает вывод длины max(M, N) – min(M, N) + 1. Продукт свертки дается только тогда, когда v1 и v2 полностью перекрывают друг друга. Значения вне границы сигнала не влияют.
2. «same»: возвращает выходные данные длины min(M, N). Пограничные эффекты все еще видны.
3. «full»: это возвращает свертку в каждой точке перекрытия с выходной формой(M + N-1). В конечных точках свертки векторы v1 и v2 не перекрываются полностью, и могут наблюдаться граничные эффекты.

• ‘old_behavior: bool, это логический параметр, который может принимать значения true или false.

В случае, если old_behavoiur принимает значение true из числового значения(correlate(v1, v2) == correct(v2, v1), сопряжение не берется для сложных массивов. В противном случае, если old_behavoiur принимает значение false из числового значения, тогда используется обычное определение обработки сигналов.

Возвращаемое значение

Метод numpy.correlate() возвращает взаимную корреляцию одномерных векторов v1 и v2.

Примеры программ с функцией numpy.correlate()

Пример 1

Программа для демонстрации работы метода numpy.correlate():

Источник

scipy.signal.correlate#

Cross-correlate in1 and in2, with the output size determined by the mode argument.

Parameters : in1 array_like

in2 array_like

Second input. Should have the same number of dimensions as in1.

mode str , optional

A string indicating the size of the output:

The output is the full discrete linear cross-correlation of the inputs. (Default)

The output consists only of those elements that do not rely on the zero-padding. In ‘valid’ mode, either in1 or in2 must be at least as large as the other in every dimension.

The output is the same size as in1, centered with respect to the ‘full’ output.

method str , optional

A string indicating which method to use to calculate the correlation.

The correlation is determined directly from sums, the definition of correlation.

The Fast Fourier Transform is used to perform the correlation more quickly (only available for numerical arrays.)

Automatically chooses direct or Fourier method based on an estimate of which is faster (default). See convolve Notes for more detail.

An N-dimensional array containing a subset of the discrete linear cross-correlation of in1 with in2.

contains more documentation on method.

calculates the lag / displacement indices array for 1D cross-correlation.

The correlation z of two d-dimensional arrays x and y is defined as:

z[. ,k,. ] = sum[. , i_l, . ] x[. , i_l,. ] * conj(y[. , i_l - k,. ]) 

This way, if x and y are 1-D arrays and z = correlate(x, y, ‘full’) then

where \(||x||\) is the length of x , \(N = \max(||x||,||y||)\) , and \(y_m\) is 0 when m is outside the range of y.

method=’fft’ only works for numerical arrays as it relies on fftconvolve . In certain cases (i.e., arrays of objects or when rounding integers can lose precision), method=’direct’ is always used.

When using “same” mode with even-length inputs, the outputs of correlate and correlate2d differ: There is a 1-index offset between them.

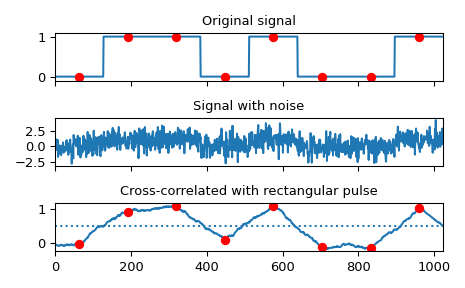
Implement a matched filter using cross-correlation, to recover a signal that has passed through a noisy channel.

>>> import numpy as np >>> from scipy import signal >>> import matplotlib.pyplot as plt >>> rng = np.random.default_rng() 

>>> sig = np.repeat([0., 1., 1., 0., 1., 0., 0., 1.], 128) >>> sig_noise = sig + rng.standard_normal(len(sig)) >>> corr = signal.correlate(sig_noise, np.ones(128), mode='same') / 128 

>>> clock = np.arange(64, len(sig), 128) >>> fig, (ax_orig, ax_noise, ax_corr) = plt.subplots(3, 1, sharex=True) >>> ax_orig.plot(sig) >>> ax_orig.plot(clock, sig[clock], 'ro') >>> ax_orig.set_title('Original signal') >>> ax_noise.plot(sig_noise) >>> ax_noise.set_title('Signal with noise') >>> ax_corr.plot(corr) >>> ax_corr.plot(clock, corr[clock], 'ro') >>> ax_corr.axhline(0.5, ls=':') >>> ax_corr.set_title('Cross-correlated with rectangular pulse') >>> ax_orig.margins(0, 0.1) >>> fig.tight_layout() >>> plt.show() 

Compute the cross-correlation of a noisy signal with the original signal.

>>> x = np.arange(128) / 128 >>> sig = np.sin(2 * np.pi * x) >>> sig_noise = sig + rng.standard_normal(len(sig)) >>> corr = signal.correlate(sig_noise, sig) >>> lags = signal.correlation_lags(len(sig), len(sig_noise)) >>> corr /= np.max(corr) 

>>> fig, (ax_orig, ax_noise, ax_corr) = plt.subplots(3, 1, figsize=(4.8, 4.8)) >>> ax_orig.plot(sig) >>> ax_orig.set_title('Original signal') >>> ax_orig.set_xlabel('Sample Number') >>> ax_noise.plot(sig_noise) >>> ax_noise.set_title('Signal with noise') >>> ax_noise.set_xlabel('Sample Number') >>> ax_corr.plot(lags, corr) >>> ax_corr.set_title('Cross-correlated signal') >>> ax_corr.set_xlabel('Lag') >>> ax_orig.margins(0, 0.1) >>> ax_noise.margins(0, 0.1) >>> ax_corr.margins(0, 0.1) >>> fig.tight_layout() >>> plt.show() 

Источник