Vectors in python examples

Работа с векторами в Python с помощью NumPy

В этом уроке мы узнаем, как создать вектор с помощью библиотеки Numpy в Python. Мы также рассмотрим основные операции с векторами, такие как сложение, вычитание, деление и умножение двух векторов, векторное точечное произведение и векторное скалярное произведение.

Что такое вектор в Python?

Вектор известен как одномерный массив. Вектор в Python – это единственный одномерный массив списков, который ведет себя так же, как список Python. Согласно Google, вектор представляет направление, а также величину; особенно он определяет положение одной точки в пространстве относительно другой.

Векторы очень важны в машинном обучении, потому что у них есть величина, а также особенности направления. Давайте разберемся, как мы можем создать вектор на Python.

Создание вектора в Python

Модуль Python Numpy предоставляет метод numpy.array(), который создает одномерный массив, то есть вектор. Вектор может быть горизонтальным или вертикальным.

Вышеупомянутый метод принимает список в качестве аргумента и возвращает numpy.ndarray.

Давайте разберемся в следующих примерах.

Пример – 1: горизонтальный вектор

# Importing numpy import numpy as np # creating list list1 = [10, 20, 30, 40, 50] # Creating 1-D Horizontal Array vtr = np.array(list1) vtr = np.array(list1) print("We create a vector from a list:") print(vtr)

We create a vector from a list: [10 20 30 40 50]

Пример – 2: Вертикальный вектор

# Importing numpy import numpy as np # defining list list1 = [[12], [40], [6], [10]] # Creating 1-D Vertical Array vtr = np.array(list1) vtr = np.array(list1) print("We create a vector from a list:") print(vtr)

We create a vector from a list: [[12] [40] [ 6] [10]]

Базовые операции вектора Python

После создания вектора мы теперь будем выполнять арифметические операции над векторами.

Ниже приведен список основных операций, которые мы можем производить с векторами:

• сложение;
• вычитание;
• умножение;
• деление;
• точечное произведение;
• скалярные умножения.

Сложение двух векторов

В векторном сложении это происходит поэлементно, что означает, что сложение будет происходить поэлементно, а длина будет такой же, как у двух аддитивных векторов.

Давайте разберемся в следующем примере.

import numpy as np list1 = [10,20,30,40,50] list2 = [11,12,13,14,15] vtr1 = np.array(list1) vtr2= np.array(list2) print("We create vector from a list 1:") print(vtr1) print("We create vector from a list 2:") print(vtr2) vctr_add = vctr1+vctr2 print("Addition of two vectors: ",vtr_add)

We create vector from a list 1: [10 20 30 40 50] We create vector from a list 2: [11 12 13 14 15] Addition of two vectors: [21 32 43 54 65]

Вычитание

Вычитание векторов выполняется так же, как и сложение, оно следует поэлементному подходу, и элементы вектора 2 будут вычтены из вектора 1. Давайте разберемся в следующем примере.

import numpy as np list1 = [10,20,30,40,50] list2 = [5,2,4,3,1] vtr1 = np.array(list1) vtr2= np.array(list2) print("We create vector from a list 1:") print(vtr1) print("We create a vector from a list 2:") print(vtr2) vtr_sub = vtr1-vtr2 print("Subtraction of two vectors: ",vtr_sub)

We create vector from a list 1: [10 20 30 40 50] We create vector from a list 2: [5 2 4 3 1] Subtraction of two vectors: [5 18 26 37 49]

Умножение векторов

Элементы вектора 1 умножаются на вектор 2 и возвращают векторы той же длины, что и векторы умножения.

import numpy as np list1 = [10,20,30,40,50] list2 = [5,2,4,3,1] vtr1 = np.array(list1) vtr2= np.array(list2) print("We create vector from a list 1:") print(vtr1) print("We create a vector from a list 2:") print(vtr2) vtr_mul = vtr1*vtr2 print("Multiplication of two vectors: ",vtr_mul)

We create vector from a list 1: [10 20 30 40 50] We create vector from a list 2: [5 2 4 3 1] Multiplication of two vectors: [ 50 40 120 120 50]

Умножение производится следующим образом.

vct[0] = x[0] * y[0] vct[1] = x[1] * y[1]

Первый элемент вектора 1 умножается на первый элемент соответствующего вектора 2 и так далее.

Операция деления двух векторов

В операции деления результирующий вектор содержит значение частного, полученное при делении двух элементов вектора.

Давайте разберемся в следующем примере.

import numpy as np list1 = [10,20,30,40,50] list2 = [5,2,4,3,1] vtr1 = np.array(list1) vtr2= np.array(list2) print("We create vector from a list 1:") print(vtr1) print("We create a vector from a list 2:") print(vtr2) vtr_div = vtr1/vtr2 print("Division of two vectors: ",vtr_div)

We create vector from a list 1: [10 20 30 40 50] We create vector from a list 2: [5 2 4 3 1] Division of two vectors: [ 2. 10. 7.5 13.33333333 50. ]

Как видно из вышеприведенного вывода, операция деления вернула частное значение элементов.

Векторное точечное произведение

Векторное скалярное произведение выполняется между двумя последовательными векторами одинаковой длины и возвращает единичное скалярное произведение. Мы будем использовать метод .dot() для выполнения скалярного произведения. Это произойдет, как показано ниже.

vector c = x . y =(x1 * y1 + x2 * y2)

Давайте разберемся в следующем примере.

import numpy as np list1 = [10,20,30,40,50] list2 = [5,2,4,3,1] vtr1 = np.array(list1) vtr2= np.array(list2) print("We create vector from a list 1:") print(vtr1) print("We create a vector from a list 2:") print(vtr2) vtr_product = vtr1.dot(vtr2) print("Dot product of two vectors: ",vtr_product)

We create vector from a list 1: [10 20 30 40 50] We create vector from a list 2: [5 2 4 3 1] Dot product of two vectors: 380

Векторно-скалярное умножение

В операции скалярного умножения; мы умножаем скаляр на каждую компоненту вектора. Давайте разберемся в следующем примере.

import numpy as np list1 = [10,20,30,40,50] vtr1 = np.array(list1) scalar_value = 5 print("We create vector from a list 1:") print(vtr1) # printing scalar value print("Scalar Value : " + str(scalar_value)) vtr_scalar = vtr1 * scalar_value print("Multiplication of two vectors: ",vtr_scalar)

We create vector from a list 1: [10 20 30 40 50] Scalar Value : 5 Multiplication of two vectors: [ 50 100 150 200 250]

В приведенном выше коде скалярное значение умножается на каждый элемент вектора в порядке s * v =(s * v1, s * v2, s * v3).

Источник

Vectorization in Python

We know that most of the application has to deal with a large number of datasets. Hence, a non-computationally-optimal function can become a huge bottleneck in your algorithm and can take result in a model that takes ages to run. To make sure that the code is computationally efficient, we will use vectorization.

Time complexity in the execution of any algorithm is very crucial deciding whether an application is reliable or not. To run a large algorithm in as much as optimal time possible is very important when it comes to real-time application of output. To do so, Python has some standard mathematical functions for fast operations on entire arrays of data without having to write loops. One of such library which contains such function is numpy. Let’s see how can we use this standard function in case of vectorization.

What is Vectorization ?
Vectorization is used to speed up the Python code without using loop. Using such a function can help in minimizing the running time of code efficiently. Various operations are being performed over vector such as dot product of vectors which is also known as scalar product as it produces single output, outer products which results in square matrix of dimension equal to length X length of the vectors, Element wise multiplication which products the element of same indexes and dimension of the matrix remain unchanged.

We will see how the classic methods are more time consuming than using some standard function by calculating their processing time.

outer(a, b): Compute the outer product of two vectors.
multiply(a, b): Matrix product of two arrays.
dot(a, b): Dot product of two arrays.
zeros((n, m)): Return a matrix of given shape and type, filled with zeros.
process_time(): Return the value (in fractional seconds) of the sum of the system and user CPU time of the current process. It does not include time elapsed during sleep.

Dot Product:
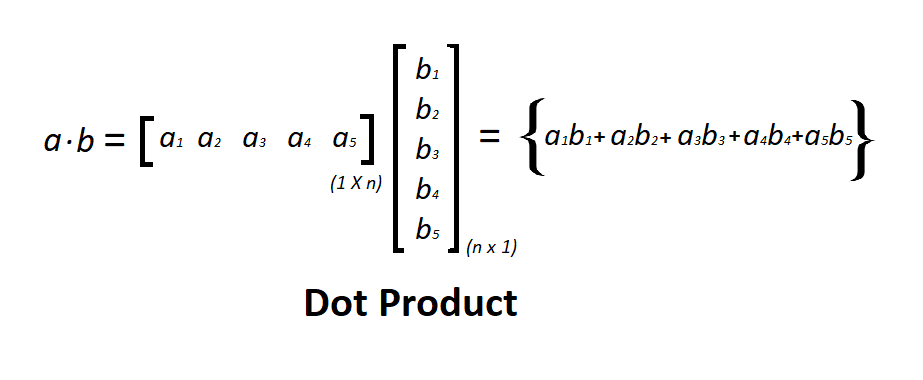
Dot product is an algebraic operation in which two equal length vectors are being multiplied such that it produces a single number. Dot Product often called as inner product. This product results in a scalar number. Let’s consider two matrix a and b of same length, the dot product is done by taking the transpose of first matrix and then mathematical matrix multiplication of a’(transpose of a) and b is followed as shown in the figure below.

Pictorial representation of dot product –

Источник