Validate binary search tree java

Validating a Binary Search Tree

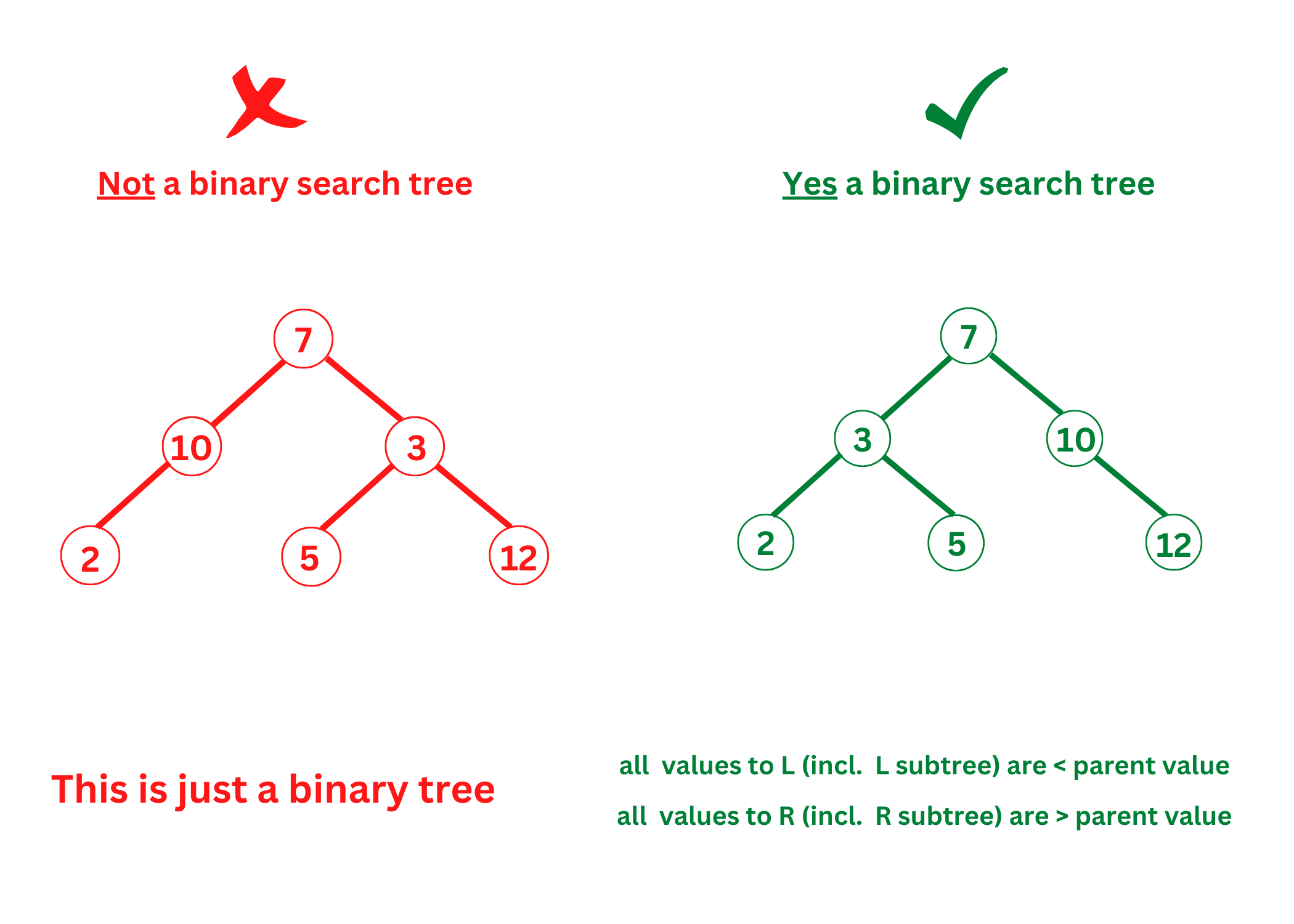
the key in any node is larger than the keys in all nodes in that node’s left subtree and smaller than the keys in all nodes in that node’s right sub-tree

public class BinarySearchTree < private Node root; private static class Node < private Integer value; private Node left; private Node right; Node(Integer value) < this.value = value; >> /** * Returns true if 'tree' is a binary search tree, false otherwise. */ public static boolean isBinarySearchTree(BinarySearchTree tree) < return isBinarySearchTree(tree.root, null, null); >private static boolean isBinarySearchTree(Node root, Integer min, Integer max) < if (root != null) < Integer value = (Integer) root.value; if (root.left != null) < Integer left = (Integer) root.left.value; if (!(value >left && (min == null || left > min) && (max == null || left < max) && isBinarySearchTree(root.left, min, value))) < return false; >> if (root.right != null) < Integer right = (Integer) root.right.value; if (!(value < right && (min == null || right >min) && (max == null || right < max) && isBinarySearchTree(root.right, value, max))) < return false; >> > return true; > /** * Builds a BinarySearchTree from an in-order array representation. * Assumes the tree is complete at each level. */ public static BinarySearchTree fromArray(Integer[] repr) < BinarySearchTree tree = new BinarySearchTree(); tree.root = fromArray(repr, 0, repr.length - 1); return tree; >private static Node fromArray(Integer[] repr, int start, int end) < if (start >end) < return null; >int m = start + ((end - start) / 2); Node n = new Node(repr[m]); n.left = fromArray(repr, start, m - 1); n.right = fromArray(repr, m + 1, end); return n; > /** * Returns an in-order array representation of the tree. */ public Integer[] toArray() < return toList(root).toArray(new Integer[]<>); > private List toList(Node n) < ArrayListvalues = new ArrayList<>(); if (n != null) < values.addAll(0, toList(n.left)); values.add(n.value); values.addAll(toList(n.right)); >return values; > > 

public static void main(String[] args) < Integer[] arrayRepr = null; BinarySearchTree tree = null; arrayRepr = new Integer[] <>; tree = BinarySearchTree.fromArray(arrayRepr); assert(BinarySearchTree.isBinarySearchTree(tree)); arrayRepr = new Integer[] ; tree = BinarySearchTree.fromArray(arrayRepr); assert(BinarySearchTree.isBinarySearchTree(tree)); arrayRepr = new Integer[] ; tree = BinarySearchTree.fromArray(arrayRepr); assert(false == BinarySearchTree.isBinarySearchTree(tree)); arrayRepr = new Integer[] ; tree = BinarySearchTree.fromArray(arrayRepr); assert(BinarySearchTree.isBinarySearchTree(tree)); arrayRepr = new Integer[] ; tree = BinarySearchTree.fromArray(arrayRepr); assert(BinarySearchTree.isBinarySearchTree(tree)); arrayRepr = new Integer[] ; tree = BinarySearchTree.fromArray(arrayRepr); assert(BinarySearchTree.isBinarySearchTree(tree)); arrayRepr = new Integer[] ; tree = BinarySearchTree.fromArray(arrayRepr); assert(false == BinarySearchTree.isBinarySearchTree(tree)); arrayRepr = new Integer[] ; tree = BinarySearchTree.fromArray(arrayRepr); assert(false == BinarySearchTree.isBinarySearchTree(tree)); > 

Источник

LeetCode – Validate Binary Search Tree (Java)

Given a binary tree, determine if it is a valid binary search tree (BST).

Assume a BST is defined as follows:

• The left subtree of a node contains only nodes with keys less than the node’s key.
• The right subtree of a node contains only nodes with keys greater than the node’s key.
• Both the left and right subtrees must also be binary search trees.

Java Solution 1 — Recursive

All values on the left sub tree must be less than parent and parent’s parent, and all values on the right sub tree must be greater than parent and parent’s parent. So we just check the boundaries for each node.

public boolean isValidBST(TreeNode root) { return isValidBST(root, Double.NEGATIVE_INFINITY, Double.POSITIVE_INFINITY); } public boolean isValidBST(TreeNode p, double min, double max)

This solution also goes to the left subtree first. If the violation occurs close to the root but on the right subtree, the method still cost time O(n) and space O(h).

The following solution can handle violations close to root node faster.

public boolean isValidBST(TreeNode root) { return helper(root, Double.NEGATIVE_INFINITY, Double.POSITIVE_INFINITY); } public boolean helper(TreeNode root, double min, double max){ if(root==null){ return true; } if(root.valmin||root.val>=max){ return false; } boolean isLeftBST = helper(root.left, min, root.val); boolean isRightBST = helper(root.right, root.val, max); if(!isLeftBST||!isRightBST){ return false; } return true; }

public boolean isValidBST(TreeNode root) < return helper(root, Double.NEGATIVE_INFINITY, Double.POSITIVE_INFINITY); >public boolean helper(TreeNode root, double min, double max) < if(root==null)< return true; >if(root.val<=min||root.val>=max) < return false; >boolean isLeftBST = helper(root.left, min, root.val); boolean isRightBST = helper(root.right, root.val, max); if(!isLeftBST||!isRightBST) < return false; >return true; >

Java Solution 2 — Iterative

public class Solution  if(b.n.left!=null){ queue.offer(new BNode(b.n.left, b.left, b.n.val)); } if(b.n.right!=null){ queue.offer(new BNode(b.n.right, b.n.val, b.right)); } } return true; } } //define a BNode class with TreeNode and it's boundaries class BNode{ TreeNode n; double left; double right; public BNode(TreeNode n, double left, double right){ this.n = n; this.left = left; this.right = right; } }

Time and space are both O(n).

Java Solution 3 — In-order traversal

Since inorder traversal of BST is ascending, so we can check the sequence. Time is O(n) and space is O(h). h is the height of the stack which is the tree’s height.

Related posts:

If you want someone to read your code, please put the code inside

 and 

tags. For example:

private static boolean isBST(Node root, int minValue, int maxValue) < if(root==null)
return true;
if(root.data=maxValue)
return false;
return isBST(root.left, minValue, root.data)
&& isBST(root.right, root.data, maxValue);
>

class Solution <
public boolean isValidBST(TreeNode root) <
return isBST(root, Double.NEGATIVE_INFINITY, Double.POSITIVE_INFINITY);
>
public boolean isBST(TreeNode tree, double min, double max) <
if (tree == null) <
return true;
>
if(tree.val=max) <
return false;
>
return isBST(tree.left, min, tree.val) && isBST(tree.right, tree.val,max);
> >

if a value less than a parent it should be less than its parents parent. Above code will still validate that since it is recursive. Please give me an example for your UC.

The left child value needs to be not only smaller than parent, also smaller than parent’s parent value.

Источник

Validate Binary Search Tree: Check if BST or not? (Java & C++)

If you have studied DSA in your college, then you know what trees are, and how bad the questions related to them can be. The different types of trees in Data Structures can confuse anybody!

So, in today’s tech blog we are going to discuss Binary Search Trees, and how you can validate that a particularly given tree is a BST. Get ready for examples, of different methods for solving the same question along with their implementation in C++ and Java. Let’s get started, folks!

What is a BST?

A Binary Search Tree is a tree data structure that is based on nodes. It has the following properties:

• The Left sub-tree of a node contains nodes with keys less than the node’s key.
• The Right Subtree of the node contains nodes with keys greater than the node’s key.
• Both left and right subtrees should individually be Binary Search Trees.
• Each node(value in the tree) should have a distinct key.

If a given tree satisfies the above properties, it is a BST. Still confused? Look at the given illustration:

Validate BST Problem Statement

Here is the problem statement: «You are given a tree data structure. You need to check whether it is a BST or not. For checking this thing, you need to check the above 4 properties of the tree individually.»

In short, we have to validate a binary search tree.

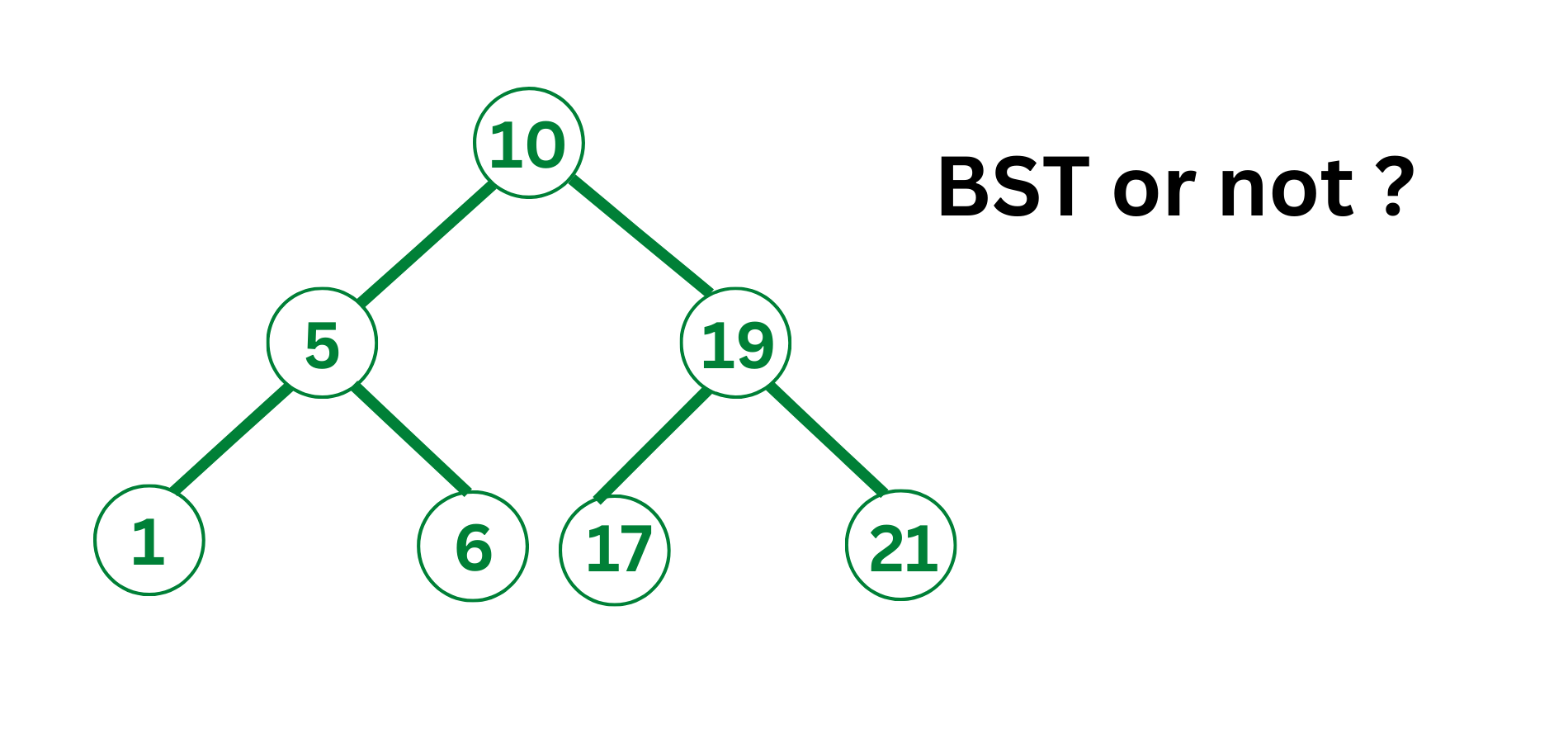
Example

Look at the given image to see what the problem is.

03 Methods to Validate Binary Search Tree

Although the question is the same, we still have like 3 methods for you to solve this!

Method 01) Naive Approach

The following steps need to be followed for this approach:

1. Check whether the node is single or not. If yes, return True.
2. Traverse every node in the left subtree, and check whether each value is less than the root’s value.
3. Traverse every node in the right subtree, and check whether each value is bigger than the root’s value.
4. If a node in the left subtree is found to have a bigger value than the root, Return False.
5. If a node in the right subtree is found to have a smaller value than the root, Return False.
6. Keep checking whether both the left and right subtrees of the root are also BST.
7. If yes, return True.

Method 02) Using Upper & Lower Limits

For implementing this method, follow the given steps:

1. If currentNode == NULL, return True.
2. If LowerLimit is not equal to NULL and the value at CurrentNode
3. If UpperLimit is not equal to NULL and the value at CurrentNode >= UpperLimit, return False.
4. Keep checking whether the left subtree of CurrentNode is BST or not, along with the value of CurrentNode as UpperLimit and LowerLimit as the lower limit.
5. If the left subtree is not BST, return False.
6. Keep checking whether the right subtree of CurrentNode is BST or not, along with the value of CurrentNode as LowerLimit and UpperLimit as the upper limit.
7. If the right subtree is not BST, return False. Else, return True.

Method 03) Using Inorder Traversal

How can an Inorder Traversal validate a BST? Well, this is because if on traversing a tree in an inorder fashion, it gives a Sorted array of tree values, then it is a Binary Search Tree. Let’s take a deeper look at this!

If the in-order traversal of a tree returns a sorted array of elements, then it is quite obvious that the right and left subtrees of the tree will also give sorted elements. Why? This is because the Inorder Traversal of a tree always traverses the Left Subtree, then the root, and later the Right Subtree. Now, this means that every node value in Left Subtree should be smaller than the root’s value, and that also means that every node value in the right subtree must be greater than the root’s value.

Now, this in-order traversal method can be improved by observing that we don’t have to store every node value. We can just check if the previous element in the tree traversal is less than the current element.

Code Implementation in C++

Here is the C++ code to validate BST:

#include  using namespace std; struct node < int data; struct node* left; struct node* right; >; struct node* newNode(int data) < struct node* node = (struct node*)malloc(sizeof(struct node)); node->data = data; node->left = NULL; node->right = NULL; return (node); > int maxValue(struct node* node) < if (node == NULL) < return INT16_MIN; > int value = node->data; int leftMax = maxValue(node->left); int rightMax = maxValue(node->right); return max(value, max(leftMax, rightMax)); > int minValue(struct node* node) < if (node == NULL) < return INT16_MAX; > int value = node->data; int leftMax = minValue(node->left); int rightMax = minValue(node->right); return min(value, min(leftMax, rightMax)); > int isBST(struct node* node) < if (node == NULL) return 1; if (node->left != NULL && maxValue(node->left) > node->data) return 0; if (node->right != NULL && minValue(node->right) < node->data) return 0; if (!isBST(node->left) || !isBST(node->right)) return 0; return 1; > int main() < struct node* root = newNode(4); root->left = newNode(2); root->right = newNode(5); root->left->left = newNode(1); root->left->right = newNode(3); if (isBST(root)) printf("Is BST"); else printf("Not a BST"); return 0; >

Code Implementation in Java

Here is the Java code to validate BST:

import java.io.*; class Solution < static class node < int data; node left, right; > static node newNode(int info) < node Node = new node(); Node.info = info; Node.left = Node.right = null; return Node; > static int Value(node Node) < if (Node == null) < return Integer.MIN_VALUE; > int value = Node.data; int leftMax = Value(Node.left); int rightMax = Value(Node.right); return Math.max(value, Math.max(leftMax, rightMax)); > static int minValue(node Node) < if (Node == null) < return Integer.MAX_VALUE; > int value = Node.data; int leftMax = minValue(Node.left); int rightMax = minValue(Node.right); return Math.min(value, Math.min(leftMax, rightMax)); > 
static int BST(node Node) < if (Node == null) < return 1; > if (Node.left != null && maxValue(Node.left) > Node.data) < return 0; > if (Node.right != null && minValue(Node.right) < Node.data) < return 0; > if (isBST(Node.left) != 1 || isBST(Node.right) != 1) < return 0; > return 1; > public static void main(String[] args) < node root = newNode(4); root.left = newNode(2); root.right = newNode(5); root.left.left = newNode(1); root.left.right = newNode(3); if (BST(root) == 1) < System.out.print("Is BST"); > else < System.out.print("Not a BST"); > > >

Conclusion

So, in this tech blog, we came up with 3 different solutions to validate a Binary Search Tree. Although each solution is good on its own, the last one, that is, the inorder traversal of trees is the best to use in practice. For more such tech blogs on complex topics, you can always rely on FavTutor!

Источник