Python — Binary Tree
We create a tree data structure in python by using the concept os node discussed earlier. We designate one node as root node and then add more nodes as child nodes. Below is program to create the root node.
Create Root
We just create a Node class and add assign a value to the node. This becomes tree with only a root node.
Example
class Node: def __init__(self, data): self.left = None self.right = None self.data = data def PrintTree(self): print(self.data) root = Node(10) root.PrintTree()
Output
When the above code is executed, it produces the following result −
Inserting into a Tree
To insert into a tree we use the same node class created above and add a insert class to it. The insert class compares the value of the node to the parent node and decides to add it as a left node or a right node. Finally the PrintTree class is used to print the tree.
Example
class Node: def __init__(self, data): self.left = None self.right = None self.data = data def insert(self, data): # Compare the new value with the parent node if self.data: if data < self.data: if self.left is None: self.left = Node(data) else: self.left.insert(data) elif data >self.data: if self.right is None: self.right = Node(data) else: self.right.insert(data) else: self.data = data # Print the tree def PrintTree(self): if self.left: self.left.PrintTree() print( self.data), if self.right: self.right.PrintTree() # Use the insert method to add nodes root = Node(12) root.insert(6) root.insert(14) root.insert(3) root.PrintTree()
Output
When the above code is executed, it produces the following result −
Traversing a Tree
The tree can be traversed by deciding on a sequence to visit each node. As we can clearly see we can start at a node then visit the left sub-tree first and right sub-tree next. Or we can also visit the right sub-tree first and left sub-tree next. Accordingly there are different names for these tree traversal methods.
Tree Traversal Algorithms
Traversal is a process to visit all the nodes of a tree and may print their values too. Because, all nodes are connected via edges (links) we always start from the root (head) node. That is, we cannot randomly access a node in a tree. There are three ways which we use to traverse a tree.
In-order Traversal
In this traversal method, the left subtree is visited first, then the root and later the right sub-tree. We should always remember that every node may represent a subtree itself.
In the below python program, we use the Node class to create place holders for the root node as well as the left and right nodes. Then, we create an insert function to add data to the tree. Finally, the In-order traversal logic is implemented by creating an empty list and adding the left node first followed by the root or parent node.
At last the left node is added to complete the In-order traversal. Please note that this process is repeated for each sub-tree until all the nodes are traversed.
Example
class Node: def __init__(self, data): self.left = None self.right = None self.data = data # Insert Node def insert(self, data): if self.data: if data < self.data: if self.left is None: self.left = Node(data) else: self.left.insert(data) else data >self.data: if self.right is None: self.right = Node(data) else: self.right.insert(data) else: self.data = data # Print the Tree def PrintTree(self): if self.left: self.left.PrintTree() print( self.data), if self.right: self.right.PrintTree() # Inorder traversal # Left -> Root -> Right def inorderTraversal(self, root): res = [] if root: res = self.inorderTraversal(root.left) res.append(root.data) res = res + self.inorderTraversal(root.right) return res root = Node(27) root.insert(14) root.insert(35) root.insert(10) root.insert(19) root.insert(31) root.insert(42) print(root.inorderTraversal(root))
Output
When the above code is executed, it produces the following result −
Pre-order Traversal
In this traversal method, the root node is visited first, then the left subtree and finally the right subtree.
In the below python program, we use the Node class to create place holders for the root node as well as the left and right nodes. Then, we create an insert function to add data to the tree. Finally, the Pre-order traversal logic is implemented by creating an empty list and adding the root node first followed by the left node.
At last, the right node is added to complete the Pre-order traversal. Please note that, this process is repeated for each sub-tree until all the nodes are traversed.
Example
class Node: def __init__(self, data): self.left = None self.right = None self.data = data # Insert Node def insert(self, data): if self.data: if data < self.data: if self.left is None: self.left = Node(data) else: self.left.insert(data) elif data >self.data: if self.right is None: self.right = Node(data) else: self.right.insert(data) else: self.data = data # Print the Tree def PrintTree(self): if self.left: self.left.PrintTree() print( self.data), if self.right: self.right.PrintTree() # Preorder traversal # Root -> Left ->Right def PreorderTraversal(self, root): res = [] if root: res.append(root.data) res = res + self.PreorderTraversal(root.left) res = res + self.PreorderTraversal(root.right) return res root = Node(27) root.insert(14) root.insert(35) root.insert(10) root.insert(19) root.insert(31) root.insert(42) print(root.PreorderTraversal(root))
Output
When the above code is executed, it produces the following result −
Post-order Traversal
In this traversal method, the root node is visited last, hence the name. First, we traverse the left subtree, then the right subtree and finally the root node.
In the below python program, we use the Node class to create place holders for the root node as well as the left and right nodes. Then, we create an insert function to add data to the tree. Finally, the Post-order traversal logic is implemented by creating an empty list and adding the left node first followed by the right node.
At last the root or parent node is added to complete the Post-order traversal. Please note that, this process is repeated for each sub-tree until all the nodes are traversed.
Example
class Node: def __init__(self, data): self.left = None self.right = None self.data = data # Insert Node def insert(self, data): if self.data: if data < self.data: if self.left is None: self.left = Node(data) else: self.left.insert(data) else if data >self.data: if self.right is None: self.right = Node(data) else: self.right.insert(data) else: self.data = data # Print the Tree def PrintTree(self): if self.left: self.left.PrintTree() print( self.data), if self.right: self.right.PrintTree() # Postorder traversal # Left ->Right -> Root def PostorderTraversal(self, root): res = [] if root: res = self.PostorderTraversal(root.left) res = res + self.PostorderTraversal(root.right) res.append(root.data) return res root = Node(27) root.insert(14) root.insert(35) root.insert(10) root.insert(19) root.insert(31) root.insert(42) print(root.PostorderTraversal(root))
Output
When the above code is executed, it produces the following result −
python tree
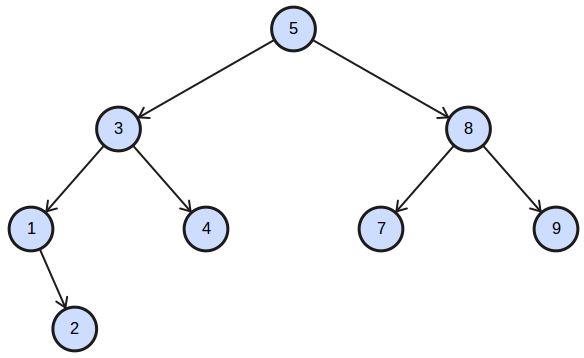
In computer science, a tree is a data structure that is modeled after nature. Unlike trees in nature, the tree data structure is upside down: the root of the tree is on top. A tree consists of nodes and its connections are called edges. The bottom nodes are also named leaf nodes. A tree may not have a cycle.
A tree with eight nodes. The root of the tree (5) is on top.
Python does not have built-in support for trees.
Binary tree
A binary tree is a data structure where every node has at most two children (left and right child). The root of a tree is on top. Every node below has a node above known as the parent node.We define a class thee which has a left and right attribute. From this binary tree we define the root (top of the three) and a left and right node.
#!/usr/bin/env python
class Tree(object):
def __init__(self):
self.left = None
self.right = None
self.data = None
root = Tree()
root.data = «root»
root.left = Tree()
root.left.data = «left»
root.right = Tree()
root.right.data = «right»
print(root.left.data)
You could then further create the tree like this:
#!/usr/bin/env python
class Tree(object):
def __init__(self):
self.left = None
self.right = None
self.data = None
root = Tree()
root.data = «root»
root.left = Tree()
root.left.data = «left»
root.right = Tree()
root.right.data = «right»
root.left.left = Tree()
root.left.left.data = «left 2»
root.left.right = Tree()
root.left.right.data = «left-right»