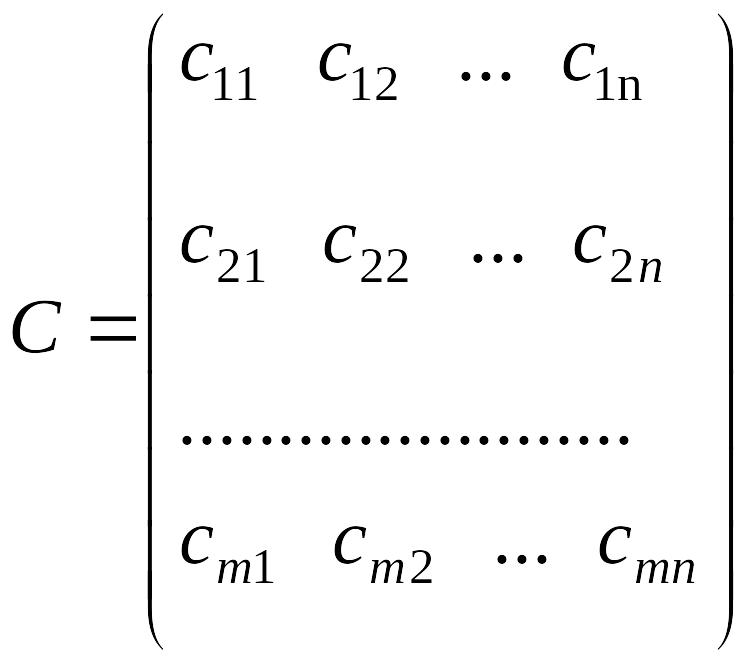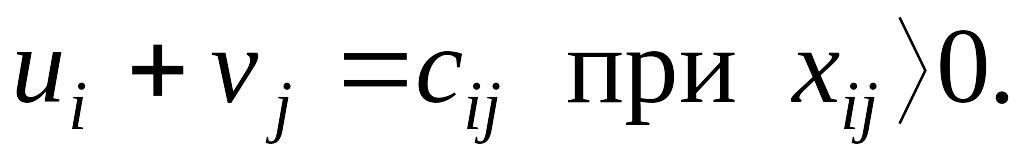Глава2 ТРАНСПОРТНАЯ ЗАДАЧА
Под транспортной задачей в дальнейшем понимается задача линейного программирования, в которой требуется найти оптимальный (по стоимости) план перевозок некоторого однородного груза от конечного числа поставщиков A 1 , A 2 , , A m с заданными запасами a 1 , , a m к конечному числу потребителей B 1 , B 2 , , B n с потребностями b 1 , , b n . Стоимость c ij перевозки единицы груза от поставщика A i к потребителю B j предполагается известной. Отметим, что данная постановка задачи может быть значительно расширена или изменена. Например, в приложениях часто рассматриваются задачи перевозки неоднородного груза. Также в качестве критерия оптимальности можно рассматривать время перевозок (транспортная задача по критерию времени). Подобного рода задачи решаются сведением к однородной транспортной задаче, или для них разработаны другие методы, изложение которых остается за рамками данной книги.
§ 2.1. Постановка задачи
Итак, пусть X = ( x ij ) – m × n матрица, где x ij – объем перевозок от i -го поставщика к j -му потребителю. Тогда общие затраты на пе-
| m | n | |
| ревозку груза определяются функцией | z ( X ) = ∑∑ c ij x ij . Математиче- | |
| i = 1 | j = 1 | |
ская постановка транспортной задачи определяется следующей задачей линейного программирования m n z ( X ) = ∑∑ c ij x ij → min i = 1 j = 1 при условиях
| ∑ x ij = b j , | j = 1, , n , | |
| m | ||
| i = 1 | ||
| n | i = 1, , m , | (2.1) |
| ∑ x ij = a i , | ||
| j = 1 | ||
| x | ≥ 0. | |
| ij | ||
Первая часть нетривиальных ограничений означает, что все потребности удовлетворены, вторая часть – то, что весь груз вывезен от поставщиков. Замечание 2.1. Если запасы и потребности задаются целыми числами, то транспортная задача имеет целочисленное оптимальное решение, поэтому транспортную задачу относят формально к задачам целочисленного линейного программирования. Можно показать, что число базисных переменных в системе ограничений (2.1) равно m + n − 1 .
| Поставщики | Потребители | Запасы | |||||
| B 1 | B 2 | … | B j | … | B n | ||
| A 1 | c 11 | c 12 | … | c 1 j | … | c 1 n | a 1 |
| x 11 | x 12 | x 1 j | x 1 n | ||||
| A | c | с | … | с | … | c | a |
| 2 | 21 | 22 | 2 j | 2 n | 2 | ||
| x 21 | x 22 | x 2 j | x 2 n | ||||
| … | … | … | … | … | … | … | … |
| A i | c i 1 | c i 2 | … | c ij | … | c in | a i |
| x i 1 | x i 2 | x ij | x in | ||||
| … | … | … | … | … | … | … | … |
| A m | c m 1 | c m 2 | … | c mj | … | c mn | a m |
| x m 1 | x m 2 | x mj | x mn | ||||
| Потребности | b 1 | b 2 | … | b j | … | b n | |
| Таблица 2.1 | |||||||
Определение 2.1. Решение X = ( x ij ) (оптимальное решение X * = ( x ij * ) ) транспортной задачи, удовлетворяющее условиям (2.1) и имеющее не более m + n − 1 занятой клетки (ненулевой перевозки), бу- дем называть опорным планом (оптимальным опорным планом) транспортной задачи. Исходные данные задачи представляют в виде таблицы 2.1. m Общие запасы определяются суммой ∑ a i , а общая потребность – i = 1
n ∑ b j . Транспортная задача называется задачей с правильным балан- j = 1
| m | n | |
| сом , а ее модель закрытой , если ∑ a i | = ∑ b j , то есть суммарные запа- | |
| i = 1 | j = 1 | |
| сы | поставщиков равны суммарным | запросам потребителей. Если |
| m | n | |
| ∑ a i ≠ ∑ b j , то такая задача называется задачей с неправильным ба- | ||
| i = 1 | j = 1 | |
лансом , а ее модель – открытой .
§ 2.2. Построение начального опорного плана транспортной задачи
Алгоритм решения транспортной задачи с правильным балансом излагается в курсе «Линейная алгебра». В этом параграфе мы напомним основные методы построения начального опорного плана и метод потенциалов решения транспортной задачи. Первым этапом решения является построение начального опорного плана, т.е. плана перевозок, удовлетворяющего всем ограничениям конкретной транспортной задачи. Сущность методов состоит в том, что начальный опорный план находят за не более чем m + n − 1 шагов (по числу базисных переменных), на каждом из которых в транспортной таблице заполняют одну клетку, которую называют занятой. Заполнение одной из клеток обеспечивает полностью либо удовлетворение потребности в грузе одного из пунктов назначения (того, в столбце которого находится заполненная клетка), либо вывоз груза из одного из пунктов
| B 1 | B 2 | B 3 | B 4 | a i | |
| A 1 | 1 | 11 | 3 | 13 | 140 |
| A 2 | 12 | 4 | 8 | 2 | 160 |
| A 3 | 3 | 5 | 14 | 6 | 100 |
| b j | 80 | 40 | 150 | 130 | 400 |
| Таблица 2.2 | |||||
оптимального.
отправления (из того, в строке которого находится заполняемая клетка). Различаются эти планы по принципам выбора заполняемых клеток и, в зависимости от этого, могут давать планы, более или менее отличные от
Пример 2.1. Рассмотрим транспортную задачу, заданную таблицей 2.2. В правом нижнем углу стоит сумма запасов (и, одновременно, сумма потребностей, так как модель закрытая) 140+160+100=80+40+ +150+ 130=400.
| Напомним | сначала | метод северо-западного | угла. Заполнение | |||||||
| таблицы начинаем с левого | ||||||||||
| B 1 | B 2 | B 3 | B 4 | a i | верхнего (северо-западного) | |||||
| A 1 | 1 | 40 | 11 | 3 | 13 | 140 | угла таблицы. Так как по- | |||
| 80 | 20 | |||||||||
| требности первого потреби- | ||||||||||
| A 2 | 12 | 4 | 8 | 2 | 160 | |||||
| теля В 1 равны 80, а запасы | ||||||||||
| 130 | 30 | |||||||||
| A 3 | 3 | 5 | 14 | 6 | 100 | первого поставщика A 1 | рав- | |||
| 100 | ны 140, то в клетку | A 1 B 1 | ||||||||
| b j | 80 | 40 | 150 | 130 | 400 | |||||
| вписываем | максимально | |||||||||
| Таблица 2.3 | возможную перевозку | 80. | ||||||||
| Потребности В 1 | полностью удовлетворены, поэтому первый столбец | |||||||||
исключаем из рассмотрения, а оставшиеся запасы первого поставщика, т.е. 60, переносим следующим потребителям. Мы можем 40 записать потребителю В 2 (столбец В 2 исключается), а оставшиеся 20 – В 3 и исключить первую строку из дальнейшего рассмотрения . Далее, так как потребности В 3 равны 150, а 20 единиц груза ему уже доставлены, то оставшиеся 130 единиц доставляются от второго поставщика A 2 (заполняем клетку A 2 B 3 ) . С толбец В 3 исключаем из рассмотрения, а оставшиеся запасы второго поставщика (30 единиц) записываем потребителю В 4 . Окончательно потребности последнего удовлетворяются за счет поставщика A 3 : вписываем в клетку A 3 B 4 пе- ревозку 100. Заметим, что, так как исходная задача — с правильным балансом, то потребности последнего потребителя B 4 равны запасам по- ставщика A 3 , т.е. 100. Получаем таблицу 2.3 с начальным опорным планом
| 80 | 40 | 20 | 0 |
| 0 | 0 | 130 | 30 |
| X = | . | ||
| 0 | 0 | 0 | 100 |
Суммарная стоимость перевозок равна z ( X ) = 1 80 + 11 40 + 3 20 + 8 130 + 2 30 + 6 100 = 2280. Из решения видно, что метод северо-западного угла, с одной стороны, достаточно прост с точки зрения построения, а с другой стороны, не учитывает стоимость перевозок. Поэтому опорный план, построенный методом северо-западного угла, как правило, далек от оптимального.
Построим теперь для этой же задачи начальный опорный план методом минимального тарифа. Суть этого метода состоит в том, что в клетки с наименьшими тарифами помещают максимально возможные перевозки. Итак, в таблице исходной задачи выбираем клетку с минимальным тарифом, т.е. клетку A 1 B 1 с тарифом 1 . Запасы постав- щика A 1 равны 140, а потребности В 1 – 80, поэтому в клетку A 1 B 1 вписываем максимально возможную перевозку 80, и потребителя В 1 ис- ключаем из рассмотрения. В оставшейся части таблицы выбираем минимальный тариф, т.е.
| B 1 | B 2 | B 3 | B 4 | a i | клетку A B с тарифом 2. За- | ||||
| 1 | 11 | 3 | 13 | ||||||
| A 1 | 140 | 2 | 4 | ||||||
| 80 | 60 | пасы поставщика A 2 | равны | ||||||
| A | 12 | 4 | 8 | 2 | 160 | 140, а потребности В 4 | — 130, | ||
| 2 | 30 | 130 | поэтому в клетку A 2 B 4 | запи- | |||||
| A 3 | 3 | 5 | 14 | 6 | 100 | ||||
| 10 | 90 | сываем перевозку 130 и по- | |||||||
| b j | 80 | 40 | 150 | 130 | 400 | требителя | В | исключаем из | |
| 4 | |||||||||
| Таблица 2.4 | рассмотрения. | У оставшихся | |||||||
потребителей В 2 , В 3 выбираем клетку с минимальным тарифом. Это A 1 B 3 с тарифом 3. Запасы (оставшиеся) поставщика A 1 равны 60, а по-
| требности В 3 – 150, поэтому в клетку | A 1 B 3 | записываем максимально | |||||
| возможную перевозку 60 и исключаем поставщика A 1 из дальнейшего | |||||||
| рассмотрения. Далее, аналогично в клетку | A 2 B 2 записываем 30 и ис- | ||||||
| ключаем второго поставщика. | |||||||
| В оставшиеся две клетки A 3 B 2 | и A 3 B 3 | последовательно вписыва- | |||||
| ем перевозку 10 в A 3 B 2 | и 90 в A 3 B 3 . Получаем таблицу 2.4 с начальным | ||||||
| 80 | 0 | 60 | 0 | ||||
| опорным планом X = | 0 | 30 | 0 | 130 | |||
| . Суммарная стоимость пере- | |||||||
| 0 | 10 | 90 | 0 | ||||
возок равна z ( X ) = 1 80 + 3 60 + 4 30 + 2 130 + 5 10 + 14 90 = 1950 < 2280. Таким образом, опорный план, построенный методом минимального тарифа, лучше, чем план, полученный методом северо-западного угла. Применим, наконец, к исходной задаче метод аппроксимации Фогеля. Для этого найдем разность между двумя минимальными тарифами для каждой строки и столбца таблицы и запишем их в дополнительно образованные строки и столбцы (см. таблицу 2.5). В строке A 1 минимальный тариф равен 1, а следующий за ним 3, поэтому раз- ность между ними 4-2=2; в строке A 2 минимальный тариф равен 2, а следующий за ним 4, поэтому разность между равна 2; аналогично, для строки A 3 разность между минимальным тарифом 3 и следующим за ним 5 равна 2. Итак, три двойки записываем в первый дополнительный столбец. Аналогично для столбцов разности 3-1=2, 5-4=1, 8-3=5 и 6-2=4 записываем в первую дополнительную строку. Теперь из всех разностей выбираем максимальную , т.е. 5 в столбце B 3 , и в клетку A 1 B 3 с минимальным тарифом в этом столбце записываем максимально возможную перевозку 140. При этом поставщика A 1 исключаем из рас- смотрения. Теперь аналогично вычисляем разности между оставшимися минимальными тарифами и заполняем вторые дополнительные столбец и строку, не учитывая тарифы в строке A 1 . Видим, что теперь максимальная разность получается в столбце B 1 и перевозку 80 записываем в клетку A 3 B 1 с минимальным тарифом 3 в этом столбце (первую строку мы исключили из рассмотрения). Столбец B 1 аналогично исключаем из рассмотрения. Как видно из таблицы, на следующем
| B 1 | B 2 | B 3 | B 4 | a i | Разности по строкам | ||||||
| A 1 | 1 | 11 | 3 | 13 | 140 | 2 | – | – | – | – | – |
| 140 | |||||||||||
| A 2 | 12 | 4 | 8 | 2 | 160 | 2 | 2 | 2 | 2 | 0 | – |
| 20 | 10 | 130 | |||||||||
| A 3 | 3 | 5 | 14 | 6 | 100 | 2 | 2 | 1 | 1 | 0 | 0 |
| 80 | 20 | ||||||||||
| b j | 80 | 40 | 150 | 130 | 400 | ||||||
| 2 | 1 | 5 | 4 | ||||||||
| 9 | 1 | 6 | 4 | ||||||||
| Разности | |||||||||||
| – | 1 | 6 | 4 | ||||||||
| по | |||||||||||
| – | 1 | – | 4 | ||||||||
| столбцам | |||||||||||
| – | 1 | – | – | ||||||||
| – | 0 | – | – | ||||||||
Таблица 2.5 шаге вписываем перевозку 10 в клетку A 2 B 3 и исключаем столбец B 3 , затем – максимально возможную перевозку 40 в клетку A 2 B 4 и исключаем из рассмотрения столбец B 4 . Теперь для вычисления дальнейших разностей остается единственный столбец B 2 , поэтому в качестве разностей по строкам записываем нули. Далее, в клетку A 2 B 2 записываем 20, а на последнем шаге записываем перевозку 20 в клетку A 3 B 2 . По-
5. Транспортная задача линейного программирования
Под названием «транспортная задача» объединяется широкий круг задач с единой математической моделью. Данные задачи относятся к задачам линейного программирования и могут быть решены симплексным методом. Однако матрица системы ограничений транспортной задачи настолько своеобразна, что для ее решения разработаны специальные методы. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его, получить оптимальное решение.
5.1. Формулировка транспортной задачи
Однородный груз сосредоточен у т поставщиков в объемах a1, a2,. ат. Данный груз необходимо доставить п потребителям в объемах b1, b2, . bn. Известны сij, i= 1, 2, . m, j = 1, 2, . п — стоимости перевозки единицы груза от каждого i-го поставщика каждому j-му потребителю. Требуется составить такой план перевозок, при котором запасы всех поставщиков будут вывезены полностью, запросы всех потребителей полностью удовлетворены и суммарные затраты на перевозку всех грузов минимальны.
Исходные данные транспортной задачи обычно записываются в таблице:
Исходные данные задачи могут быть представлены также в виде вектора запасов поставщиков А=(a1,a2,. ат), вектора запросов потребителей В=(b1,b2, . bn) и матрицы стоимостей
5.2. Алгоритм решения транспортной задачи методом потенциалов
Порядок решения транспортных задач методом потенциалов.
- Проверяют выполнение необходимого и достаточного условия разрешимости задачи. Если задача имеет неправильный баланс, то вводят фиктивного поставщика или потребителя с недостающими запасами или запросами и нулевыми стоимостями перевозок.
- Строят начальное опорное решение и проверяют правильность его построения, для чего подсчитывают количество занятых клеток (их должно быть т+п—1) и убеждаются в линейной независимости векторов-условий.
3.Строят систему потенциалов, соответствующих опорному решению. Для этого решают систему уравнений Для того чтобы найти частное решение системы, одному из потенциалов задают произвольно некоторое значение (чаще нуль). Остальные потенциалы однозначно определяются по формулам:
при если известен потенциал , и
при если известен потенциал .
4. Проверяют, выполняется ли условие оптимальности для свободных клеток таблицы. Для этого вычисляют оценки для всех свободных клеток по формулам и те оценки, которые больше нуля, записывают в левые нижние углы клеток. Если для всех свободных клеток < 0, то вычисляют значение целевой функции, и решение задачи заканчивается, так как полученное решение является оптимальным. Если же имеется хотя бы одна клетка с положительной оценкой, то опорное решение не является оптимальным.
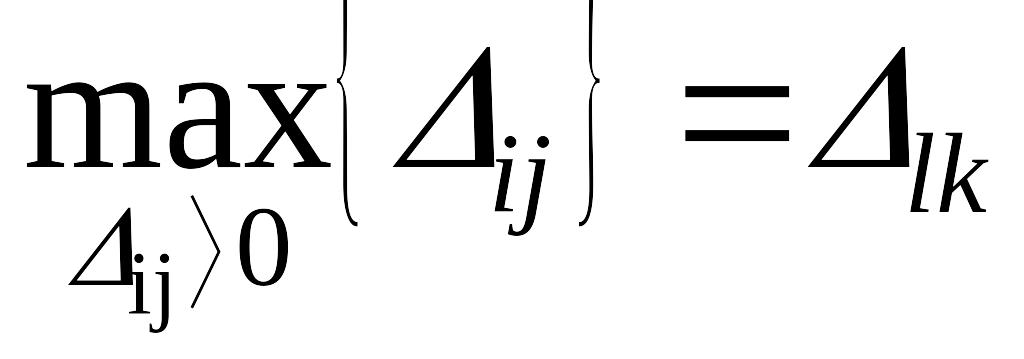
5. Переходят к новому опорному решению, на котором значение целевой функции будет меньше. Для этого находят клетку таблицы задачи, которой соответствует наибольшая положительная оценка . Строят цикл, включающий в свой состав данную клетку и часть клеток, занятых опорным решением. В клетках цикла расставляют поочередно знаки «+» и «-», начиная с «+» в клетке с наибольшей положительной оценкой. Осуществляют сдвиг (перераспределение груза) по циклу на величину θ= . Клетка со знаком «-», в которой достигается , остается пустой. Если минимум достигается в нескольких клетках, то одна из них остается пустой, а в остальных проставляют базисные нули, чтобы число занятых клеток оставалось равным т+ п—1. Возвращаются к пункту 3.
Пример. Решить транспортную задачу, данные приведены в таблице