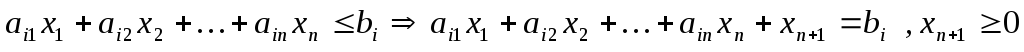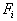Типичные задачи линейного программирования

6. Постановка задач линейного программирования. Примеры, различные формы задач и подходы решения. Постановка задач линейного программирования

Линейное программирование — область математики, разрабатывающая теорию и численные методы решения задач нахождения экстремума (максимума или минимума) линейной функции многих переменных при наличии линейных ограничений, т. е. равенств или неравенств, связывающих эти переменные.

В общей постановке задача линейного программирования (ЗЛП) формулируется следующим образом. Имеются какие-то переменные x = (x1, x2,…, xn) и линейная функция этих переменных, которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции при условии, что переменные x удовлетворяют системе линейных равенств и/или неравенств.

Функция цели в задаче линейного программирования обычно записывается так:

Или в сокращённом виде с сигмой:

Можно встретить обозначение целевой функции и через C, и через F.

Система ограничений в задаче линейного программирования в канонической форме записывается так:

И система ограничений, и целевая функция имеют линейный характер, то есть содержат переменные только в первой степени.

Целевая функция. Её нужно максимизировать или минимизировать. Для того, чтобы функцию максимизировать, переменные, являющиеся её слагаемыми, должны принимать как можно большие значения в соответствии с условиями задачи. При минимизации — наоборот, меньшие. Обычно целевая функция выражает доходы или расходы.

Переменные. Каждая переменная, как правило, означает запасы одного из производственных факторов — вида сырья, времени, рабочей силы, технологических возможностей или чего-либо другого.

Ограничения. Очень просто. Например, в каждом уравнении (неравенстве) заданы ограничения перечисленных выше или других запасов, используемых для производства определённого вида продукции.

Примеры, различные формы задач и подходы решения

Задача линейного программирования математически может быть представлена в различных формах.

Общей задачей ЛП называется задача, которая состоит в определении максимального (минимального) значения функции

Помимо общей формы, различают еще две частные задачи линейного программирования — стандартную и основную.

Особенностью стандартной задачи ЛП является то, что ее ограничения представлены в виде линейных неравенств, а также условий неотрицательности на переменные, присутствующие в задаче:

Ограничения основной задачи ЛП представляют собой линейные ограничения-равенства, а также условия неотрицательности на переменные:

Задачи линейного программирования в случае двух переменных можно решить и графическим методом, в случаях, когда переменных больше, применяется симплекс-метод.

Примеры решения задач линейного программирования:

Пример №1. Предприятие выпускает продукцию двух разновидностей. Каждый вид продукции проходит обработку на трёх станках. При обработке 1 т продукции I вида первый станок используется 0 ч, второй станок – 1 ч, третий станок – 1 ч. При обработке 1 т продукции II вида первый станок используется 1 ч, второй станок – 4 ч, третий станок – 1 ч. Время работы станков ограничено и не может превышать для первого станка 7 ч, для второго 29 ч, для третьего 11 ч. При реализации 1 т продукции I вида предприятие получает прибыль 2 руб., а при реализации 1 т продукции II вида – 5 руб. Найти оптимальный план выпуска продукции каждого вида, дающий максимальную прибыль от реализации всей продукции.

3. Решим прямую задачу графически:

Источник

Основные формы и задачи лп

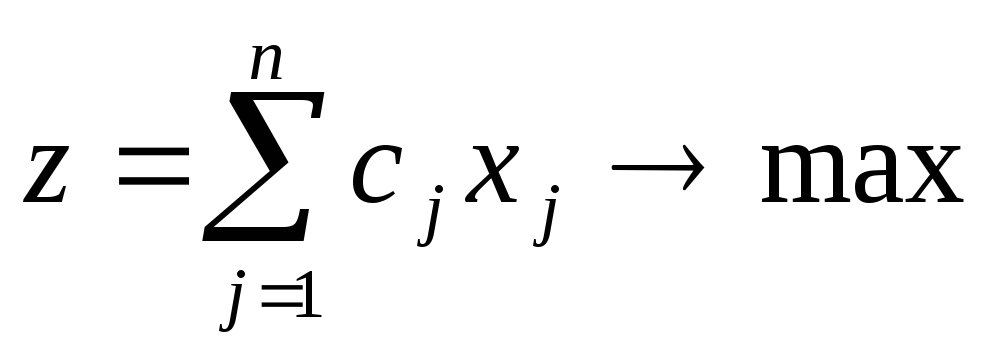
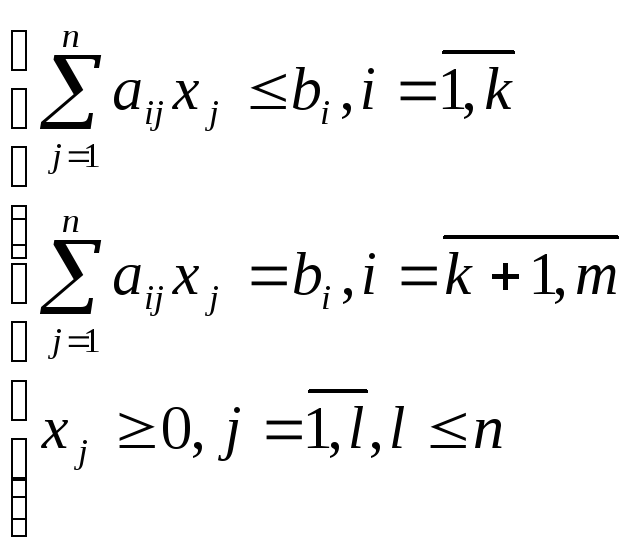
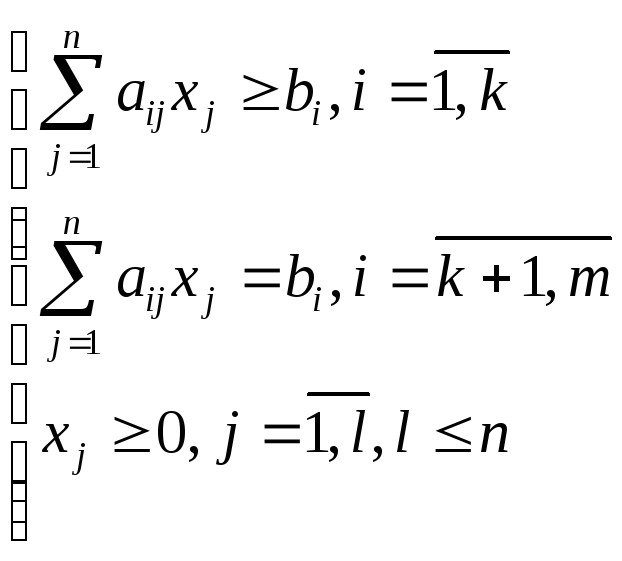
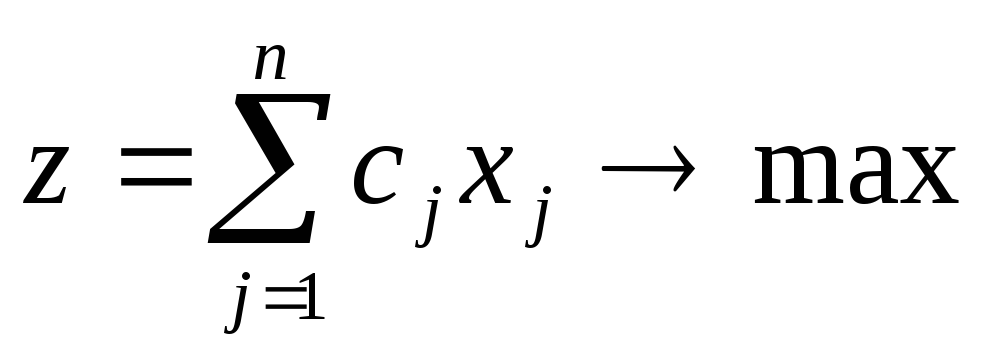
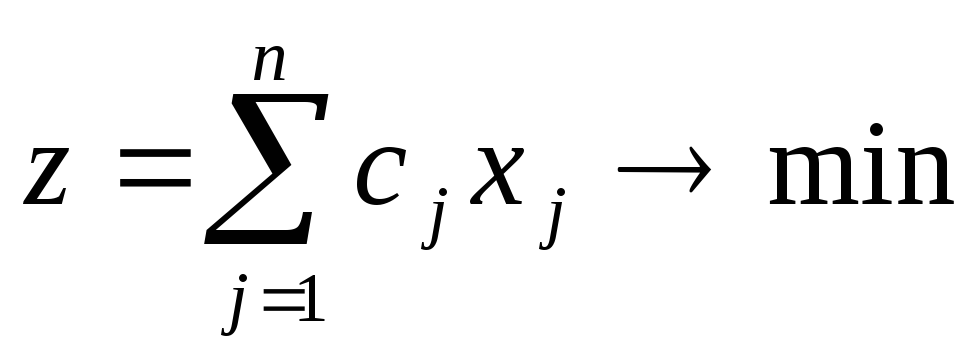
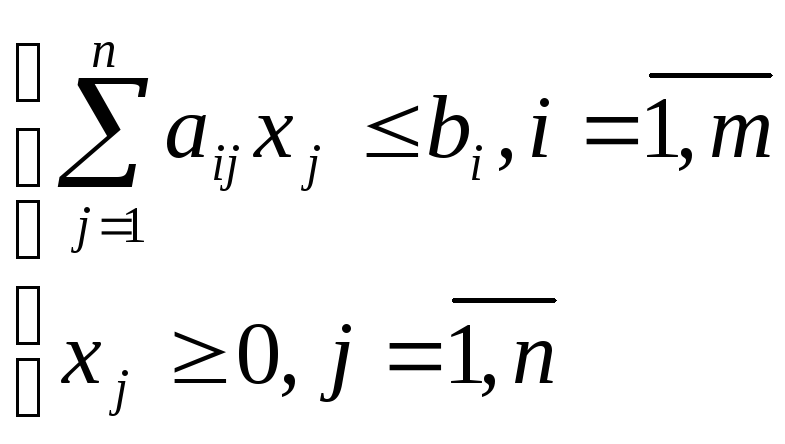
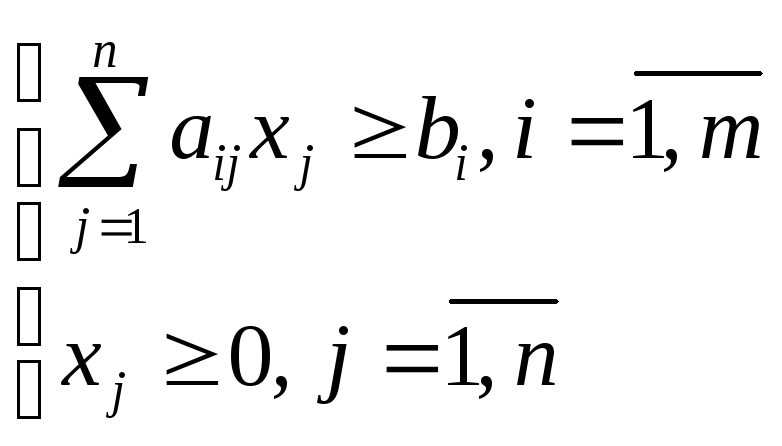
Общая задача ЛП (ОЗЛП): Целевая функция или Система ограничений или Стандартная (симметричная) задача ЛП: Целевая функция или Система ограничений (k=m, l=n) или Каноническая (основная) задача ЛП: Целевая функция Система ограничений (k=0,l=n) Стандартная форма – большое число прикладных моделей сводится к этой форме. Каноническая форма – основные варианты симплекс-метода разработаны для этой формы. Указанные три формы ОЗЛП эквивалентны – каждая из них может с помощью несложных преобразований может быть приведена к любой из них. Любую задачу ЛП можно привести к каноническому виду.

Способы перехода к каноническому виду

1)Сведение задач минимизации к задачам максимизации: 2)Переход от ограничений-неравенств к ограничениям-равенствам. 3)Замена отрицательных переменных неотрицательными

Типовые задачи линейного программирования

Задача о планировании производства

Предприятие производит изделия трех видов U₁,U₂,U₃. По каждому виду изделия предприятию спущен план, по которому оно обязано выпустить не менее b₁ единиц изделия U₁, не менее b₂ единиц изделия U₂ и не менее b₃ единиц изделия U₃. План может быть перевыполнен, но в определенных границах; условия спроса ограничивают количества произведенных единиц каждого типа: β₁, β₂, β₃ единиц. На изготовление изделий идет какое-то сырье; всего имеется четыре вида сырья s₁,s₂,s₃,,s₄ , причем запасы ограничены числами γ₁, γ₂, γ₃, γ₃ единиц каждого вида сырья. Теперь надо указать, какое количество сырья каждого вида идет на изготовление каждого вида изделий. Обозначим a_ij количество единиц сырья вида s₁ (i = 1, 2, 3, 4), потребное на изготовление одной единицы изделия U_j (j = 1, 2, 3). Первый индекс у числа a_ij – вид изделия, второй – вид сырья. Значения a_ij сведены в таблицу (матрицу).

Сырье	Изделия
	U1	U2	U3
s1	a11	a21	a31
s2	a12	a22	a32
s3	a13	a23	a33
s4	a14	a24	a34

При реализации единица изделия U₁ приносит предприятию прибыль с₁, U₂ – прибыль с₂, U₃ – прибыль с₃. Требуется так спланировать производство (сколько и каких изделий производить), чтобы план был выполнен или перевыполнен (но при отсутствии «затоваривания»), а суммарная прибыль обращалась бы в максимум. Запишем задачу в форме задачи линейного программирования. Элементами решения будут х₁, х₂, х₃ – количества единиц изделий U₁,U₂,U₃, которые мы произведем. 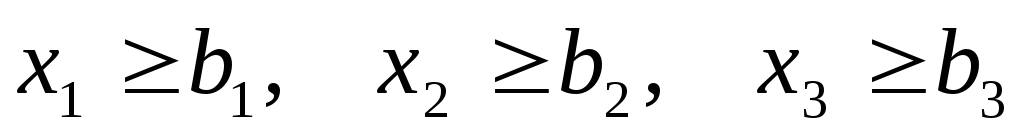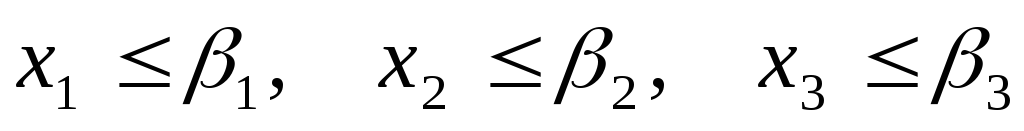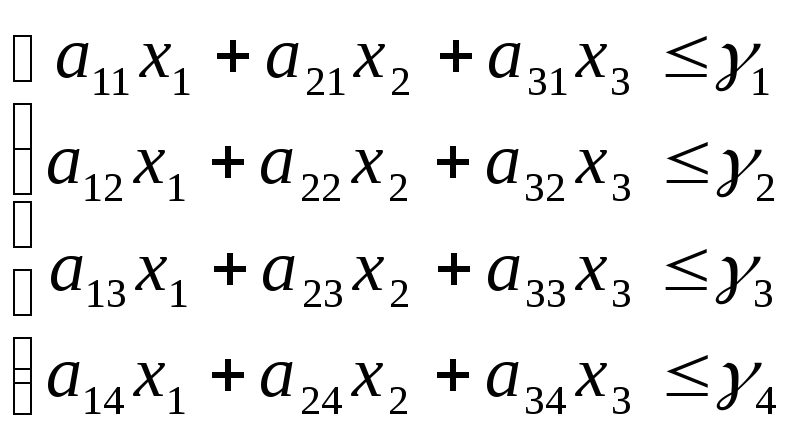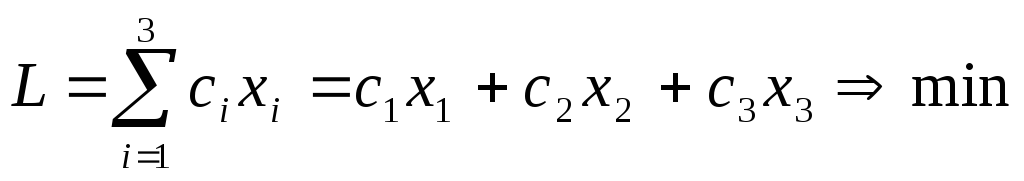Обязательность выполнения планового задания запишется в виде трех ограничений-неравенств: Отсутствие излишней продукции (затоваривания) даст нам еще три ограничения-неравенства: Кроме того, нам должно хватить сырья. Соответственно четырем видам сырья будем иметь четыре ограничения-неравенства: Прибыль, приносимая планом (х₁, х₂, х₃), будет равна L= с₁х₁+ с₂х₂+ с₃х₃. Таким образом, мы снова получили задачу линейного программирования: найти такие неотрицательные значения переменных х₁, х₂, х₃,, чтобы они удовлетворяли ограничениям – неравенствам и одновременно обращали в максимум линейную функцию этих переменных:. В более общем виде задача формулируется следующим образом. Пусть некоторое предприятие производит n типов товаров, затрачивая при этом m типов ресурсов. Известны следующие параметры:

• a_ij – количество i—го ресурса, необходимое для производства единичного количества j-го товара, a_ij≥0 (i= 1,…,m,j= 1,…,n);
• b_i – запас i—го ресурса на предприятии, b_i≥0;
• с_j– цена единичного количества j-го товара, с_j≥0.

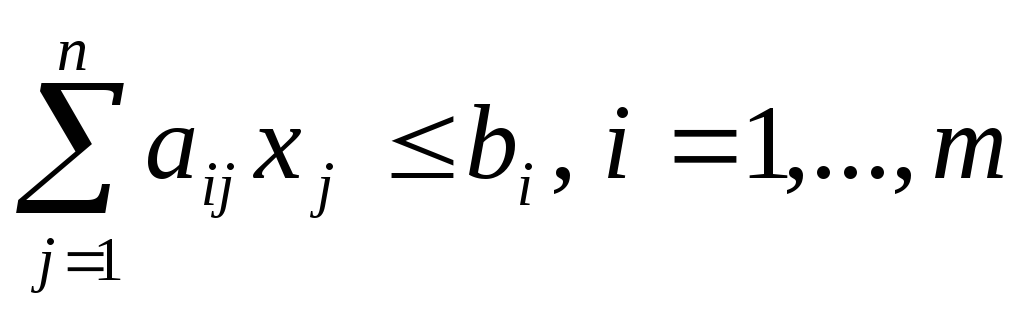
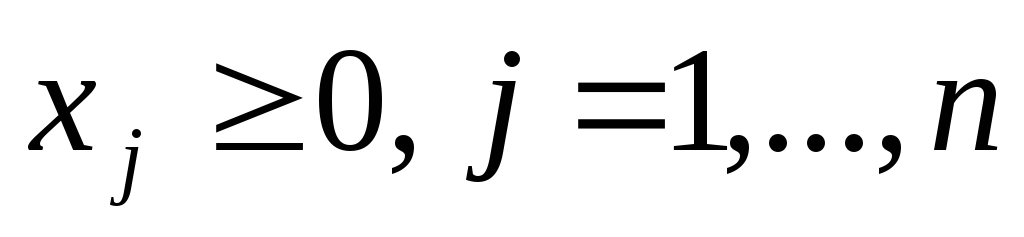
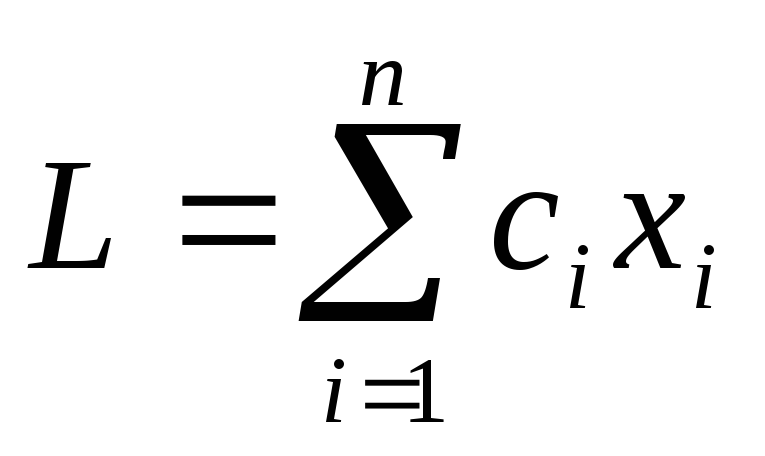
Предполагается, что технология производства линейна, то есть затраты ресурсов растут прямо пропорционально объему производства. Пусть число х_j показывает планируемый объем производства j-го товара. Тогда допустимым является только такой набор производимых товаров х=(х₁, …, х_n), при котором суммарные затраты каждого i—го ресурса не превосходят его запаса: . (I) Кроме того, имеем следующие естественные ограничения: . (II) Стоимость набора товаров х выражается величиной (III) Задача планирования производства ставится следующим образом: среди всех векторов х, удовлетворяющих условиям (I), (II), найти такой, при котором величина (III) принимает наибольшее значение.

Источник

Линейное программирование

1.1. Примеры моделей, приводящих к задачам линейного программирования

Линейное программирование является одной из основных частей того раздела современной математики, который получил название математического программирования. В общей постановке задачи этого раздела выглядят следующим образом.

Имеются какие-то переменные и функция этих переменных , которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции при условии, что переменные x принадлежат некоторой области G:

В зависимости от вида функции и области G и различают разделы математического программирования: квадратичное программирование, выпуклое программирование, целочисленное программирование и т.д. Подробнее об этом будет сказано в заключении.

Линейное программирование характеризуется тем, что

является линейной функцией переменных ;

б) область G определяется системой линейных равенств или неравенств.

Чтобы понять, откуда берутся задачи линейного программирования, рассмотрим некоторые, уже ставшие классическими, примеры подобных задач.

Задача о диете

Задача о диете возникает при составлении наиболее экономного (т.е. наиболее дешевого) рациона питания животных, удовлетворяющего определенным медицинским требованиям.

Предположим, что в нашем распоряжении имеется n продуктов питания (сено, зерно, комбикорм, соль и т.д.). Обозначим эти продукты через

. Предположим, что

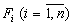
есть стоимость единицы веса (например,

стоимость одного килограмма) продукта .

Рациональная диета должна доставлять животному определенные компоненты (белки, жиры, углеводы, витамины, микроэлементы и т.д.). Обозначим эти компоненты через . Тогда можно составить таблицу — справочник, указывающую, какое количество каждого компонента имеется в единице веса каждого продукта.

Источник