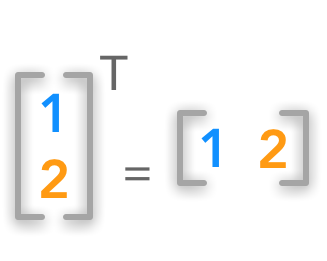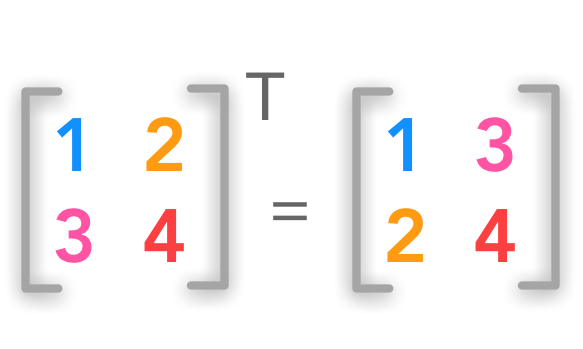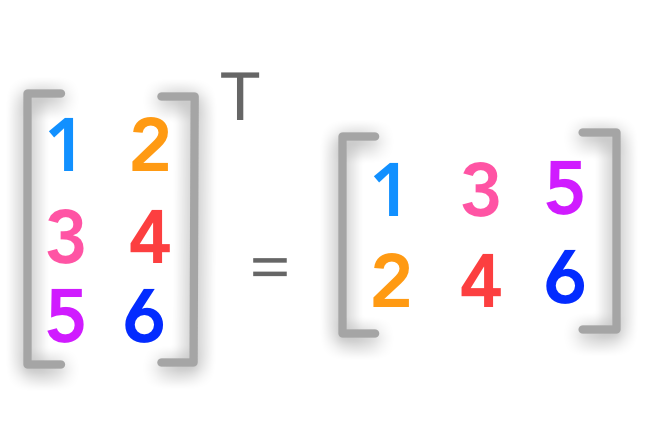Square a matrix python

Python how to square a matrix in python

Solution 1: Using list comprehension: Solution 2: List comprehensions can be nested: In this case would be your matrix Solution 3: Use numpy: A list comprehension could look like this To raise a square matrix to the power n in Linear Algebra, use the numpy.linalg.matrix_power() in Python For positive integers n, the power is computed by repeated matrix squarings and matrix multiplications. For positive integers n, the power is computed by repeated matrix squarings and matrix multiplications.

Python function for creating a square matrix of any size

is it OK to just use NumPy?

import numpy as np def square_matrix(size, *elements): return np.array(elements).reshape(size, size) 

For the matrix creation, you could use list comprehension which is more efficient than a for a loop.

You could replace the for loops in the else part of your if statement by the below code.

matrix = [[i for i in elements[j:j+size]] for j in range(0,len(elements),size)] 

There is no need to give the size as an argument. If the square root of the length of the arguments is a whole number, then you can make a square matrix of the elements.

import numpy as np from math import sqrt def square_matrix(*elements): size = sqrt(len(elements)) if size.is_integer(): return np.array(elements).reshape(int(size), int(size)) else: raise RuntimeError("Number of elements is not sufficient to make a square matrix") print(square_matrix(1, 2, 3, 4, 5, 6, 7, 8, 9)) # Output: # array([[1, 2, 3], # [4, 5, 6], # [7, 8, 9]]) 

Python matrix manipulation, where all the elements in the list become squared? I’m trying to do list comprehension. python list matrix list-comprehension · Share.

Square matrix in python 😀

Python matrix manipulation

>>> lis = [[2,0,2],[0,2,0],[2,0,2]] >>> [[y**2 for y in x] for x in lis] [[4, 0, 4], [0, 4, 0], [4, 0, 4]] 

List comprehensions can be nested:

sqd = [[elem*elem for elem in inner] for inner in outer] 

In this case outer would be your matrix matrix

>>>> matrix = [[2,0,2],[0,2,0],[2,0,2]] >>>> sqd = [[elem*elem for elem in inner] for inner in matrix] >>>> sqd [[4, 0, 4], [0, 4, 0], [4, 0, 4]] 

import numpy as np matrix = [[2,0,2],[0,2,0],[2,0,2]] np_matrix = np.array(matrix) np_matrix**2 

A list comprehension could look like this

matrix2 = [ [e*e for e in l] for l in matrix ] 

Raise a square matrix to the power n in Linear Algebra using, Raise a square matrix to the power n in Linear Algebra using NumPy in Python In this article, we will discuss how to raise a square matrix to

Raise a square matrix to the power n in Linear Algebra in Python

To raise a square matrix to the power n in Linear Algebra, use the numpy.linalg.matrix_power() in Python For positive integers n, the power is computed by repeated matrix squarings and matrix multiplications. If n == 0, the identity matrix of the same shape as M is returned. If n < 0, the inverse is computed and then raised to the abs(n).

The return value is the same shape and type as M; if the exponent is positive or zero then the type of the elements is the same as those of M. If the exponent is negative the elements are floating-point. The 1st parameter, a is a matrix to be “powered”. The 2nd parameter, n is the exponent that can be any integer or long integer, positive, negative, or zero.

Steps

At first, import the required libraries −

import numpy as np from numpy.linalg import matrix_power

Create a 2D array, matrix equivalent of the imaginary unit −

print("\nDimensions of our Array. \n",arr.ndim)

print("\nDatatype of our Array object. \n",arr.dtype)

print("\nShape of our Array object. \n",arr.shape)

To raise a square matrix to the power n in Linear Algebra, use the numpy.linalg.matrix_power() in Python. For positive integers n, the power is computed by repeated matrix squarings and matrix multiplications. If n == 0, the identity matrix of the same shape as M is returned. If n < 0, the inverse is computed and then raised to the abs(n) −

print("\nResult. \n",matrix_power(arr, 0))

Example

import numpy as np from numpy.linalg import matrix_power # Create a 2D array, matrix equivalent of the imaginary unit arr = np.array([[0, 1], [-1, 0]]) # Display the array print("Our Array. \n",arr) # Check the Dimensions print("\nDimensions of our Array. \n",arr.ndim) # Get the Datatype print("\nDatatype of our Array object. \n",arr.dtype) # Get the Shape print("\nShape of our Array object. \n",arr.shape) # To raise a square matrix to the power n in Linear Algebra, use the numpy.linalg.matrix_power() in Python print("\nResult. \n",matrix_power(arr, 0))

Output

Our Array. [[ 0 1] [-1 0]] Dimensions of our Array. 2 Datatype of our Array object. int64 Shape of our Array object. (2, 2) Result. [[1 0] [0 1]]

Python program to multiply two matrices, Time Complexity: O(M*M*N), as we are using nested loop traversing, M*M*N. Auxiliary Space: O(M*N), as we are using a result matrix which is

Split matrix in python into square matrices?

You may do this in one line (using numpy) by:

test = np.arange(35).reshape(5,7) M, N = test.shape A = 2 print(test) print('\n') split_test = test[0:M-M%A, 0:N-N%A].reshape(M//A, A, -1, A).swapaxes(1, 2).reshape(-1, A, A) print(split_test) 

[[ 0 1 2 3 4 5 6] [ 7 8 9 10 11 12 13] [14 15 16 17 18 19 20] [21 22 23 24 25 26 27] [28 29 30 31 32 33 34]] [[[ 0 1] [ 7 8]] [[ 2 3] [ 9 10]] [[ 4 5] [11 12]] [[14 15] [21 22]] [[16 17] [23 24]] [[18 19] [25 26]]] 

If you are ok with using skimage:

a = np.r_[np.add.outer((1,6,1,6),range(4)),[[0,0,0,0]]] from skimage.util import view_as_windows sz = 2,2 view_as_windows(a,sz,sz) # array([[[[1, 2], # [6, 7]], # # [[3, 4], # [8, 9]]], # # # [[[1, 2], # [6, 7]], # # [[3, 4], # [8, 9]]]]) 

Python — Multiplying many square matrices, I don’t know a fully vectorized solution. Initially I thought that np.matmul.reduce might work, but reduce seems to be unsupported for

Источник

How to square a matrix in Numpy?

Following is a tutorial on how to square a matrix in Numpy Python library.

Using a numpy square method

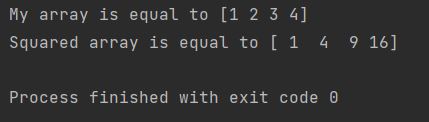
The easiest way and the most convenient one is just to use a built-in function of Numpy square. It just take my array as an argument and squares it.

import numpy as np my_array = np.array([1, 2, 3, 4]) squared_array = np.square(my_array) print(f"My array is equal to ") print(f"Squared array is equal to ")

As an output you can see that my array got squared as expected.

Using a numpy power method

You can also use power Numpy method. Square is the same as second power so it will work the same.

import numpy as np my_array = np.array([1, 2, 3, 4]) squared_array = np.power(my_array, 2) print(f"My array is equal to ") print(f"Squared array is equal to ")

Using asterisks

The most pythonic way would be to use ** 2 which also square my array.

import numpy as np my_array = np.array([1, 2, 3, 4]) squared_array = my_array ** 2 print(f"My array is equal to ") print(f"Squared array is equal to ")

These are 3 different ways to square a matrix using Numpy. Of course Numpy square function is the most efficient one for a comercial purpose.

Categories

RSS

Tags

We use cookies on our website to give you the most relevant experience by remembering your preferences and repeat visits. By clicking “Accept”, you consent to the use of ALL the cookies.

Privacy Overview

This website uses cookies to improve your experience while you navigate through the website. Out of these, the cookies that are categorized as necessary are stored on your browser as they are essential for the working of basic functionalities of the website. We also use third-party cookies that help us analyze and understand how you use this website. These cookies will be stored in your browser only with your consent. You also have the option to opt-out of these cookies. But opting out of some of these cookies may affect your browsing experience.

Necessary cookies are absolutely essential for the website to function properly. This category only includes cookies that ensures basic functionalities and security features of the website. These cookies do not store any personal information.

Any cookies that may not be particularly necessary for the website to function and is used specifically to collect user personal data via analytics, ads, other embedded contents are termed as non-necessary cookies. It is mandatory to procure user consent prior to running these cookies on your website.

Источник

Introduction

This is the first post/notebook of a series following the syllabus of the linear algebra chapter from the Deep Learning Book by Goodfellow et al.. This work is a collection of thoughts/details/developements/examples I made while reading this chapter. It is designed to help you go through their introduction to linear algebra. For more details about this series and the syllabus, please see the introduction post.

This first chapter is quite light and concerns the basic elements used in linear algebra and their definitions. It also introduces important functions in Python/Numpy that we will use all along this series. It will explain how to create and use vectors and matrices through examples.

2.1 Scalars, Vectors, Matrices and Tensors

Let’s start with some basic definitions:

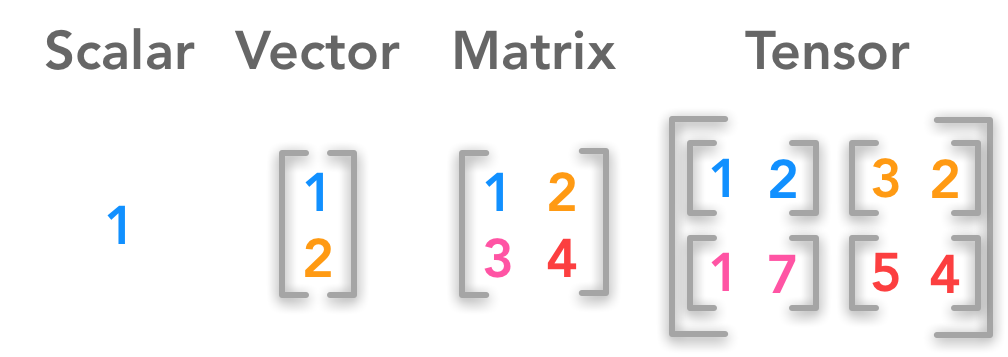
Difference between a scalar, a vector, a matrix and a tensor

• A scalar is a single number
• A vector is an array of numbers.

$ \bs =\begin x_1 \\ x_2 \\ \cdots \\ x_n \end $

• scalars are written in lowercase and italics. For instance: $n$
• vectors are written in lowercase, italics and bold type. For instance: $\bs$
• matrices are written in uppercase, italics and bold. For instance: $\bs$

Example 1.

Create a vector with Python and Numpy

Coding tip: Unlike the matrix() function which necessarily creates $2$-dimensional matrices, you can create $n$-dimensionnal arrays with the array() function. The main advantage to use matrix() is the useful methods (conjugate transpose, inverse, matrix operations…). We will use the array() function in this series.

We will start by creating a vector. This is just a $1$-dimensional array:

Example 2.

Create a (3×2) matrix with nested brackets

The array() function can also create $2$-dimensional arrays with nested brackets:

Shape

The shape of an array (that is to say its dimensions) tells you the number of values for each dimension. For a $2$-dimensional array it will give you the number of rows and the number of columns. Let’s find the shape of our preceding $2$-dimensional array A . Since A is a Numpy array (it was created with the array() function) you can access its shape with:

Let’s check the shape of our first vector:

As expected, you can see that $\bs$ has only one dimension. The number corresponds to the length of the array:

Transposition

With transposition you can convert a row vector to a column vector and vice versa:

Vector transposition

Square matrix transposition

If the matrix is not square the idea is the same:

Non-square matrix transposition

The superscript $^\text$ is used for transposed matrices.

The shape ($m \times n$) is inverted and becomes ($n \times m$).

Dimensions of matrix transposition

Example 3.

Create a matrix A and transpose it

We can check the dimensions of the matrices:

We can see that the number of columns becomes the number of rows with transposition and vice versa.

Addition

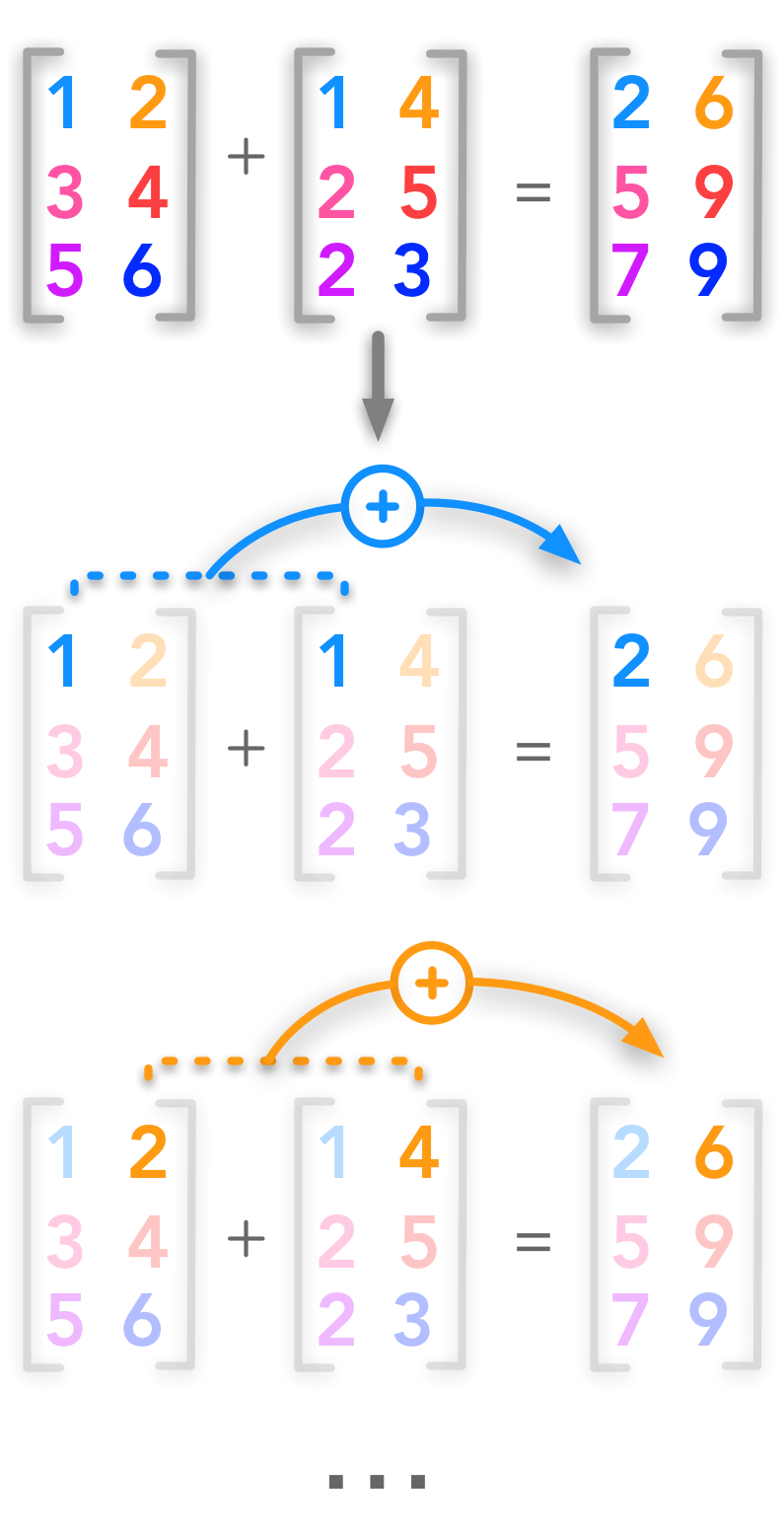
Addition of two matrices

Matrices can be added if they have the same shape:

$i$ is the row index and $j$ the column index.

Example 4.

Create two matrices A and B and add them

With Numpy you can add matrices just as you would add vectors or scalars.

# Add matrices A and B C = A + B C 

It is also possible to add a scalar to a matrix. This means adding this scalar to each cell of the matrix.

$ \alpha+ \begin A_ & A_ \\ A_ & A_ \\ A_ & A_ \end= \begin \alpha + A_ & \alpha + A_ \\ \alpha + A_ & \alpha + A_ \\ \alpha + A_ & \alpha + A_ \end $

Example 5.

Add a scalar to a matrix

# Exemple: Add 4 to the matrix A C = A+4 C 

Broadcasting

Numpy can handle operations on arrays of different shapes. The smaller array will be extended to match the shape of the bigger one. The advantage is that this is done in C under the hood (like any vectorized operations in Numpy). Actually, we used broadcasting in the example 5. The scalar was converted in an array of same shape as $\bs$.

Here is another generic example:

where the ($3 \times 1$) matrix is converted to the right shape ($3 \times 2$) by copying the first column. Numpy will do that automatically if the shapes can match.

Example 6.

Add two matrices of different shapes

You can find basics operations on matrices simply explained here.

References

Feel free to drop me an email or a comment. The syllabus of this series can be found in the introduction post. All the notebooks can be found on Github.

Источник