Создание компилятора на python

JIT-компилятор Python в 300 строк

Может ли студент второго курса написать JIT-компилятор Питона, конкурирующий по производительности с промышленным решением? С учётом того, что он это сделает за две недели за зачёт по программированию.

Как оказалось, может, но с нюансами.

Предисловие

Обучаясь в РТУ МИРЭА, на специальности «Программная инженерия» я попал на семестровый курс программирования на Питоне. Питон я знал до этого, поэтому не хотелось много с ним возиться. Благо творчество студентов поощряется, иногда даже «автоматами». Собственно, стимулируемый этим «автоматом» и тягой к написанию системных модулей я написал JIT-компилятор, который назвал MetaStruct.

С кодом проекта можно ознакомиться в репозитории.

Предыдущий мой опыт в написании низкоуровневых программ оказался нежизнеспособным и весьма поучительным. Но об этом сегодня речь не пойдёт.

Стандартная реализация Python — CPython — достаточно медленная. В сравнении с C++ называют замедление в 20-30 раз. Но целое сообщество программистов на Питоне готовы заплатить эту цену ради удобства синтаксиса, быстроты написания, изящности и выразительности кода.

На этой почве появляются разнообразные способы оптимизации выполнения программ на Питоне. Такие диалекты как Cython и RPython пытаются решить проблему «разгона» Питона за счёт статической типизации и компиляции модулей.

В области JIT-компиляции промышленным решением является проект Numba, спонсируемый такими технологическими гигантами как Intel, AMD и NVIDIA. Именно с этим пакетом мне предложили и посоревноваться, написав миниатюрный JIT-компилятор программ на Питоне.

В этой статье я хочу рассказать, с какими трудностями я, как программист достаточно прикладной, столкнулся при написании такой довольно низкоуровневой вещи, как миниатюрный JIT-компилятор.

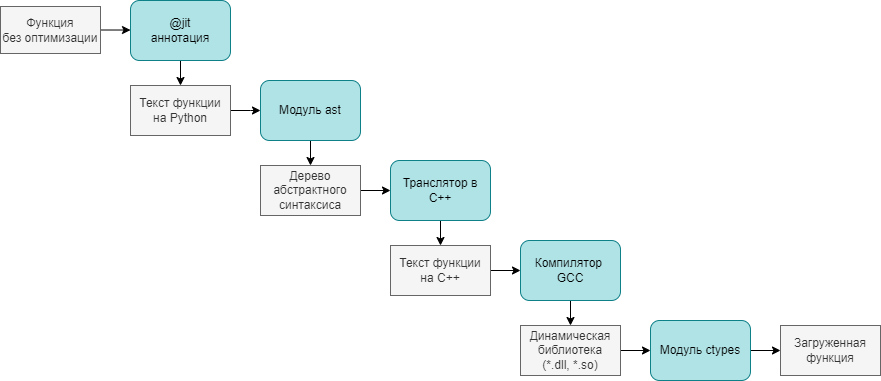
Принцип работы

На схеме выше показано, какие этапы проходит функция на Питоне, становясь скомпилированным модулем на С++:

@jit def sum(x: int, y: int) -> int: res: int = x + y return res

1. Аннотация, получая объект функции, с помощью inspect.getsource(func_object) получает текст функции в виде строки.
2. С помощью функции ast.parse(func_py_text) текст функции превращается в абстрактное синтаксическое дерево (AST) языка Питон
3. Моя программа проходится по дереву через метод visit() , наследуясь от ast.NodeVisitor , и получает на выходе текст программы на C++, который записывается в файл. Для примера выше, он будет примерно таким:

extern "C" int sum(int x, int y)

1. Через subprocess.run() происходит вызов компилятора g++, который выдаёт динамически подключаемую библиотеку (в зависимости от платформы файлом .dll или .so )

g++ -O2 -c source.cpp -o object.o g++ -shared object.o -o lib.dll

1. При помощи вызова ctypes.LibraryLoader(CDLL).LoadLibrary(dll_filename) Динамическая библиотека подключается к среде выполнения и даёт доступ к скомпилированному варианту исходной функции.
2. Конечный пользователь, добавивший над функцией аннотацию @jit , пользуется совершенно другим вариантом своего кода, ничего не подозревая.

Процесс достаточно трудоёмкий для функции сложения из примера, но при частых вызовах и большом количестве вычислений внутри функции время компиляции окупается.

Если бы это был не Питон, а какой-нибудь предметно-ориентированный язык, то пришлось бы писать парсер и обход получившегося абстрактного дерева, и решение не было бы уже таким коротким. Но в моём случае, инфраструктура Питона и его гибкость сыграли мне на руку.

Впечатляющие результаты

Наверное, стоит от технической части переходить к части визуализации и маркетинга.

Созданный алгоритм JIT-компиляции был протестирован на нескольких простых алгоритмических задачах:

• Сумма двух чисел.
• Хеш-функция для целых чисел.
• Вычисление экспоненты через ряд Тейлора.
• Числа Фибоначчи.

С расчётами и графиками можно подробнее ознакомиться в
Jupyter-блокноте

Для оценки времени выполнения использованы функции timeit() и repeat() модуля timeit . Для отрисовки графиков — модуль matplotlib

В примерах будут сравниваться четыре реализации функций:

• Просто функции питона.
• Оптимизированные аннотацией @jit .
• Оптимизированные аннотацией @numba.jit .
• Запущенные на интерпретаторе PyPy

Примечание: Я добавил к рассмотрению PyPy по просьбе одного из читателей. И этот метод оптимизации Питона действительно иногда является очень эффективным, что подтверждают графики ниже. Но при его использовании есть много нюансов.

Первый, это совершенно другая среда запуска, количество поддерживаемых библиотек которой значительно меньше, встроить в большой проект с уймой сторонних модулей просто так не получится.

Второй, версии PyPy выходят позже версий самого Питона. На момент написания статьи в PyPy не было конструкции match/case, поэтому пришлось использовать более простую и длинную реализацию обхода дерева.

Поэтому я призываю не сильно разочаровываться в jit-компиляторах, которые в отличие от PyPy не зависят от конкретной версии Питона и списка библиотек вашего проекта.

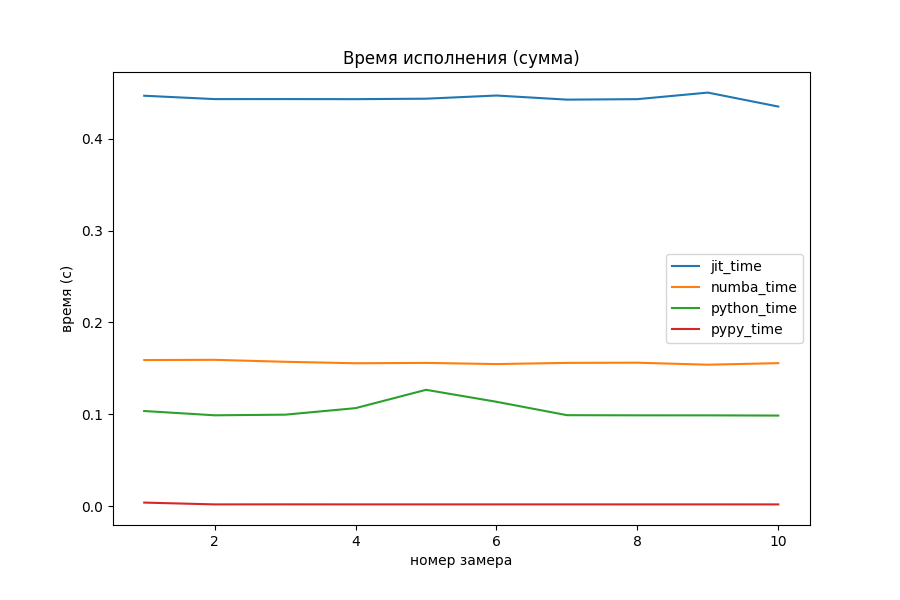
Сумма двух чисел

def py_sum(x: int, y: int) -> int: res: int = x + y return res

На задаче сложения двух целых чисел никакой оптимизации не видно, даже наоборот. Накладные расходы на вызов функции из dll-файла и обработка результата занимает много времени по сравнению с самими расчётами. Numba обставила моего «питомца» в 3 раза на этом примере.

Модуль PyPy отработал в 30 раз (0.003 секунды против 0.1 секунды) быстрее, чем CPython.

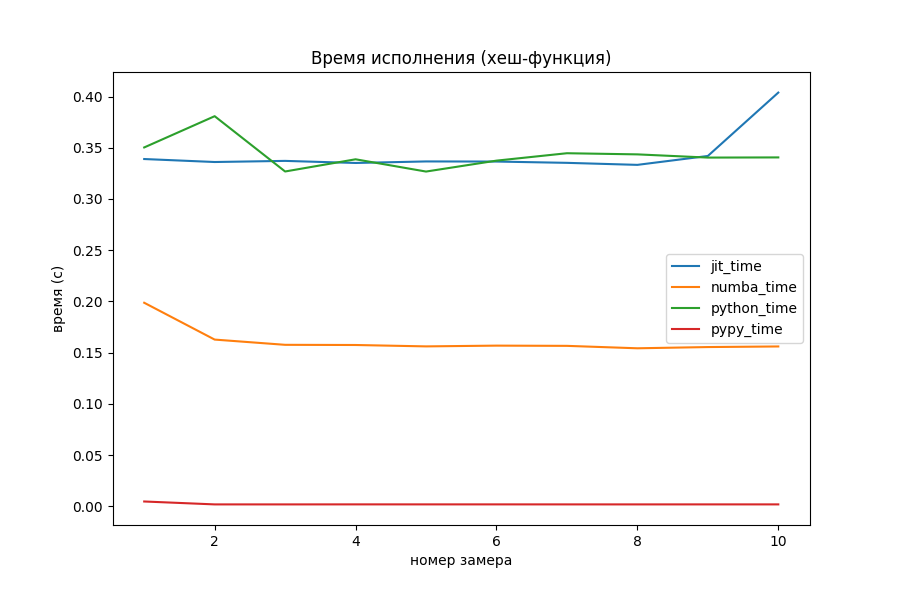
Хеш-функция для целых чисел

Обычно, для чисел из небольшого диапазона в качестве хеша используют их самих. Однако на просторах Интернета я нашёл такую хеш-функцию:

def py_hash(x: int) -> int: x = ((x >> 16) ^ x) * 0x45d9f3b x = ((x >> 16) ^ x) * 0x45d9f3b x = (x >> 16) ^ x return x

Автором сообщения утверждается, что значение параметра 0x45d9f3b позволяет достичь наибольшей «случайности» бит внутри числа. По крайней мере, для хеш-функций такого вида.

Numba оказалась хорошо оптимизированной под битовые операции. Не совсем понятно, откуда она взялась. Оставим этот вопрос открытым, но мне кажется, спонсорство главных производителей процессоров и видеокарт не прошло даром. Мой же вариант оказался слегка быстрее простого Питона, и то не всегда.

PyPy и тут обставил оптимизаторы, выполнив прогоны за 0.002 секунды, то есть в 100 раз быстрее, чем Numba.

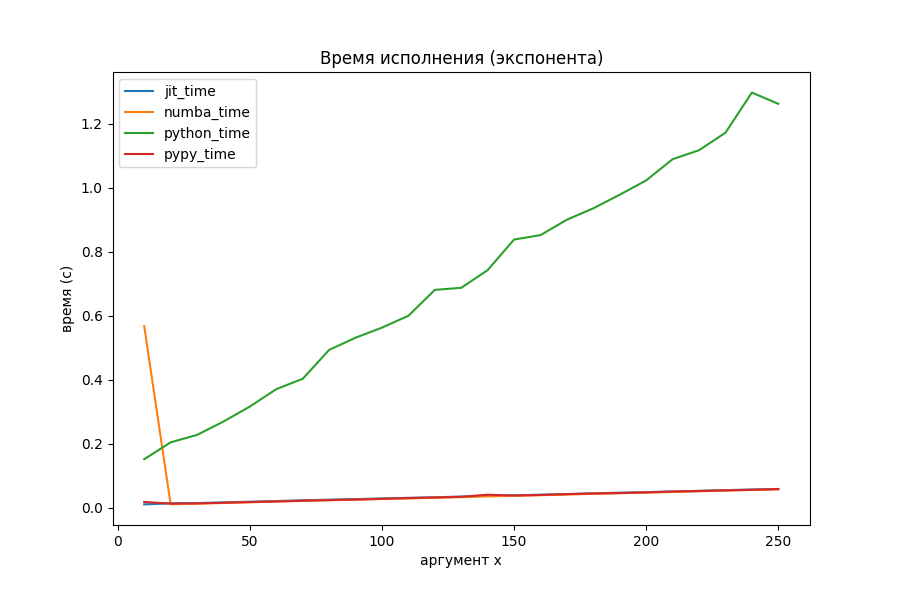
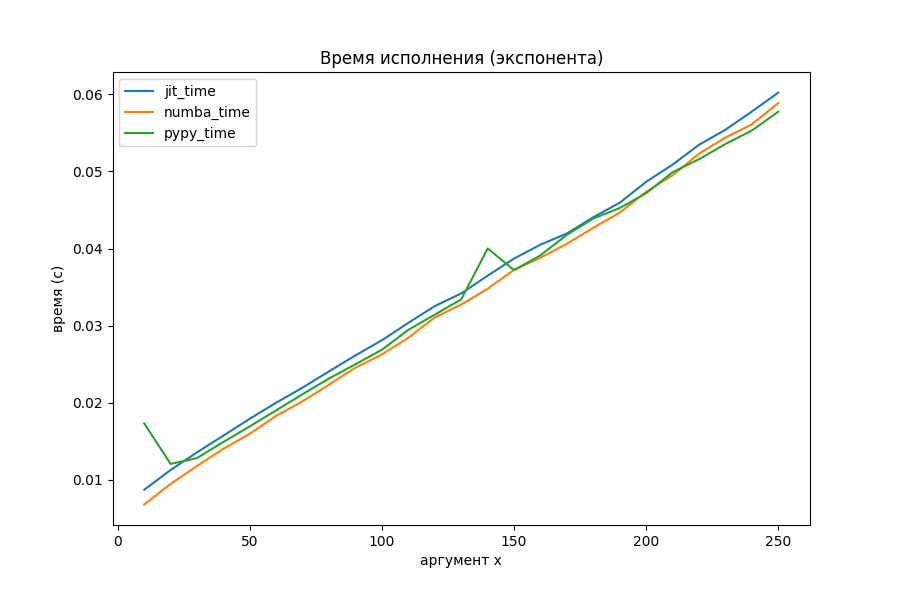
Вычисление экспоненты через ряд Тейлора

Странное большое время для маленького x, выяснилось, обосновано тем, что Numba делает какие-то отложенные шаги компиляции при первом запуске. На общей её производительности это почти никак не сказывается (на втором графике с методами оптимизации аномалия исчезла, потому что был произведён повторный прогон).

Питон явно показал себя неважно, поэтому посмотрим на двух оптимизаторов и PyPy отдельно.

def py_exp(x: float) -> float: res: float = 0 threshold: float = 1e-30 delta: float = 1 elements: int = 0 while delta > threshold: elements = elements + 1 delta = delta * x / elements while elements >= 0: res += delta delta = delta * elements / x elements -= 1 return res

Кому интересен матан, экспонента считается по формуле соответствующего ряда Тейлора:

Алгоритм прекращается, когда разница между дельтами двух итераций становится меньше порога, либо превращается в машинный ноль. Суммирование происходит от меньших членов к большим для уменьшения потерь точности.

Наконец-то моё творение начало соперничать с Numba. На больших объёмах вычислений однозначного лидера нет. PyPy уже потерял преимущество в два порядка и выполняется с такой же скоростью, как и jit-оптимизаторы.

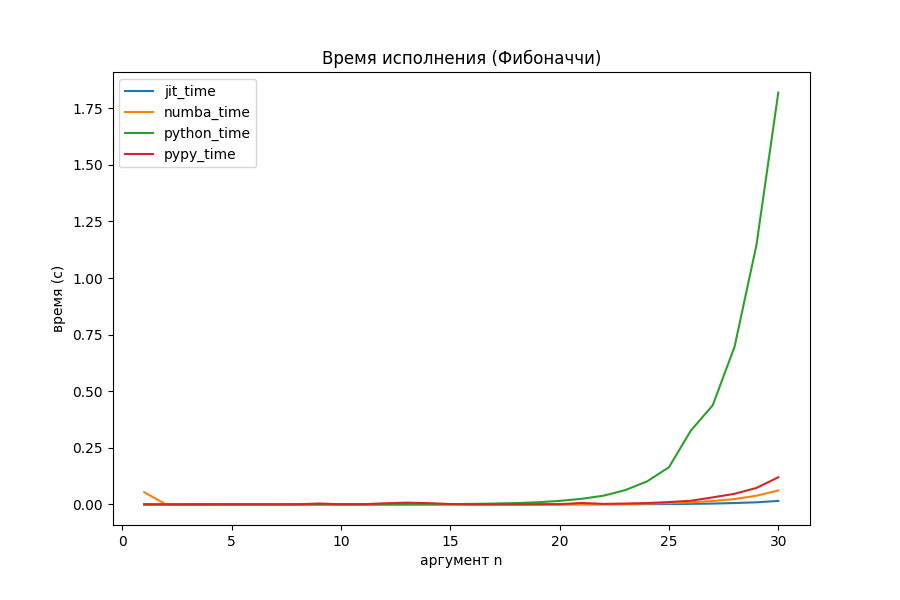
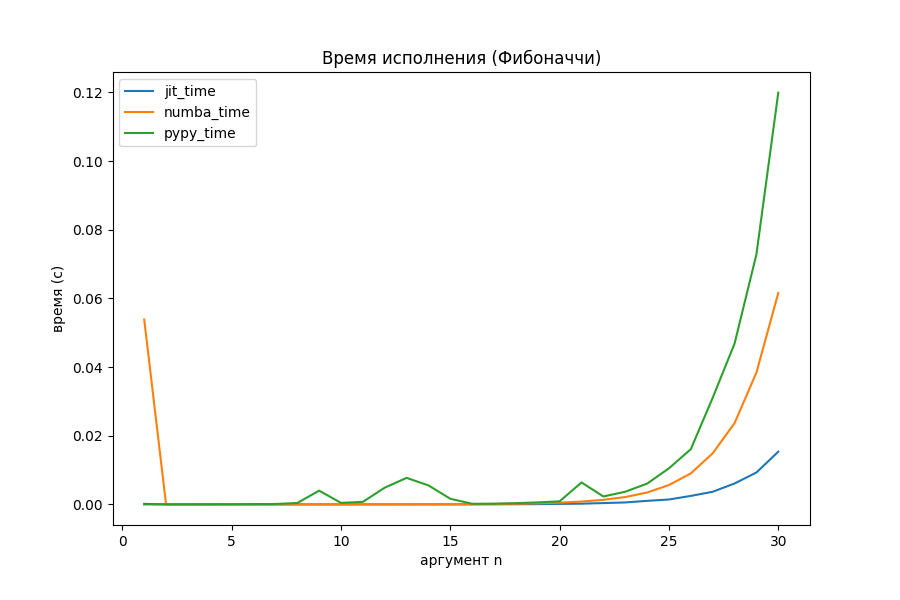
Числа Фибоначчи

Несмотря на то, что аннотация позволяет компилировать функции по одной, в ней всё ещё можно использовать рекурсию.

На рекурсии Питон вообще перестал за себя отвечать. Что там с оптимизаторами?

Внезапно, реализованная в проекте компиляция начала работать в 4 раза быстрее, чем Numba и в 8 раз быстрее PyPy. Получается, что с задачами разветвлённой рекурсии мой JIT-компилятор неплохо справляется.

Это одно из самых интересных мест всего исследования, которое можно было бы продолжить.

Мысли сходятся

На самом деле, такой подход к оптимизации не нов в мире программирования. Чем-то похожим занимался Владимир Макаров, оптимизируя Ruby до уровня языка передачи регистров RTL в своём проекте MJIT.

Существуют даже оптимизации сделанные поверх решения Макарова, о которых можно почитать здесь.

В частности, в исследованиях отмечается, что выбор компилятора, будь то GCC или LLVM, существенно не сказывается на производительности. В моём решении использован g++ из-за большей портируемости скомпилированного кода.

Для ускорения вычислений в проекте Ruby используются также предкомплированные заголовки. Однако, для студенческой работы такой уровень оптимизации не требуется.

Непредвиденные трудности

Конечно же, всё заработало не с первого раза. Вероятно, даже не с десятого. Поэтому хотелось бы привести здесь небольшую «работу над ошибками»

Типы данных

Питон медленный во многом из-за динамической типизации, так как довольно много времени уходит на определение типа переменной перед её использованием. Также, идеология «всё есть объект» раздувает примитивные типы данных до размера остальных объектов и классов. Чтобы ускорить вычисления, нужно использовать именно примитивы, а не объекты.

Проблема в том, что из кода на Питоне не всегда очевидно, какого типа будет переменная. Продвинутые оптимизаторы умеют определять тип переменной «на лету» из контекста. Я решил не усложнять жизнь , а усложнить код, и использовать аннотации типов.

Про использование аннотаций типов есть хорошие статьи в официальной документации или на Хабре.

Пусть нужно скомпилировать ту самую функцию сложения:

def sum(x, y): res = x + y return res

Какой-нибудь компилируемый язык, C++ например, за такую программу спасибо не скажет. Добавим аннотации:

def sum(x: int, y: int) -> int: res: int = x + y return res

В этом примере явного объявления типов требуют три вещи:

В базовой реализации будет только три типа данных:

Источник