Solving quadratic equation in java

Program to find Solution of Quadratic Equation in JAVA

This program finds the solutions of a Quadratic Equation by using Sri Dharacharya Formula in JAVA.

A Quadratic Equation is of the form ax2+bx+c=0 where x2 is x raised to the power 2.Here ,a,b,and c are the respective coefficients of the Quadratic expression.

Sri Dharacharya formula states that the roots of the Quadratic Expression will be x=(-b+Under root(b2-4ac))/2a and x=(-b-Under root(b2-4ac))/2a.

This formula has been used in the program to determine both the roots as per the value of the discriminants.

import java.util.*;
public class QuadraticSolution
public static void main(String args[])
Scanner ob=new Scanner(System.in);
System.out.println(«An quadratic expression is like ax^2+bx+c=0»);
System.out.println(«Enter the coefficient of x^2»);
double a=ob.nextDouble();
System.out.println(«Enter the coefficient of x»);
double b=ob.nextDouble();
System.out.println(«Enter the constant term»);
double c=ob.nextDouble();
double dis=b*b-4*a*c;
if(dis>0)
System.out.println(«The equation has 2 real and distinct solutions.»);
double root1=(-b+Math.sqrt(dis))/(2*a);
double root2=(-b-Math.sqrt(dis))/(2*a);
System.out.println(«Root 1 is : «+root1);
System.out.println(«Root 2 is : «+root2);
>
else if(dis==0)
System.out.println(«The equation has 2 real and equal solutions.»);
double root=(-b+Math.sqrt(dis))/(2*a);
System.out.println(«The equal Root is : «+root);
>
else
System.out.println(«The equation has no real solution.It has only imaginary solution.»);
System.out.println(«No solution can be represented here.»);
>
>
>

This very simple program inputs the quadratic equation by inputting the coefficients of x2 ,x and constant term.

After that the value of discriminant is calculated by its formula Discriminant=b2-4ac.

As we know that the roots of a Quadratic equation depends largely on the value of discriminant ,three cases occur.If discriminant is grater than zero than two distinct and real roots are obtained , which are calculated and given by Dharacharya formula.

If discriminant is zero then it means that the equation is a Perfect Square and two equal roots are obtained.

If discriminant is less than zero then no real roots are obtained and thus it has no real solution and since no datatype of JAVA can hold imaginary value, no solution can be represented here.

Источник

Solving quadratic equation in java

Learn Latest Tutorials

Preparation

Trending Technologies

B.Tech / MCA

Javatpoint Services

JavaTpoint offers too many high quality services. Mail us on h[email protected], to get more information about given services.

• Website Designing
• Website Development
• Java Development
• PHP Development
• WordPress
• Graphic Designing
• Logo
• Digital Marketing
• On Page and Off Page SEO
• PPC
• Content Development
• Corporate Training
• Classroom and Online Training
• Data Entry

Training For College Campus

JavaTpoint offers college campus training on Core Java, Advance Java, .Net, Android, Hadoop, PHP, Web Technology and Python. Please mail your requirement at [email protected].
Duration: 1 week to 2 week

Like/Subscribe us for latest updates or newsletter

Источник

Java: Solve quadratic equations

Java Conditional Statement: Exercise-2 with Solution

Write a Java program to solve quadratic equations (use if, else if and else).

Test Data
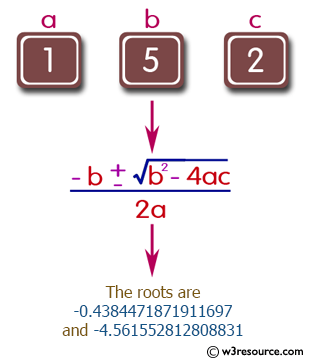
Input a: 1
Input b: 5
Input c: 1

Pictorial Presentation:

Sample Solution:

import java.util.Scanner; public class Exercise2 < public static void main(String[] Strings) < Scanner input = new Scanner(System.in); System.out.print("Input a: "); double a = input.nextDouble(); System.out.print("Input b: "); double b = input.nextDouble(); System.out.print("Input c: "); double c = input.nextDouble(); double result = b * b - 4.0 * a * c; if (result >0.0) < double r1 = (-b + Math.pow(result, 0.5)) / (2.0 * a); double r2 = (-b - Math.pow(result, 0.5)) / (2.0 * a); System.out.println("The roots are " + r1 + " and " + r2); >else if (result == 0.0) < double r1 = -b / (2.0 * a); System.out.println("The root is " + r1); >else < System.out.println("The equation has no real roots."); >> > 

Input a: 1 Input b: 5 Input c: 2 The roots are -0.4384471871911697 and -4.561552812808831

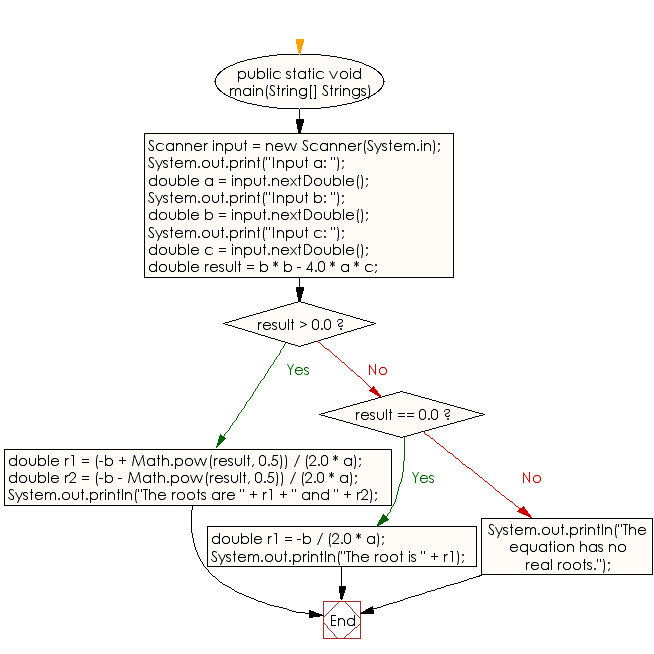
Java Code Editor:

Contribute your code and comments through Disqus.

What is the difficulty level of this exercise?

Test your Programming skills with w3resource’s quiz.

Follow us on Facebook and Twitter for latest update.

Java: Tips of the Day

How to call getClass() from a static method in Java?

Just use TheClassName.class instead of getClass()

• Weekly Trends
• Java Basic Programming Exercises
• SQL Subqueries
• Adventureworks Database Exercises
• C# Sharp Basic Exercises
• SQL COUNT() with distinct
• JavaScript String Exercises
• JavaScript HTML Form Validation
• Java Collection Exercises
• SQL COUNT() function
• SQL Inner Join
• JavaScript functions Exercises
• Python Tutorial
• Python Array Exercises
• SQL Cross Join
• C# Sharp Array Exercises

We are closing our Disqus commenting system for some maintenanace issues. You may write to us at reach[at]yahoo[dot]com or visit us at Facebook

Источник

Discovering Quadratic Equations in Java: A Guide

The roots of a quadratic equation can be calculated using the formula: $$x = \frac<-b\pm\sqrt[]>$$ To do so, first determine the determinant value by computing (b*b)-(4*a*c). Then, set f(x) = 0 to solve the equation ax^2 + bx + c = 0 and find the roots of the quadratic function. The nature of the roots can be determined by the value of the determinant (b^2 – 4ac): if (b^2 – 4ac) > 0, the roots are real and different.

Java program to find the roots of a quadratic equation

The formula used to find the roots of a quadratic equation is as follows:

The quadratic formula, which is used to solve quadratic equations, can be written as follows: $$x = \frac<-b\pm\sqrt[]>$$

• Determine the value of the determinant by subtracting 4*a*c from the square of b.
• In case the determinant exceeds 0, the roots would be [-b + the square root of the determinant] divided by 2 times a, and [-b — the square root of the determinant] divided by 2 times a.
• The root value for a determinant equal to 0 can be calculated using the formula (-b+Math.sqrt(d))/(2*a).

Example

import java.util.Scanner; public class RootsOfQuadraticEquation < public static void main(String args[])< double secondRoot = 0, firstRoot = 0; Scanner sc = new Scanner(System.in); System.out.println("Enter the value of a ::"); double a = sc.nextDouble(); System.out.println("Enter the value of b ::"); double b = sc.nextDouble(); System.out.println("Enter the value of c ::"); double c = sc.nextDouble(); double determinant = (b*b)-(4*a*c); double sqrt = Math.sqrt(determinant); if(determinant>0)< firstRoot = (-b + sqrt)/(2*a); secondRoot = (-b - sqrt)/(2*a); System.out.println("Roots are :: "+ firstRoot +" and "+secondRoot); >else if(determinant == 0) < System.out.println("Root is :: "+(-b + sqrt)/(2*a)); >> >

Output

Enter the value of a :: 15 Enter the value of b :: 68 Enter the value of c :: 3 Roots are :: -0.044555558333472335 and -4.488777774999861

10 Java Program to Find Roots of Quadratic Equation, Java Program to Find Roots of Quadratic Equation | Solve Quadratic Equations using if Duration: 7:49

Java walk through: Quadratic Formula

We walk through implementing a quadratic formula program (in Java + Eclipse) that returns Duration: 18:20

Java Program to Display Roots of Quadratic Equation

quadratic equation java methodwrite a java program with quadratic formulajava program to Duration: 15:01

How to solve a Quadratic Equation in Java

I am opening up a few 1:1 sessions using topmate (https://topmate.io/dinesh_varyani) for Duration: 10:57

Java Program to Find the Roots of Quadratic Equation

The x-intercepts of a function are also known as its roots. Since the points on the x-axis have a y-coordinate of zero, we can determine the roots of a quadratic function by setting f(x) equal to zero and solving the equation ax^2 + bx + c = 0.

Requirements for a quadratic equation —

ax^2 + bx + c = 0 where a, b, c are real numbers and cannot be zero ie, there value must be from and

A mathematical expression to determine the solutions of a quadratic equation —

roots = (-b ± √(b2-4ac)) / (2a)± represents there are two roots.

The solutions of the quadratic equations are given by the roots, which are —

first = (-b + √(b2-4ac)) / (2a) second = (-b - √(b2-4ac)) / (2a)

The determinant, represented as (b^2 — 4ac), provides information about the characteristics of the roots.

1. In case the discriminant (b^2 – 4ac) is greater than zero, the roots of the equation will be both real and distinct.
2. If the discriminant, represented by b^2 — 4ac, equals zero, then the roots of the equation are real and identical.
3. When the value of (b^2 – 4ac) is less than zero, then the roots will be distinct and complex.

Algorithm to determine the solutions of a second-degree polynomial equation:

Java

First Root = -0.35+1.06i Second Root = -0.35-1.06i

How to solve a Quadratic Equation in Java, I am opening up a few 1:1 sessions using topmate (https://topmate.io/dinesh_varyani) for Duration: 10:57

Parsing a quadratic equation in java

To ensure accurate results, it is necessary to keep adding the values for both x^2 and x continuously. The code has been modified and tested successfully.

public class ParseEquation < public static double coeff(String str, String regex) < Pattern patt = Pattern.compile(regex); Matcher match = patt.matcher(str); // missing coefficient default String coeff = "+0"; double value = 0; while(match.find())< coeff = match.group(1); value = value + Double.parseDouble(coeff); >// always have sign, handle implicit 1 return (coeff.length() == 1) ? (value + 1) : value; > public static String[] quadParse(String arg) < String str = ("+" + arg).replaceAll("\\s", ""); double a1 = coeff(str, "([+-]2*)x\\^2"); double b1 = coeff(str, "([+-]6*)x(?!\\^)"); double c1= coeff(str, "([+-]3+)(?!x)"); System.out.println("Values are a: " + a1 + " b: " + b1 + " c: " + c1); double dis = (Math.pow(b1, 2.0)) - (4 * a1 * c1); double d = Math.sqrt(dis); double X = 0, Y = 0; //root 1 & root 2, respectively if (dis >0.0 || dis < 0.0) < X = (-b1 + d) / (2.0 * a1); Y = (-b1 - d) / (2.0 * a1); String root1 = Double.toString(X); String root2 = Double.toString(Y); return new String[]; > else if (dis == 0.0) < X = (-b1 + 0.0) / (2.0 * a1);//repeated root String root2 = Double.toString(X); return new String[]; > return new String[-1]; > public static void main(String[] args) throws IOException < BufferedReader r = new BufferedReader (new InputStreamReader(System.in)); String s; while ((s=r.readLine()) != null) < String[] pieces = quadParse(s); System.out.println(Arrays.toString(pieces)); >> > 

Below is the result that appears when the program is executed:

2x^2 + 2x -3x -25 +15 =0 Values are a: 2.0 b: -1.0 c: -10.0 [2.5, -2.0]

The logic you wrote should be working fine, as I have not made any modifications to it. It is capable of accurately summing the coefficients.

The edited version of the answer now accommodates implicit 1.

Values are a: 1.0 b: -5.0 c: -25.0

The given set of coordinates is [-3.0901699437494745, 8.090169943749475].

public class ParseEquation < public static String coeff(String str, String regex) < Pattern patt = Pattern.compile(regex); Matcher match = patt.matcher(str); // missing coefficient default String coeff = "+0"; double value = 0; if(match.find()) coeff = match.group(1); // always have sign, handle implicit 1 value= Double.parseDouble((coeff.length() == 1) ? coeff + "1" : coeff); while(match.find())< coeff = match.group(1); value = value + Double.parseDouble(coeff); >String value2 =String.valueOf(value); return (value2.length() == 1) ? (value2 + "1") : value2; > public static String[] quadParse(String arg) < String str = ("+" + arg).replaceAll("\\s", ""); double a1 = Double.parseDouble(coeff(str, "([+-]9*)([a-z]\\^2)")); double b1 = Double.parseDouble(coeff(str, "([+-]8*)([a-z](?!\\^))")); double c1= Double.parseDouble(coeff(str, "([+-]9+)(?![a-z])")); System.out.println("Values are a: " + a1 + " b: " + b1 + " c: " + c1); double dis = (Math.pow(b1, 2.0)) - (4 * a1 * c1); double d = Math.sqrt(dis); double X = 0, Y = 0; //root 1 & root 2, respectively if (dis >0.0 || dis < 0.0) < X = (-b1 + d) / (2.0 * a1); Y = (-b1 - d) / (2.0 * a1); String root1 = Double.toString(X); String root2 = Double.toString(Y); return new String[]; > else if (dis == 0.0) < X = (-b1 + 0.0) / (2.0 * a1);//repeated root String root2 = Double.toString(X); return new String[]; > return new String[-1]; > public static void main(String[] args) throws IOException < BufferedReader r = new BufferedReader (new InputStreamReader(System.in)); String s; while ((s=r.readLine()) != null) < String[] pieces = quadParse(s); System.out.println(Arrays.toString(pieces)); >> > 

Java Quadratic Equation Class, Implement a class QuadraticEquation whose constructor receives the coefficients a, b, c of the quadratic equation. Supply methods getSolution1

Java Quadratic Equation Class

Your issue arises from inputting 0, 0, 0 when creating the class instance. To resolve this, modify the class creation line accordingly.

QuadraticFormula form = new QuadraticFormula(Coefficient A, b. ) 

Apologies for the formatting, I am using my phone. However, the user’s input coefficient should be placed into the arguments via the scanner input.

The reason for the squiggly lines underneath coeffA = in.nextDouble(); coeffB = in.nextDouble(); and coeffC = in.nextDouble(); is that you have assigned something to them but failed to utilize them.

It is recommended to replace QuadraticEquation equation = new QuadraticEquation(0, 0, 0); with QuadraticEquation equation = new QuadraticEquation(coeffA, coeffB, coeffC); .

The incorrect placement of parentheses in getSolution techniques is leading to the wrong order of calculations being performed.

(-coeffB + Math.sqrt(discriminant)) / (2 * coeffA) 

(-coeffB - Math.sqrt(discriminant)) / (2 * coeffA) 

Your if statements are incorrect and need revision. In the case of real solutions, you should print both solutions. However, if there are no real solutions, you should indicate this in the output.

if (equation.hasSolutions()) < System.out.println(equation.getSolution1()); System.out.println(equation.getSolution2()); >else

Java Program to Display Roots of Quadratic Equation, quadratic equation java methodwrite a java program with quadratic formulajava program to Duration: 15:01

How do you find the quadratic equation in Java?

This Java code aims to determine the roots of a quadratic equation. Firstly, it calculates the determinant value, which is represented as (b*b)-(4*a*c). If the determinant is greater than zero, then the roots will be (-b +squareroot(determinant)]/2*a and [-b -squareroot(determinant)]/2*a. On the other hand, if the determinant is equal to zero, then the root value will be (-b+Math.sqrt(d))/(2*a).

How do you solve equations in Java?

The given code is an example of a Java program that can be used to solve linear equations. It makes use of a Scanner class and defines a Solve_Linear_Equation class with a main method. The program prompts the user to enter the number of variables in the equations, which are stored as characters in an array called var.

How do you find the roots in Java?

The Math class in Java provides two ways to calculate the square root of a number. The first method is to use the sqrt() function, which takes a double as an argument and returns the square root of that number. For example, if we want to calculate the square root of 9, we can use the sqrt() function as follows: double R = Math.sqrt(9); We can then print the result using the System.out.println() function. The second method is to use the pow() function, which takes two arguments: the base (in this case, X) and the exponent (0.5, which is equivalent to the square root). For example: double R = Math.pow(X, 0.5); Once again, we can print the result using the System.out.println() function. Both methods will give us the same result: The square root of 9 is 3.0.

How do you write an equation in Java?

The Java language offers several useful methods for mathematical operations. For instance, the Math.max(x,y) method can be utilized to determine the highest value between two variables, while the Math.min(x,y) method can be used to determine the lowest value between them. Additionally, the Math.sqrt(x) method can be applied to calculate the square root of a given number, and the Math.abs(x) method can be used to find the absolute value of a number.

Источник