Алгоритмическая сложность
Алгоритмическая сложность — тема отдельного курса в классических университетских программах. Как, впрочем, и математический анализ. Однако на собеседовании Вас вряд ли попросят посчитать интеграл, а вот про сложность алгоритмов спрашивают практически всех на любую позицию программиста. А знакомо ли Вам понятие алгоритмическая сложность? А какая сложность быстрой сортировки? А это в лучшем или в худшем случае? Бывает, с горем пополам разобрались с какой-нибудь задачей на логику, но вас добивают: а какая сложность Вашего решения, можно ли ускорить? В этом посте постараюсь объяснить, что тут к чему, и не пугайтесь, если для Вас NP-полнота значит не больше, чем NP-пустота.
Важность понятия алгоритмической сложности в том, что на практике, как правило, существует разумно оптимальный способ решить задачу. Использовав его, дальнейшая оптимизация будет улучшать производительность на 10-50%, что потребует ещё в два или пять раз больше времени на разработку. Одновременно с этим, неправильно выбранный способ решения будет работать медленнее в десять, в сто, в тысячу раз. На практике система виснет на простых операциях, загрузка занимает секунды, а всевозможные запланированные задачи запускаются по ночам и работают часами. И объёмы данных отнюдь не терабайты, достаточно нескольких миллионов записей. И я расскажу, почему.
Сложность алгоритма — это ответ на вопрос сколько действий придётся совершить, чтобы решить задачу, в зависимости от параметров задачи. Разнородных параметров в задаче может быть много, и разнородных действий тоже. И то и другое нужно сократить до одного: один параметр и одно действие, остальное отбросить. Например, Вы листаете договор из тысячи страниц и подписываете каждую. Входной параметр такой задачи будет количество страниц, а действие — поставить подпись. Перелистывание страниц мы не считаем за важное действие, потому что это намного быстрее подписи. Не важно, сколько времени уйдёт на всё, два часа или два дня — кто-то расписывается быстрее, кто-то медленнее. Но каждому потребуется 1000 действий для выполнения алгоритма. Если обобщить, то требуется N действий при N страницах. Легко можно посчитать, что если Вы подписали договор из 10 страницы за 10 минут, то на 60 страниц Вы потратите час. Если оптимизировать процесс и подписывать только первую страницу, то потребуется одна минута вне зависимости от количества страниц.
Другой пример — на бумаге разлинован квадрат со стороной 10. В каждой клетке нужно поставить точку, всего точек 100 (N^2). Если потребовалось 10 минут на всё про всё, то, чтобы повторить алгоритм на квадрате со стороной 60, потребуется 10 / 100 * 60 * 60 = 360 минут, то есть 6 часов. Итого в одной задаче увеличив входной параметр в шесть раз, мы потратили в 6 раз больше времени, а в другой — в 36. Разница колоссальная.
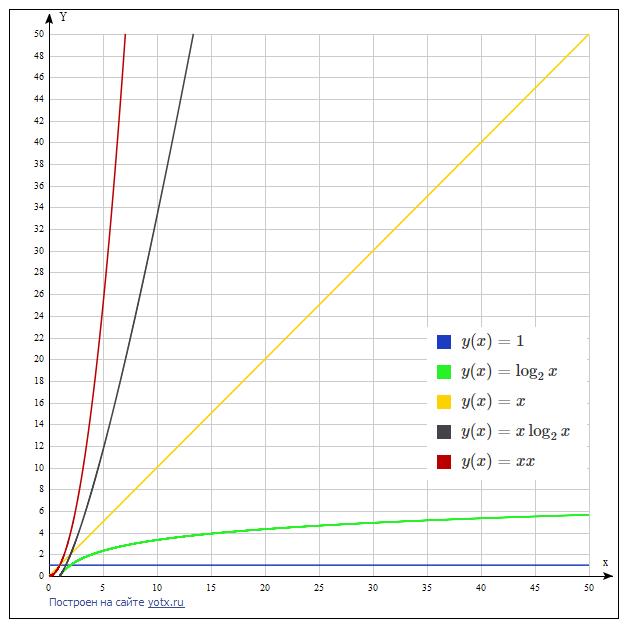
Я привёл три примера сложности алгоритма: константную, порядка N и порядка N^2. У программистов принято говорить «О большое от». Ниже для порядка я приведу строгое определение, но на практике требуется лишь указать порядок скорости роста времени работы алгоритма при росте основного параметра задачи. Коэффициент перед функцией от N не важен: если требуется N^2 действие или 100 * N^2 действий — это всё равно будет O(N^2), потому что в обоих случаях рост N в два раза увеличивает время работы в четыре.
«O»-обозначение используется, если нужно определить асимптотическую верхнюю границу для функции f(n), равную времени работы алгоритма в зависимости от основного параметра задачи.
//before java8 for (IteratorString> iterator = elements.iterator(); iterator.hasNext(); ) String next = iterator.next(); if(Long.parseLong(next) % 2 == 1) iterator.remove(); > > Но на собеседованиях часто даются такие задачи с небольшим подвохом, чтобы проверить понимание нюансов. Решения исходной задачи:
//java8 AtomicInteger counter = new AtomicInteger(0); elements.removeIf(s -> counter.incrementAndGet() % 2 == 0); //before java8 int counter = 0; for (IteratorString> iterator = elements.iterator(); iterator.hasNext(); ) iterator.next(); if (counter++ % 2 == 1) iterator.remove(); > > //before java8 //хитрый способ избежать введения переменной counter. Следует избегать таких неочевидных приёмов. for (ListIteratorString> literator = elements.listIterator(elements.size()); literator.hasPrevious();) literator.previous(); if (literator.previousIndex() % 2 == 0) literator.remove(); > > //O(n) for ArrayList //решение на крайний случай, если вероятны проблемы с производительностью, но от ArrayList не уйти. //объём кода не соответствует сложности задачи, читаемость его тоже низкая, придётся объяснять в комментариях, //почему так, а не иначе //если применить это решение к LinkedList, то получим O(n^2) removeFromArrayList(elements, i -> i % 2 == 1); static void removeFromArrayList(ArrayListString> elements, IntPredicate removeIf) int lastIndex = 0; for (int i = 0; i elements.size(); i++) if (!removeIf.test(i)) elements.set(lastIndex, elements.get(i)); lastIndex++; > > int extraElementsCount = elements.size() - lastIndex; //unfortunately, we can't use protected removeRange method for (int i = 0; i extraElementsCount; i++) elements.remove(elements.size() - 1); > > Прокомментирую решения, предложенные на stackoverflow.
//1. //Корректное решение. O(n^2) для ArrayList, O(n) для LinkedList int i = 0; for (IteratorString> it = words.iterator(); it.hasNext(); ) it.next(); // Add this line in your code if (i % 2 != 0) it.remove(); > i++; > //2. //Некорректное решение. O(n^2) для ArrayList, O(n^2) для LinkedList. //Ошибочный результат при дублирующихся значениях в списке. int i = 0; ListString> list = new ArrayListString>(); for (String word:words) if (i % 2 != 0) //it.remove(); list.add(word); > i++; > words.removeAll(list); //элементы удаляются по значению! //додумать решение можно так (ещё заменить условие на ==0): //words.clear(); //words.addAll(list); //3. //На этом примере я потерпел фиаско. Я был уверен, что код не работает, потому что размер и индексы будут изменяться по ходу работы алгоритма, //что, удаляя элемент с индексом 2, мы удаляем элемент с индексом 3 в исходном массиве. Всё перепуталось и не может дать верный результат. //Но! результат верный. На каждом шагу мы удаляем элемент, сдвигаем все индексы на 1 влево, но увеличиваем счётчик на 1, а не на 2. //здесь мои полномочия всё, как говорится //Сложность O(n^2) для ArrayList и LinkedList int i = 1; while (i words.size()) words.remove(i++); > //4. //Корректное решение. Единственное из предложенных O(n) для ArrayList; O(n^2) для LinkedList. //Минус - тяжело читаемый код. Два счётчика, называются i, j. Причём j всегда равно i/2. //Если это писали не Вы, то придётся запускать отладку, чтобы разобраться. int j = 0; for(int i = 0 ; i integers.size(); i++) if( i % 2 == 0) integers.set(j, integers.get(i)); j++; > > int half = integers.size()%2==0 ? integers.size()/2 : integers.size()/2 + 1; integers.subList(half , integers.size()).clear();//буду знать, что subList не создаёт новый список, а лишь ссылку на подсписок текущего. //поэтому хвост можно обрезать вот так в одну строчку. Пример с удалением один из самых базовых и простых. Подобным образом можно мусолить любые коллекции и операции с ними: LinkedList, ArrayList, HashMap, TreeMap, LinkedHashMap, CopyOnWriteArrayList и так далее. В данном посте я этого делать не буду, перейду к итогу всего что я тут понаписал.
Заключение
Приходится соблюдать тонкий баланс между оптимальностью решения по производительности, читаемостью и лаконичностью кода и здравым смыслом. Главное понимать насколько быстро можно решить типовую задачу и подобрать правильные структуры данных и операции с ними. На интервью на позицию Java разработчика часто вопрос по данной тематике будет вторым (после «методов класса Object» или «расскажите о последнем проекте»).
Big O — Java: Массивы
Когда заходит речь про алгоритмы, нельзя не упомянуть понятие «сложность алгоритма» (обозначается как Big O). Оно дает понимание того, насколько эффективен алгоритм.
Как вы помните, алгоритмов сортировок существует много. Все они выполняют одну и ту же задачу, но при этом отличаются друг от друга. В информатике алгоритмы сравниваются друг с другом по их алгоритмической сложности. Эта сложность оценивается как количество выполняемых операций алгоритмом для достижения своей цели. Например разные способы сортировки требуют очень разного количества «проходов» по массиву перед тем как массив будет полностью отсортирован. Понятно, что конкретное количество операций зависит от входных данных, например, если массив уже отсортирован, то количество операций будет минимальным (но они все равно будут, потому что алгоритм должен убедиться в том, что массив отсортирован).
Big O как раз придумана для описания алгоритмической сложности. Она призвана показать, как сильно увеличится количество операций при увеличении размера данных.
Вот некоторые примеры того, как записывается сложность: O(1), O(n), O(nlog(n)).
O(1) описывает константную (постоянную) сложность. Такой сложностью обладает операция доступа к элементу массива по индексу. Сложность (в алгоритмическом смысле) доступа к элементу не зависит от размеров массива и является величиной постоянной. А вот функция, которая печатает на экран все элементы переданного массива, используя обычный перебор, имеет сложность O(n) (линейная сложность). То есть количество выполняемых операций, в худшем случае, будет равно количеству элементов массива. Именно это количество символизирует символ n в скобках.
Что такое худший случай? В зависимости от того в каком состоянии находятся начальный массив, количество операций будет разным даже при условии, что массив одного и того же размера. Чтобы проще понять, возьмем в качестве аналогии Кубик Рубика. Количество операций (действий) которые нужно проделать для сборки Кубика Рубика зависит от того, в каком положении находятся его грани перед сборкой. В некоторых случаях действий понадобится мало, в других много. И вот та ситуация, в которой таких действий понадобится больше всего и называется худшим случаем. Алгоритмическая сложность всегда оценивается по худшему случаю для выбранного алгоритма.
Еще один пример — вложенные циклы. Вспомните как работает поиск пересечений в неотсортированных массивах. Для каждого элемента из одного массива проверяется каждый элемент другого массива (либо через цикл, либо с помощью метода includes() , чья сложность O(n), ведь в худшем случае он просматривает весь массив). Если принять, что размеры обоих массивов одинаковы и равны n, то получается, что поиск пересечений имеет квадратичную сложность или O(n^2) (n в квадрате).
Существуют как очень эффективные, так и абсолютно неэффективные алгоритмы. Скорость работы подобных алгоритмов падает с катастрофической скоростью даже при небольшом количестве элементов. Нередко более быстрые алгоритмы быстрее не потому, что они лучше, а потому что они потребляют больше памяти или имеют возможность запускаться параллельно (и если это происходит, то работают крайне эффективно). Как и все в инженерной деятельности, эффективность — компромисс. Выигрывая в одном месте, мы проиграем где-то в другом.
Big O, во многом, теоретическая оценка, на практике все может быть по-другому. Реальное время выполнения зависит от множества факторов среди которых: архитектура процессора, операционная система, язык программирования, доступ к памяти (последовательный или произвольный) и многое другое.
Вопрос эффективности кода довольно опасен. В силу того, что многие начинают учить программирование именно с алгоритмов (особенно в университете), им начинает казаться, что эффективность — это главное. Код должен быть быстрым.
Такое отношение к коду гораздо чаще приводит к проблемам, чем делает его лучше. Важно понимать, что эффективность — враг понимаемости. Такой код всегда сложнее, больше подвержен ошибкам, труднее модифицируется, дольше пишется. А главное, настоящая эффективность редко когда нужна сразу или вообще не нужна. Обычно тормозит не код, а, например, запросы к базе данных или сеть. Но даже если код выполняется медленно, то вполне вероятно, что именно тот участок, который вы пытаетесь оптимизировать, вызывается за все время жизни программы всего лишь один раз и ни на что не влияет, потому что работает с небольшим объемом памяти, а где-то в это время есть другой кусок, который вызывается тысячи раз, и приводит к реальному замедлению.
Открыть доступ
Курсы программирования для новичков и опытных разработчиков. Начните обучение бесплатно