- Shell Sort Algorithm
- Working of Shell Sort
- Shell Sort Algorithm
- Shell Sort Complexity
- Time Complexity
- Space Complexity:
- Shell Sort Applications
- Other Sorting Algorithms
- Table of Contents
- Shell Sort Algorithm
- Working of Shell Sort
- Shell Sort Algorithm
- Shell Sort Code in Python, Java, and C/C++
- Shell Sort Complexity
- Time Complexity
- Space Complexity:
- Shell Sort Applications
- Other Sorting Algorithms
- Table of Contents
- Free Courses on YouTube
Shell Sort Algorithm
Shell sort is a generalized version of the insertion sort algorithm. It first sorts elements that are far apart from each other and successively reduces the interval between the elements to be sorted.
The interval between the elements is reduced based on the sequence used. Some of the optimal sequences that can be used in the shell sort algorithm are:
- Shell’s original sequence: N/2 , N/4 , …, 1
- Knuth’s increments: 1, 4, 13, …, (3 k – 1) / 2
- Sedgewick’s increments: 1, 8, 23, 77, 281, 1073, 4193, 16577. 4j+1+ 3·2j+ 1
- Hibbard’s increments: 1, 3, 7, 15, 31, 63, 127, 255, 511…
- Papernov & Stasevich increment: 1, 3, 5, 9, 17, 33, 65.
- Pratt: 1, 2, 3, 4, 6, 9, 8, 12, 18, 27, 16, 24, 36, 54, 81.
Note: The performance of the shell sort depends on the type of sequence used for a given input array.
Working of Shell Sort
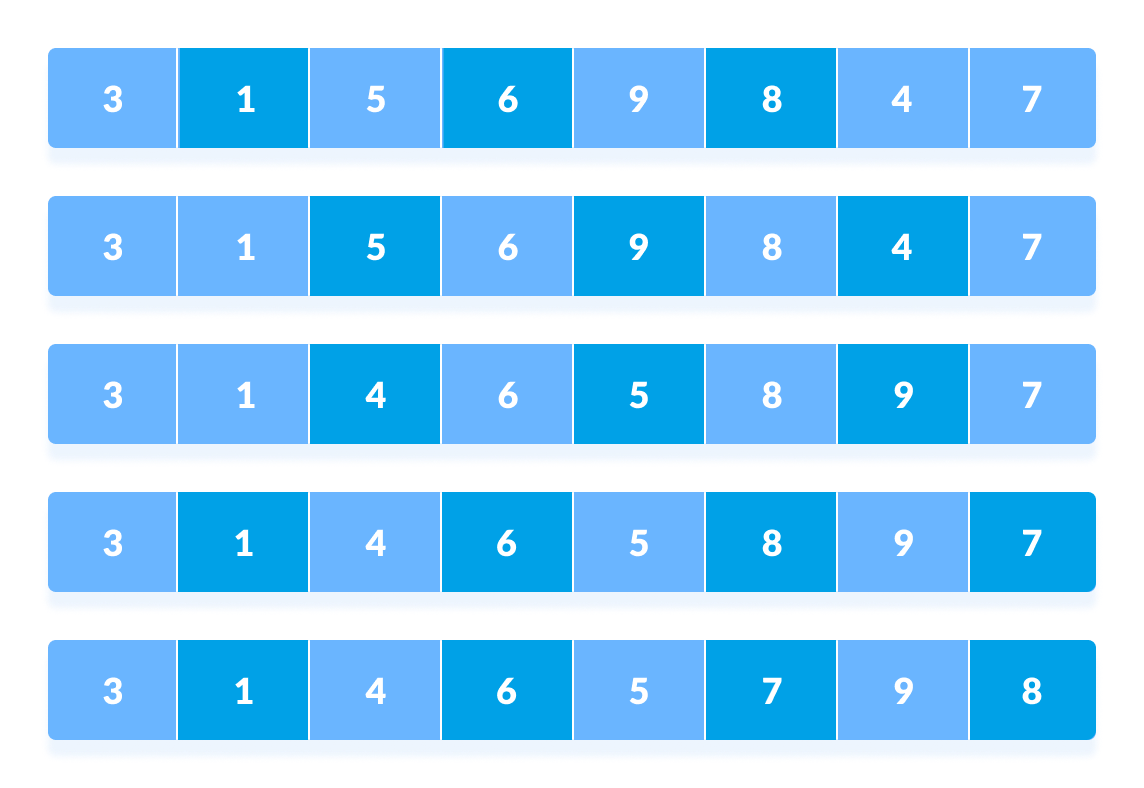
- Suppose, we need to sort the following array.
- We are using the shell’s original sequence (N/2, N/4, . 1 ) as intervals in our algorithm.
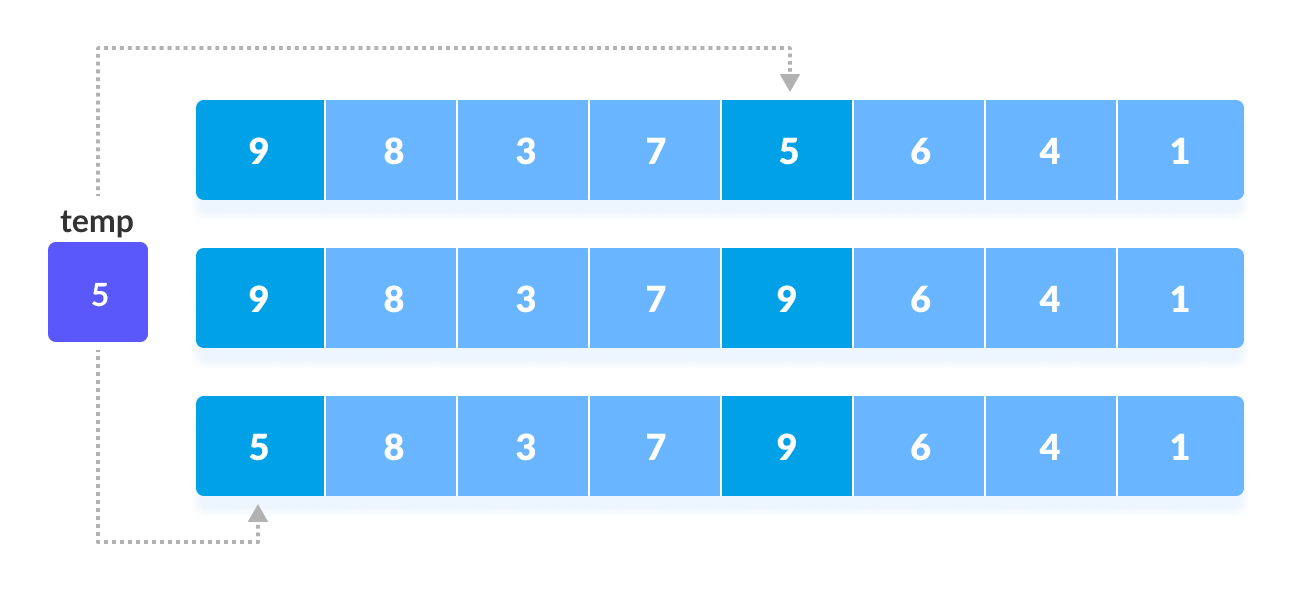
In the first loop, if the array size is N = 8 then, the elements lying at the interval of N/2 = 4 are compared and swapped if they are not in order.
- The 0th element is compared with the 4th element.
- If the 0th element is greater than the 4th one then, the 4th element is first stored in temp variable and the 0th element (ie. greater element) is stored in the 4th position and the element stored in temp is stored in the 0th position.
This process goes on for all the remaining elements.
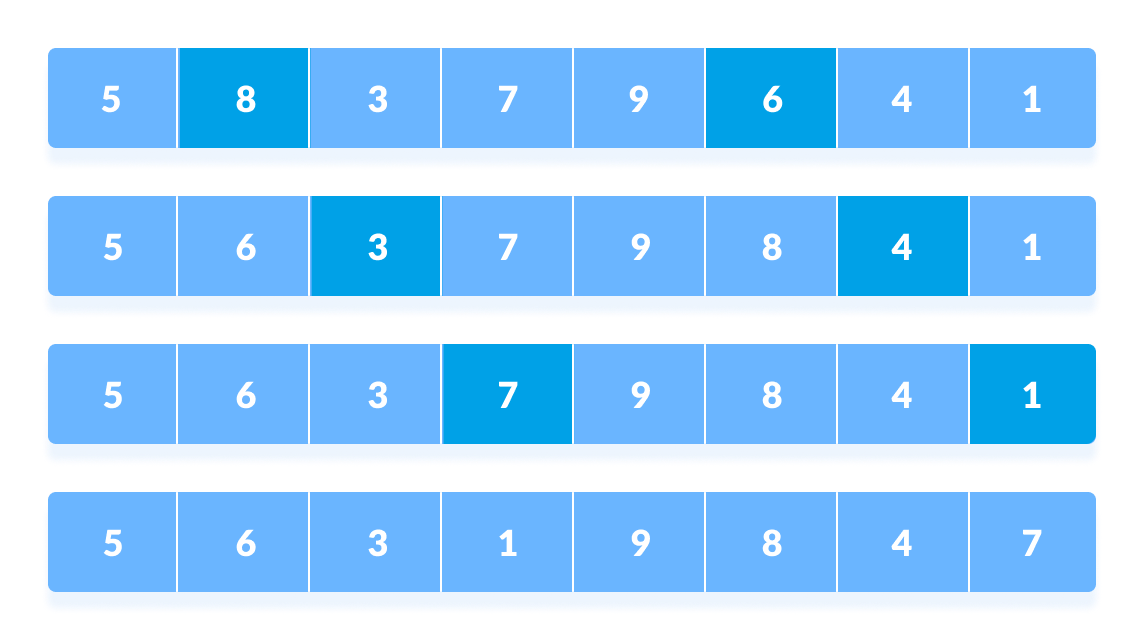
You might get confused at this point.
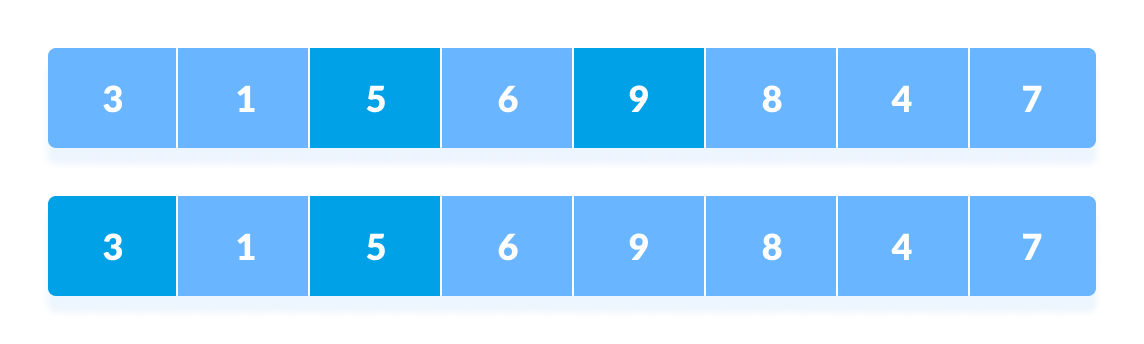
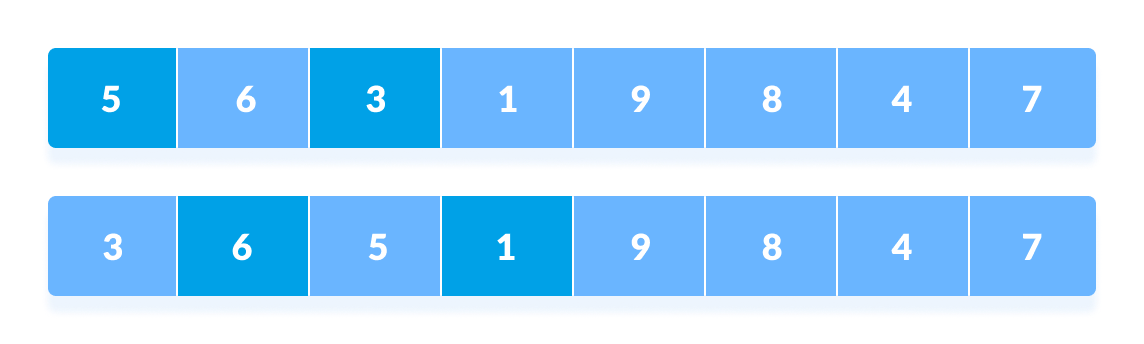
The elements at 4th and 2nd position are compared. The elements at 2nd and 0th position are also compared. All the elements in the array lying at the current interval are compared.

Shell Sort Algorithm
shellSort(array, size) for interval i Shell Sort Code in Python, Java, and C/C++
# Shell sort in python def shellSort(array, n): # Rearrange elements at each n/2, n/4, n/8, . intervals interval = n // 2 while interval > 0: for i in range(interval, n): temp = array[i] j = i while j >= interval and array[j - interval] > temp: array[j] = array[j - interval] j -= interval array[j] = temp interval //= 2 data = [9, 8, 3, 7, 5, 6, 4, 1] size = len(data) shellSort(data, size) print('Sorted Array in Ascending Order:') print(data)// Shell sort in Java programming import java.util.Arrays; // Shell sort class ShellSort < // Rearrange elements at each n/2, n/4, n/8, . intervals void shellSort(int array[], int n) < for (int interval = n / 2; interval >0; interval /= 2) < for (int i = interval; i < n; i += 1) < int temp = array[i]; int j; for (j = i; j >= interval && array[j - interval] > temp; j -= interval) < array[j] = array[j - interval]; >array[j] = temp; > > > // Driver code public static void main(String args[]) < int[] data = < 9, 8, 3, 7, 5, 6, 4, 1 >; int size = data.length; ShellSort ss = new ShellSort(); ss.shellSort(data, size); System.out.println("Sorted Array in Ascending Order: "); System.out.println(Arrays.toString(data)); > >// Shell Sort in C programming #include // Shell sort void shellSort(int array[], int n) < // Rearrange elements at each n/2, n/4, n/8, . intervals for (int interval = n / 2; interval >0; interval /= 2) < for (int i = interval; i < n; i += 1) < int temp = array[i]; int j; for (j = i; j >= interval && array[j - interval] > temp; j -= interval) < array[j] = array[j - interval]; >array[j] = temp; > > > // Print an array void printArray(int array[], int size) < for (int i = 0; i < size; ++i) < printf("%d ", array[i]); >printf("\n"); > // Driver code int main() < int data[] = ; int size = sizeof(data) / sizeof(data[0]); shellSort(data, size); printf("Sorted array: \n"); printArray(data, size); >// Shell Sort in C++ programming #include using namespace std; // Shell sort void shellSort(int array[], int n) < // Rearrange elements at each n/2, n/4, n/8, . intervals for (int interval = n / 2; interval >0; interval /= 2) < for (int i = interval; i < n; i += 1) < int temp = array[i]; int j; for (j = i; j >= interval && array[j - interval] > temp; j -= interval) < array[j] = array[j - interval]; >array[j] = temp; > > > // Print an array void printArray(int array[], int size) < int i; for (i = 0; i < size; i++) cout // Driver code int main() < int data[] = ; int size = sizeof(data) / sizeof(data[0]); shellSort(data, size); cout
Shell Sort Complexity
| Time Complexity | |
|---|---|
| Best | O(nlog n) |
| Worst | O(n 2 ) |
| Average | O(nlog n) |
| Space Complexity | O(1) |
| Stability | No |
Shell sort is an unstable sorting algorithm because this algorithm does not examine the elements lying in between the intervals.
Time Complexity
- Worst Case Complexity: less than or equal to O(n 2 )
Worst case complexity for shell sort is always less than or equal to O(n 2 ) .
The complexity depends on the interval chosen. The above complexities differ for different increment sequences chosen. Best increment sequence is unknown.
Space Complexity:
The space complexity for shell sort is O(1) .
Shell Sort Applications
- calling a stack is overhead. uClibc library uses this sort.
- recursion exceeds a limit. bzip2 compressor uses it.
- Insertion sort does not perform well when the close elements are far apart. Shell sort helps in reducing the distance between the close elements. Thus, there will be less number of swappings to be performed.
Other Sorting Algorithms
Table of Contents
Shell Sort Algorithm
In this tutorial, you will learn about the shell sort algorithm and its implementation in Python, Java, C, and C++.
Shell sort is a generalized version of the insertion sort algorithm. It first sorts elements that are far apart from each other and successively reduces the interval between the elements to be sorted.
The interval between the elements is reduced based on the sequence used. Some of the optimal sequences that can be used in the shell sort algorithm are:
- Shell's original sequence: N/2 , N/4 , …, 1
- Knuth's increments: 1, 4, 13, …, (3 k – 1) / 2
- Sedgewick's increments: 1, 8, 23, 77, 281, 1073, 4193, 16577. 4j+1+ 3·2j+ 1
- Hibbard's increments: 1, 3, 7, 15, 31, 63, 127, 255, 511…
- Papernov & Stasevich increment: 1, 3, 5, 9, 17, 33, 65.
- Pratt: 1, 2, 3, 4, 6, 9, 8, 12, 18, 27, 16, 24, 36, 54, 81.
Note: The performance of the shell sort depends on the type of sequence used for a given input array.
Working of Shell Sort
- Suppose, we need to sort the following array.
- We are using the shell's original sequence (N/2, N/4, . 1 ) as intervals in our algorithm.
In the first loop, if the array size is N = 8 then, the elements lying at the interval of N/2 = 4 are compared and swapped if they are not in order.
- The 0th element is compared with the 4th element.
- If the 0th element is greater than the 4th one then, the 4th element is first stored in temp variable and the 0th element (ie. greater element) is stored in the 4th position and the element stored in temp is stored in the 0th position.
This process goes on for all the remaining elements.

You might get confused at this point.

The elements at 4th and 2nd position are compared. The elements at 2nd and 0th position are also compared. All the elements in the array lying at the current interval are compared.


Shell Sort Algorithm
shellSort(array, size) for interval i 2n down to 1 for each interval "i" in array sort all the elements at interval "i" end shellSortShell Sort Code in Python, Java, and C/C++
# Shell sort in python def shellSort(array, n): # Rearrange elements at each n/2, n/4, n/8, . intervals interval = n // 2 while interval > 0: for i in range(interval, n): temp = array[i] j = i while j >= interval and array[j - interval] > temp: array[j] = array[j - interval] j -= interval array[j] = temp interval //= 2 data = [9, 8, 3, 7, 5, 6, 4, 1] size = len(data) shellSort(data, size) print('Sorted Array in Ascending Order:') print(data)// Shell sort in Java programming import java.util.Arrays; // Shell sort class ShellSort < // Rearrange elements at each n/2, n/4, n/8, . intervals void shellSort(int array[], int n) < for (int interval = n / 2; interval > 0; interval /= 2) < for (int i = interval; i < n; i += 1) < int temp = array[i]; int j; for (j = i; j >= interval && array[j - interval] > temp; j -= interval) < array[j] = array[j - interval]; >array[j] = temp; > > > // Driver code public static void main(String args[]) < int[] data = < 9, 8, 3, 7, 5, 6, 4, 1 >; int size = data.length; ShellSort ss = new ShellSort(); ss.shellSort(data, size); System.out.println("Sorted Array in Ascending Order: "); System.out.println(Arrays.toString(data)); > >// Shell Sort in C programming #include // Shell sort void shellSort(int array[], int n) < // Rearrange elements at each n/2, n/4, n/8, . intervals for (int interval = n / 2; interval > 0; interval /= 2) < for (int i = interval; i < n; i += 1) < int temp = array[i]; int j; for (j = i; j >= interval && array[j - interval] > temp; j -= interval) < array[j] = array[j - interval]; > array[j] = temp; > > > // Print an array void printArray(int array[], int size) < for (int i = 0; i < size; ++i) < printf("%d ", array[i]); > printf("\n"); > // Driver code int main() < int data[] = 9, 8, 3, 7, 5, 6, 4, 1>; int size = sizeof(data) / sizeof(data[0]); shellSort(data, size); printf("Sorted array: \n"); printArray(data, size); >// Shell Sort in C++ programming #include using namespace std; // Shell sort void shellSort(int array[], int n) < // Rearrange elements at each n/2, n/4, n/8, . intervals for (int interval = n / 2; interval > 0; interval /= 2) < for (int i = interval; i < n; i += 1) < int temp = array[i]; int j; for (j = i; j >= interval && array[j - interval] > temp; j -= interval) < array[j] = array[j - interval]; > array[j] = temp; > > > // Print an array void printArray(int array[], int size) < int i; for (i = 0; i < size; i++) cout array[i] " "; cout endl; > // Driver code int main() < int data[] = 9, 8, 3, 7, 5, 6, 4, 1>; int size = sizeof(data) / sizeof(data[0]); shellSort(data, size); cout "Sorted array: \n"; printArray(data, size); >Shell Sort Complexity
| Time Complexity | |
|---|---|
| Best | O(nlog n) |
| Worst | O(n 2 ) |
| Average | O(nlog n) |
| Space Complexity | O(1) |
| Stability | No |
Shell sort is an unstable sorting algorithm because this algorithm does not examine the elements lying in between the intervals.
Time Complexity
- Worst Case Complexity: less than or equal to O(n 2 )
Worst case complexity for shell sort is always less than or equal to O(n 2 ) .
The complexity depends on the interval chosen. The above complexities differ for different increment sequences chosen. Best increment sequence is unknown.
Space Complexity:
The space complexity for shell sort is O(1) .
Shell Sort Applications
- calling a stack is overhead. uClibc library uses this sort.
- recursion exceeds a limit. bzip2 compressor uses it.
- Insertion sort does not perform well when the close elements are far apart. Shell sort helps in reducing the distance between the close elements. Thus, there will be less number of swappings to be performed.
Other Sorting Algorithms
Table of Contents
Free Courses on YouTube
Python Full Course Playlist
105 STL Algorithms in Less Than an Hour
C++ STL Playlist
Learn Node.js
Learn Data Science Full course
Learn Computer Networking Full course