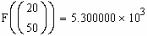«Решение задач линейного программирования (лп)»
Методы линейного программирования получили широкое распространение при решении практических задач, связанных с составлением оптимальных производственных планов, графиков обслуживания потребителей, оптимальным распределением ресурсов, транспортных потоков, размещением оборудования, с составлением различного рода смесей и т.д.
В большинстве оптимизационных задач зависимости между переменными xiлинейны. Линейность математической модели предполагает наличие у нее свойств пропорциональности и аддитивности.
Свойство пропорциональностьозначает то, что вклад каждой переменной в целевую функцию ЦФ и общий объем потребления соответствующих ресурсов прямо пропорционален уровню (величине) этой переменной.
Аддитивностьзаключается в том, что целевая функция ЦФ представляет собой сумму вкладов от различных переменных. Аналогично левая часть каждого ограничения должна представлять собой сумму расходов, каждое слагаемое которой пропорционально величине соответствующей переменной. Если, например, фирма, производит два конкурирующих вида продукции, увеличение сбыта одного из которых отрицательно сказывается на объеме реализации другого, то такая модель не обладает свойством аддитивности.
Математическая модель задачи линейного программирования (ЛП) в достаточно общем случае формулируется следующим образом:
при следующих ограничениях на вектор искомых переменных x=i>:
Для решения задач ЛП различных типов с помощью компьютерных средств удобно использовать математический пакет Mathcadи табличный процессорExcel.Ниже рассматриваются примеры решения типовых задач ЛП с применением этих программных средств.
В среде Mathcad решение задачи ЛП находится в рамках так называемых вычислительных блоков (начинаются с ключевого словаGiven) с использованием встроенных функцийMminimizeилиMaximizeдля минимизации или минимизации целевой функции. В прилагаемых примерах приведены решения нескольких типовых задач, в которых показано, что и как должно быть введено для получения решения. Целевую функцию и ограничения можно записывать в виде отдельных выражений, а также и в векторно-матричной форме, которая является лишь более удобной и компактной формой записи условий задачи ЛП.
В пакете Excel задачи ЛП решают с помощью встроенной функции «Поиск решения».
А. Одноиндексные задачи ЛП
Пример А.1. Решение одноиндексной задачи ЛП в Mathcad
Пример А.2. Решение одноиндексной задачи ЛП в Mathcad
Пример А.3. Задача планирования объемов производства
Задача №1. Фирма производит изделия двух видов A1 и A2 с помощью последовательной обработки каждой из них в трех цехах. Исходные данные задачи приведены в таблице:
Нормы затрат времени на 1 изделие, час/сут
Определить количества xj, j = 1,2 , изделий Aj , которые необходимо изготовить для достижения максимальной прибыли
т.е. найти оптимальный план суточного выпуска изделий А1 и А2. Это типичная задача производственного планирования.
Отметим, что значения x1и x2не могут быть выбраны произвольно, так как существуют ограничения на суточное время работы в цехах. Эти ограничения записываются в виде:
Кроме того значения x1и x2не могут быть отрицательными:
Требуется найти такое неотрицательное решение x1, x2системы линейных неравенств (3.2), при котором целевая функция (3.1) принимает максимальное значение.
Решение одноиндексной Задачи №1 в системе Mathcad
Описание ограничений в матричном виде:
— матрица Мсодержит коэффициенты при неизвестных в левой части ограничений, а векторv— правые части исходных неравенств:
M:=

Решим задачу с помощью вычислительного блока
Для формирования нулевого приближения полагаем значение х2равным нулю (инициализация решения)
x2 := 0
M*x ≤ v x ≥ 0
Таким образом, точка максимума целевой функции F имеет координаты x1 = 20, x2 = 50, а значение ее значение в точке максимума:
.
Решение одноиндексной Задачи 1 в пакете Excel
Для решения оптимизационных задач в табличном процессоре Excelиспользуется пункт «Поиск решения» (Solver – Решатель) в меню «Сервис» на панели инструментов. Если этого пункта нет, то необходимо установить соответствующую надстройку. Для этого в менюСервиснужно выбрать пунктНадстройкии в диалоговом окне установить флажок слева от надписи «Поиск решения». В меню «Сервис» появится пункт «Поиск решения».
Решение.В соответствии сисходнымиданнымиЗадачи 1составим и заполним вExcel следующую таблицу
Числа в ячейках столбца «Ограничения»подсчитаны с помощью формул. Формула=СУММПРОИЗВ(В3:С3;$B$7:$C$7)-D3введена в ячейкуF3и продолжена в ячейкиF4:F5таблицы.
Эта формула также скопирована в F6, но без вычитаемогоD6. Выделим ячейкуF6 с целевой функцией и вызовем Решатель «Сервис/ Поиск решения». В диалоговом окне укажем: «Установить целевую ячейку:»$F$6, «максимальное значение», «Изменяя ячейки:»$B$7:$C$7, «Ограничения:»$F$3:$F$5
Так как все ограничения имеют одинаковые знаки «», тоздесьони введены блоком. Заметим, что количества xj , j = 1, 2 изделий являютсяцелымичислами. Поэтому необходимо наложить еще одно ограничение:$B$7:$C$7=целое(целочисленная оптимизация).
В окне «Параметры» установим флажки «Линейная модель» и «Неотрицательные значения». Запустим «Выполнить».
Поиск решениявернет результат: х1= 20; х2= 50. Целевая функция равна Fmax = 5300. Этот результат поиска максимума функции F совпадает с результатами, полученными ранее с помощью пакета Mathcad.
Пример А.4. Задача о сплавах
Задача №2. Для изготовления сплава из меди, олова и цинка в качестве сырья используют два сплава тех же металлов, отличающихся составом и стоимостью. Данные об этих сплавах приведены в таблице:
Решение задач линейного программирования
Назначение сервиса . Онлайн-калькулятор предназначен для решения задач линейного программирования симплексным методом путем перехода к КЗЛП и СЗЛП . При этом задача на минимум целевой функции сводятся к задаче на поиск максимума через преобразование целевой функции F*(X) = -F(X) . Также имеется возможность составить двойственную задачу.
- Переход к КЗЛП. Любая ЗЛП вида ax ≤ b , ax ≥ b , ax = b ( F(X) → extr ) сводится к виду ax = b , F(X) → max ;
- Переход к СЗЛП. КЗЛП вида ax = b сводится к виду ax ≤ b , F(X) → max ;
- Решение симплексным методом;
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Инструкция . Выберите количество переменных и количество строк (количество ограничений). Полученное решение сохраняется в файле Word .
Переход от задачи минимизации целевой функции к задаче максимизации
Задача минимизации целевой функции F(X) легко может быть сведена к задаче максимизации функции F*(X) при тех же ограничениях путем введения функции: F*(X) = -F(X) . Обе задачи имеют одно и то же решение X*, и при этом min(F(X)) = -max(F*(X)) .
Проиллюстрируем этот факт графически:
| F(x) → min | F(x) → max |
Для оптимизации функции цели используем следующие понятия и методы.
Опорный план – план с определёнными через свободные базисными переменными.
Базисный план – опорный план с нулевыми базисными переменными.
Оптимальный план – базисный план, удовлетворяющий оптимальной функции цели (ФЦ).
Ведущий (разрешающий) элемент – коэффициент свободной неизвестной, которая становится базисной, а сам коэффициент преобразуется в единицу.
Направляющая строка – строка ведущего элемента, в которой расположена с единичным коэффициентом базисная неизвестная, исключаемая при преобразовании (строка с минимальным предельным коэффициентом, см. далее).
Направляющий столбец – столбец ведущего элемента, свободная неизвестная которого переводится в базисную (столбец с максимальной выгодой, см. далее).
Переменные x1, …, xm, входящие с единичными коэффициентами только в одно уравнение системы, с нулевыми – в остальные, называются базисными или зависимыми. В канонической системе каждому уравнению соответствует ровно одна базисная переменная. Переход осуществляется с помощью метода Гаусса–Жордана. Основная идея этого метода состоит в сведении системы m уравнений с n неизвестными к каноническому виду при помощи элементарных операций над строками.
Остальные n-m переменных (xm+1,…, xn) называются небазисными или независимыми переменными.
Базисное решение называется допустимым базисным решением, если значения входящих в него базисных переменных xj≥0, что эквивалентно условию неотрицательности bj≥0.
Допустимое базисное решение является угловой точкой допустимого множества S задачи линейного программирования и называется иногда опорным планом.
Если среди неотрицательных чисел bj есть равные нулю, то допустимое базисное решение называется вырожденным (вырожденной угловой точкой) и соответствующая задача линейного программирования называется вырожденной.
Пример №1 . Свести задачу линейного программирования к стандартной ЗЛП.
F(X) = x1 + 2x2 — 2x3 → min при ограничениях:
4x1 + 3x2 — x3≤10
— 2x2 + 5x3≥3
x1 + 2x3=9
Для приведения ЗЛП к канонической форме необходимо:
1. Поменять знак у целевой функции. Сведем задачу F(X) → min к задаче F(X) → max. Для этого умножаем F(X) на (-1). В первом неравенстве смысла (≤) вводим базисную переменную x4; во втором неравенстве смысла (≥) вводим базисную переменную x5 со знаком минус.
4x1 + 3x2-1x3 + 1x4 + 0x5 = 10
0x1-2x2 + 5x3 + 0x4-1x5 = 3
1x1 + 0x2 + 2x3 + 0x4 + 0x5 = 9
F(X) = — x1 — 2x2 + 2x3
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:
| 4 | 3 | -1 | 1 | 0 | 10 |
| 0 | -2 | 5 | 0 | -1 | 3 |
| 1 | 0 | 2 | 0 | 0 | 9 |
Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x4.
2. В качестве базовой переменной выбираем x2.
Разрешающий элемент РЭ=-2. Строка, соответствующая переменной x2, получена в результате деления всех элементов строки x2 на разрешающий элемент РЭ=-2. На месте разрешающего элемента получаем 1. В остальных клетках столбца x2 записываем нули. Все остальные элементы определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:
| 4-(0 • 3):-2 | 3-(-2 • 3):-2 | -1-(5 • 3):-2 | 1-(0 • 3):-2 | 0-(-1 • 3):-2 | 10-(3 • 3):-2 |
| 0 : -2 | -2 : -2 | 5 : -2 | 0 : -2 | -1 : -2 | 3 : -2 |
| 1-(0 • 0):-2 | 0-(-2 • 0):-2 | 2-(5 • 0):-2 | 0-(0 • 0):-2 | 0-(-1 • 0):-2 | 9-(3 • 0):-2 |
Получаем новую матрицу:
| 4 | 0 | 6 1 /2 | 1 | -1 1 /2 | 14 1 /2 |
| 0 | 1 | -2 1 /2 | 0 | 1 /2 | -1 1 /2 |
| 1 | 0 | 2 | 0 | 0 | 9 |
3. В качестве базовой переменной выбираем x3.
Разрешающий элемент РЭ=2. Строка, соответствующая переменной x3, получена в результате деления всех элементов строки x3 на разрешающий элемент РЭ=2. На месте разрешающего элемента получаем 1. В остальных клетках столбца x3 записываем нули. Все остальные элементы определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:
| 4-(1 • 6 1 /2):2 | 0-(0 • 6 1 /2):2 | 6 1 /2-(2 • 6 1 /2):2 | 1-(0 • 6 1 /2):2 | -1 1 /2-(0 • 6 1 /2):2 | 14 1 /2-(9 • 6 1 /2):2 |
| 0-(1 • -2 1 /2):2 | 1-(0 • -2 1 /2):2 | -2 1 /2-(2 • -2 1 /2):2 | 0-(0 • -2 1 /2):2 | 1 /2-(0 • -2 1 /2):2 | -1 1 /2-(9 • -2 1 /2):2 |
| 1 : 2 | 0 : 2 | 2 : 2 | 0 : 2 | 0 : 2 | 9 : 2 |
Получаем новую матрицу:
| 3 /4 | 0 | 0 | 1 | -1 1 /2 | -14 3 /4 |
| 1 1 /4 | 1 | 0 | 0 | 1 /2 | 9 3 /4 |
| 1 /2 | 0 | 1 | 0 | 0 | 4 1 /2 |
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (4,2,3).
Соответствующие уравнения имеют вид:
3 /4x1 + x4 — 1 1 /2x5 = -14 3 /4
1 1 /4x1 + x2 + 1 /2x5 = 9 3 /4
1 /2x1 + x3 = 4 1 /2
Выразим базисные переменные через остальные:
x4 = — 3 /4x1 + 1 1 /2x5-14 3 /4
x2 = — 1 1 /4x1 — 1 /2x5+9 3 /4
x3 = — 1 /2x1+4 1 /2
Подставим их в целевую функцию:
F(X) = — x1 — 2(- 1 1 /4x1 — 1 /2x5+9 3 /4) + 2(- 1 /2x1+4 1 /2)
или
F(X) = 1 /2x1 + x5-10 1 /2 → max
Система неравенств:
— 3 /4x1 + 1 1 /2x5-14 3 /4 ≥ 0
— 1 1 /4x1 — 1 /2x5+9 3 /4 ≥ 0
— 1 /2x1+4 1 /2 ≥ 0
Приводим систему неравенств к следующему виду:
3 /4x1 — 1 1 /2x5 ≤ -14 3 /4
1 1 /4x1 + 1 /2x5 ≤ 9 3 /4
1 /2x1 ≤ 4 1 /2
F(X) = 1 /2x1 + x5-10 1 /2 → max
Упростим систему.
3 /4x1 — 1 1 /2x2 ≤ -14 3 /4
1 1 /4x1 + 1 /2x2 ≤ 9 3 /4
1 /2x1 ≤ 4 1 /2
F(X) = 1 /2x1 + x2-10 1 /2 → max