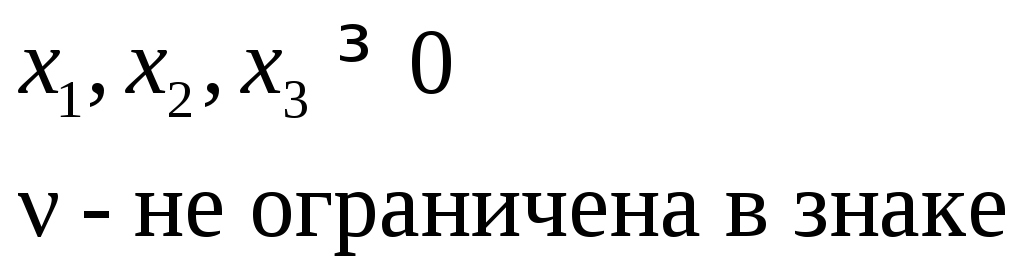- Пример решения матричной игры методом линейного программирования
- Второй способ нахождений двойственной задачи
- Решение матричной игры симплексным методом
- Решение матричной игры
- Алгоритм решения матричной игры
- Методы решения матричной игры в смешанных стратегиях
- 5.3.3 Решение матричных игр методами линейного программирования
- 5.3.3.1 Решение задачи лп симплекс-методом
Пример решения матричной игры методом линейного программирования
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.
Определим максимальное значение целевой функции F(X) = x1 + x2 + x3 при следующих условиях-ограничений.
6x1 + 5x2 + 7x3≤1
10x1 + 4x2 + 7x3≤1
13x1 + 10x2 + 4x3≤1
7x1 + 11x2 + 5x3=1
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
6x1 + 5x2 + 7x3 + 1x4 + 0x5 + 0x6 = 1
10x1 + 4x2 + 7x3 + 0x4 + 1x5 + 0x6 = 1
13x1 + 10x2 + 4x3 + 0x4 + 0x5 + 1x6 = 1
7x1 + 11x2 + 5x3 + 0x4 + 0x5 + 0x6 = 1
Введем искусственные переменные x.
6x1 + 5x2 + 7x3 + 1x4 + 0x5 + 0x6 + 0x7= 1
10x1 + 4x2 + 7x3 + 0x4 + 1x5 + 0x6 + 0x7= 1
13x1 + 10x2 + 4x3 + 0x4 + 0x5 + 1x6 + 0x7= 1
7x1 + 11x2 + 5x3 + 0x4 + 0x5 + 0x6 + 1x7= 1
Для постановки задачи на максимум целевую функцию запишем так:
F(X) = x1+x2+x3 — Mx7 => max
За использование искусственных переменных, вводимых в целевую функцию, накладывается так называемый штраф величиной М, очень большое положительное число, которое обычно не задается.
Полученный базис называется искусственным, а метод решения называется методом искусственного базиса.
Причем искусственные переменные не имеют отношения к содержанию поставленной задачи, однако они позволяют построить стартовую точку, а процесс оптимизации вынуждает эти переменные принимать нулевые значения и обеспечить допустимость оптимального решения.
Из уравнений выражаем искусственные переменные:
x7 = 1-7x1-11x2-5x3
которые подставим в целевую функцию:
F(X) = x1 + x2 + x3 — M(1-7x1-11x2-5x3) => max
или
F(X) = (1+7M)x1+(1+11M)x2+(1+5M)x3+(-1M) => max
Второй способ нахождений двойственной задачи
Используя последнюю итерацию прямой задачи найдем, оптимальный план двойственной задачи.
Из теоремы двойственности следует, что Y = C*A -1 .
Составим матрицу A из компонентов векторов, входящих в оптимальный базис.
Определив обратную матрицу А -1 через алгебраические дополнения, получим:
Как видно из последнего плана симплексной таблицы, обратная матрица A -1 расположена в столбцах дополнительных переменных .
Тогда
Решение матричной игры симплексным методом
Найти решение матричной игры. Решить матричные игры симплексным методом.
Задание. Свести задачу, заданную платежной матрицей, к задаче линейного программирования (предварительно упростив задачу, убрав строго доминируемые стратегии, если это возможно) и решить симплекс методом.
Решение проводим с помощью калькулятора.
| Игроки | B1 | B2 | B3 | a = min(Ai) |
| A1 | 0 | 3 | 1 | 0 |
| A2 | 3 | 0 | 5 | 0 |
| A3 | 2 | 1 | 1 | 1 |
| b = max(Bi ) | 3 | 3 | 5 | 0 |
Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(ai) = 1, которая указывает на максимальную чистую стратегию A3.
Верхняя цена игры b = min(bj) = 3.
Что свидетельствует об отсутствии седловой точки, так как a<>b, тогда цена игры находится в пределах 1
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
0x1 + 3x2 + 2x3-1x4 + 0x5 + 0x6 = 1
3x1 + 0x2 + 1x3 + 0x4-1x5 + 0x6 = 1
1x1 + 5x2 + 1x3 + 0x4 + 0x5-1x6 = 1
Поскольку задача решается на минимум и элементы единичной матрицы отрицательны, сведем задачу к нахождению максимума. Для этого умножим все строки на (-1) и будем искать первоначальный опорный план.
0x1-3x2-2x3 + 1x4 + 0x5 + 0x6 = -1
-3x1 + 0x2-1x3 + 0x4 + 1x5 + 0x6 = -1
-1x1-5x2-1x3 + 0x4 + 0x5 + 1x6 = -1
Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом.
Решим систему уравнений относительно базисных переменных: x4, x5, x6,
Полагая, что свободные переменные равны 0, получим первый опорный план: X1 = (0,0,0,-1,-1,-1)
| План | Базис | B | x1 | x2 | x3 | x4 | x5 | x6 |
| 0 | x4 | -1 | 0 | -3 | -2 | 1 | 0 | 0 |
| x5 | -1 | -3 | 0 | -1 | 0 | 1 | 0 | |
| x6 | -1 | -1 | -5 | -1 | 0 | 0 | 1 | |
| Индексная строка | F(X0) | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
Используя последнюю итерацию прямой задачи найдем, оптимальный план двойственной задачи.
Из теоремы двойственности следует, что Y = C*A -1 .
Составим матрицу A из компонентов векторов, входящих в оптимальный базис.
Определив обратную матрицу А -1 через алгебраические дополнения, получим:
Как видно из последнего плана симплексной таблицы, обратная матрица A -1 расположена в столбцах дополнительных переменных .
Тогда Y = C*A -1 =
Оптимальный план двойственной задачи равен:
y1 = 1 /3, y2 = 1 /3, y3 = 0
Z(Y) = 1* 1 /3+1* 1 /3+1*0 = 2 /3
Цена игры будет равна g = 1/F(x), а вероятности применения стратегий игроков:
pi = g*xi; qi = g*yi.
Цена игры: g = 1 : 2 /3 = 1 1 /2
Оптимальная стратегия игрока А: P( 1 /2 ; 1 /2; 0)
Оптимальная стратегия игрока B: Q( 1 /2; 1 /2; 0)
Пример №3 . Предприятие выпускает скоропортящуюся продукцию, которую сразу можно доставить потребителю (А1 стратегия). Отправить на склад для хранения (А2 стратегия) или подвергнуть обработке для длит. Хранения (А3 стратегия) . Потребитель может приобрести немедленно (В1 стратег) ,через некоторое время (В2 стратег) или после длительного периода (В3 стратегия).
В случае стратегий А2 и А3 предприятие несет дополнительные затраты на хранение и обработку продукции. Однако, при А2 следует вычесть убытки, если потребитель выберет стратегию В2 или В3 . Определить оптимальные пропорции для применения стратегий А1,А2,А3. Руководствуясь минимаксным критерием, гарантирует средний уровень убытка. Пользуясь минимальным критерием из таблицы.
| Игроки | B1 | B2 | B3 | a = min(Ai) |
| A1 | 2 | 3 | 2 | 2 |
| A2 | 4 | 2 | 1 | 1 |
| A3 | 1 | 3 | 3 | 1 |
| b = max(Bi ) | 4 | 3 | 3 | 0 |
Решение матричной игры находим через сервис решение матричной игры.
Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(ai) = 2, которая указывает на максимальную чистую стратегию A1.
Верхняя цена игры b = min(bj) = 3.
Что свидетельствует об отсутствии седловой точки, так как a<>b, тогда цена игры находится в пределах 2 Математические модели пары двойственных задач линейного программирования можно записать так:
найти минимум функции F(x) при ограничениях:
2x1+4x2+x3 >= 1
3x1+2x2+3x3 >= 1
2x1+x2+3x3 >= 1
F(x) = x1+x2+x3 = min
найти максимум функции Ф(y) при ограничениях:
2y1+3y2+2y3 4y1+2y2+y3 y1+3y2+3y3 Ф(y) = y1+y2+y3 = max
Решаем эти системы симплекс-методом.
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.
Определим минимальное значение целевой функции F(X) = x1 + x2 + x3 при следующих условиях-ограничений.
2x1 + 4x2 + x3≥1
3x1 + 2x2 + 3x3≥1
2x1 + x2 + 3x3≥1
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
2x1 + 4x2 + 1x3-1x4 + 0x5 + 0x6 = 1
3x1 + 2x2 + 3x3 + 0x4-1x5 + 0x6 = 1
2x1 + 1x2 + 3x3 + 0x4 + 0x5-1x6 = 1
Поскольку задача решается на минимум и элементы единичной матрицы отрицательны, сведем задачу к нахождению максимума. Для этого умножим все строки на (-1) и будем искать первоначальный опорный план.
-2x1-4x2-1x3 + 1x4 + 0x5 + 0x6 = -1
-3x1-2x2-3x3 + 0x4 + 1x5 + 0x6 = -1
-2x1-1x2-3x3 + 0x4 + 0x5 + 1x6 = -1
Цена игры будет равна g = 1/F(x), а вероятности применения стратегий игроков: pi = g*xi; qi = g*yi.
Цена игры: g = 1 : 5 /11 = 2 1 /5
p1 = 2 1 /5•0 = 0
p2 = 2 1 /5• 2 /11 = 2 /5
p3 = 2 1 /5• 3 /11 = 3 /5
q1 = 2 1 /5• 2 /11 = 2 /5
q2 = 2 1 /5•0 = 0
q3 = 2 1 /5• 3 /11 = 3 /5
Оптимальная стратегия игрока А: P( 0; 2 /5; 3 /5)
Оптимальная стратегия игрока B: Q( 2 /5;0; 3 /5)
Решение матричной игры
Инструкция . Выберите размерность матрицы, нажмите Далее . В новом диалоговом окне выберите метод решения матричной игры. Пример заполнения. Результаты вычислений оформляются в отчете формата Word .
Алгоритм решения матричной игры
В таблице представлены варианты решения игры, заданной платежной матрицей А.
| Наличие седловой точки | Отсутствие седловой точки | |
| Тип стратегии | Чистая стратегия | Смешанная стратегия |
| Метод решения | Решение найдено | 1. Через систему уравнений. 2. Графический метод. 3. Использование симплекс-метода. |
- На основании анализа платёжной матрицы следует определить, существуют ли в ней доминируемые стратегии, и исключить их.
- Найти верхнюю и нижнюю цены игры и определить, имеет ли данная игра седловую точку (нижняя цена игры должна быть равна верхней цене игры).
- Если седловая точка существует, то оптимальными стратегиями игроков, являющимися решением игры, будут их чистые стратегии, соответствующие седловой точке. Цена игры равна верхней и нижней цены игры, которые равны между собой.
- Если игра не имеет седловой точки, то решение игры следует искать в смешанных стратегиях. Для определения оптимальных смешанных стратегий в играх m × n следует использовать симплекс-метод, предварительно переформулировав игровую задачу в задачу линейного программирования.
Методы решения матричной игры в смешанных стратегиях
- Решение игры через систему уравнений.
Если задана квадратная матрица nxn ( n=m ), то вектор вероятностей можно найти, решив систему уравнений. Этот метод используется не всегда и применим только в отдельных случаях (если матрица 2×2 , то решение игры получается практически всегда). Если в решении получаются отрицательные вероятности, то данную систему решают симплекс-методом. - Решение игры графическим методом.
В случаях, когда n=2 или m=2 , матричную игру можно решить графически. - Решение матричной игры симплекс-методом.
В этом случае матричная игра сводится к задаче линейного программирования.
5.3.3 Решение матричных игр методами линейного программирования
Представленные выше примеры решение игры со смешенными стратегиями наглядно иллюстрируют теоретические положения матричных игр и трудоемкость ручного счета даже при матрице 2х2. Для авоматизации расчетов можно использовать программные продукты , метод расчета в которых основан на решении системы линейных уравнений http://www.uchimatchast.ru/.
Любую конечную игру двух лиц с нулевой суммой можно представить в виде задачи линейного программирования. При этом возможно решение задачи как с чистыми так со смешенными стратегиями. В случае чистых стратегий вероятность одной из стратегий будет равна единице, а вероятность остальных стратегий ,естественно, равна нулю.
Оптимальные значения вероятностей стратегийигрока А могут быть определены путем решения следующей максиминной задачи.
Сформулируем задачу матричной игры. Две конкурирующие компании А и B выпускают продукцию. Для увеличения продаж товар поставляется в различных упаковках. Компания А использует картон А1, целлофан А2, пластмасс А3. Компания B использует такие же материалы для упаковки. Однако, при этом компании использовали различные виды оформления упаковок. В компании А зафиксировали увеличение/уменьшение притока покупателей в зависимости от упаковки товара и стратегии поведения конкурента B. Эти статистические данные представлены в таблице.
Решение задачи основано на получение наилучшего результата из наихудших для каждого игрока, который может быть получен определенной стратегии поведения. Из представленной таблицы следует, что данную задачу нельзя решить на основе чистых стратегий (седловой точки нет). Решение задачи находится между -2 и 2. В данном случае присутствуют смешенные стратегии, а так как количество стратегий у игрока А равно трем эту задачу можно решить с помощью линейного программирования (ЛП) алгебраическим методом. Следует заметить, что эту задачу нельзя решить графическим методом, так как количество стратегий у каждого игрока больше двух.
В соответствии с данными, представленными в таблице, задача ЛП для игрока А записывается следующим образом
максимизировать: (максимальное количество клиентов) при выполнении следующих ограничений:
5.3.3.1 Решение задачи лп симплекс-методом
Приведем систему ограничений к каноническому виду, для этого необходимо неравенства преобразовать в равенства, с добавлением дополнительных переменных. Если в преобразуемом неравенстве стоит знак ≥, то при переходе к равенству знаки всех его коэффициентов и свободных членов меняются на противоположные. Тогда система запишется в виде:
Переходим к формированию исходной симплекс таблицы. В строку F таблицы заносятся коэффициенты целевой функции. Так как нам необходимо найти максимум целевой функции, то в таблицу заносятся коэффициенты с противоположным знаком
Так как среди исходного набора условий были равенства, мы ввели искусственные переменные R. Это значит, что в симплекс таблицу нам необходимо добавить дополнительную строку M, элементы которой рассчитываются как сумма соответствующих элементов условий-равенств (тех которые после приведения к каноническому виду содержат искусственные переменные R) взятая с противоположным знаком.
Из данных задачи составляем исходную симплекс таблицу.