Python угол между векторами numpy

Угол Numpy Объяснен Примерами

Функция NumPy angle() очень удобна и помогает нам добиться желаемого результата. Мы будем развивать более ясное представление об этом по мере продвижения вперед в этой статье.

Угол Numpy Объяснен Примерами

Привет гики и добро пожаловать в этой статье мы рассмотрим NumPy angle(). Наряду с этим, для общего лучшего понимания, мы также рассмотрим его синтаксис и параметр. Затем мы увидим применение всей теоретической части на нескольких примерах. Но сначала попробуем получить краткое представление о функции через ее определение.

Предположим, вы хотите выяснить угол сложного аргумента. Тогда, в этом случае, функция NumPy angle() пригодится и поможет нам достичь нашего результата. Мы будем развивать более ясное представление об этом по мере продвижения вперед в этой статье. В следующем разделе мы рассмотрим синтаксис, связанный с ним.

Синтаксис

numpy.angle(z,)

Это общий синтаксис нашей функции. В следующем разделе мы обсудим параметры и возвращаемое значение, связанные с ним.

ПАРАМЕТР

Этот параметр представляет собой комплексный аргумент или комплексное число, соответствующее которому должен быть вычислен угол.

Это необязательный параметр. По умолчанию он установлен в значение “false”, в этом случае он возвращает угол в радианах. В случае, если вы установите его в “true”, мы получим угол в градусах.

Возвращать

углы: ndarray или скалярные

Он возвращает угол против часовой стрелки от положительной вещественной оси по завершении программы.

Примеры, охватывающие Угол Numpy

Мы рассмотрели всю необходимую теорию, связанную с нашей функцией. Кроме того, мы рассмотрели его определение и разработали краткое понимание нашей функции. В этом разделе мы рассмотрим различные примеры, которые помогут нам лучше понять нашу функцию. Мы начнем с примера элементарного уровня и постепенно перейдем к более сложным примерам.

#input import numpy as ppool))

В приведенном выше примере сначала мы импортировали модуль NumPy. Затем использовали наш синтаксис для получения желаемого результата. Здесь мы указали степень истинности, благодаря которой получаем результат в градусах. Здесь результат оправдывает наш вклад. Мы можем понять это следующим образом. Мы рассмотрели (1+1j) как наше комплексное число. Здесь(вещественная часть) и(сложная часть). Тогда мы также знаем, что/a в этом случае. Что касается нашего состояния, то у нас есть степень. Следовательно, оправдано.

Мы также можем использовать эту функцию для массива чисел. Мы увидим это в следующем примере.

#input import numpy as ppool a=[1+2j,1,1j,3+4j]))

[63.43494882 0. 90. 53.13010235]

В этом примере мы выполнили все шаги, аналогичные первому. Но здесь вместо одного значения мы использовали массив. Результат во всех случаях оправдывает наш вклад, и поэтому мы можем сказать, что он верифицирован. Если хотите, можете перепроверить, как я сделал в первом примере.

Почему бы вам не попробовать комплексные числа по вашему выбору и не сказать мне, какой результат вы получили.

Ограничения угла Numpy

Функция NumPy angle-это действительно хорошая функция. Но у него тоже есть свои ограничения. Согласно определению, это помогает нам только в вычислении угла между сложными аргументами. Это означает, что мы не можем использовать эту функцию для вычисления значения угла между 2 точками или векторами. Он отлично работает в своей области, но за ее пределами от него нет большой пользы.

Что такое вектор и как вычислить угол между двумя векторами с помощью функции numpy angle

Векторы обычно определяются как физические величины, которые наряду с величиной имеют направление, связанное с ними. Элементарными примерами вектора являются перемещение, скорость и т. д. Векторы обычно представляются с помощью символического представления типа î(вдоль оси x), ĵ (вдоль оси y), k(вдоль оси z).

Теперь давайте попробуем выяснить, как вычислить угол между 2 векторами. Общая формула для расчета угла между ними такова

[COS (θ)= a.b/|a|.|b|] (consider an arrow symbol over a and b)

import numpy as np vec1 = [2, 1] vec2 = [1, 3] / np.linalg.norm(vec1) / np.linalg.norm(vec2).dot(unit1, unit2) print(np.arccos(dot_product))

В этом примере мы сначала импортировали модуль NumPy. Затем мы определили 2 наших массива, между которыми мы хотим вычислить угол. Затем мы использовали другую функцию библиотеки NumPy, которая называется linalg norm(). Эта функция возвращает одну из бесконечного числа векторных норм. Затем мы использовали функцию arccos, которая помогает нам вычислить значение href=”https://en.wikipedia.org/?title=Cosine&redirect=no”>cos обратный. Затем вычисляется наша стоимость. href=”https://en.wikipedia.org/?title=Cosine&redirect=no”>cos обратный. Затем вычисляется наша стоимость.

Обязательно Прочтите

• Вектор Python С Различными Операциями С Использованием Numpy
• Numpy Dot Product в Python С примерами
• Реализация Ханойской башни на Python

Вывод

В этой статье мы рассмотрели NumPy angle(). Кроме того, мы также рассмотрели его синтаксис и параметры. Для лучшего понимания мы рассмотрели несколько примеров. Мы варьировали синтаксис и рассматривали выходные данные для каждого случая. В конце концов, мы можем сделать вывод, что NumPy angle() используется для поиска угла для сложного аргумента. Надеюсь, эта статья смогла развеять все сомнения. Но если у вас есть какие-либо нерешенные вопросы, не стесняйтесь писать их ниже в разделе комментариев. Прочитав это, почему бы не прочитать дальше “Дельту Кронекера”?

Читайте ещё по теме:

Источник

Векторы и матрицы

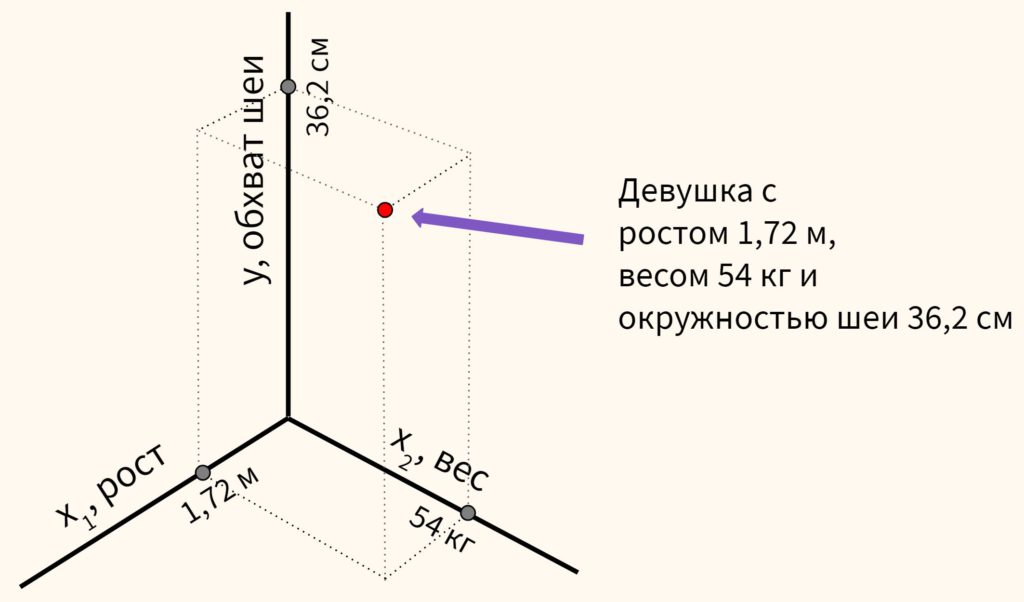
На самом деле измерений может быть и больше, просто так как мы живём в трёхмерном пространстве, представить четыре и более измерений мы не можем. Математически же это вполне возможно.

Данные как векторы и матрицы

Помимо того, что мы можем представить данные на графике (по крайней мере вплоть до третьего измерения), мы также можем представить их в форме вектора. Вектор, по сути, это набор чисел, описывающих координаты наших данных.

Если взять несколько точек и соответственно несколько векторов,

то получится набор чисел, называемых матрицей.

Из сказанного выше очевидно, что любой вектор — не что иное как матрица, в которой один столбец или одна строка.

Область математики, изучающая векторы и матрицы, называется линейной алгеброй.

На этом занятии мы рассмотрим два аспекта векторных и матричных вычислений. Во-первых, посмотрим на удобный способ умножения одного вектора на другой. Во-вторых, посмотрим как мы можем рассчитать угол между двумя векторами.

Умножение векторов

Вспомним, как мы делали прогноз с помощью нашей модели. Мы умножали вес (наклон) на значение независимой переменной и прибавляли ошибку (сдвиг). Когда у нас несколько независимых переменных и несколько весов, нам нужно их попарно перемножить и сложить произведения.

Если представить и веса, и значения независимых переменных с помощью векторов, то можно воспользоваться инструментом, который называется скалярным произведением векторов (dot product), чтобы получить прогнозное

Работа над ошибками. На видео представлена иная схема расположения векторов (см. скриншот ниже), а именно вектор-столбец весов мы умножаем на вектор-строку данных.

Результат вычислений от этого не меняется, однако исправленное положение векторов математически более точное.

Как мы узнаем на следующем курсе, перемножать можно не только векторы, но и матрицы. При этом при нахождении произведения двух матриц мы умножаем строки первой матрицы на столбцы второй. И здесь положение множителей будет иметь значение для вычисления конечного результата.

Поэтому и векторы, которые являются частным случаем матрицы с одной строкой или одним столбцом, правильнее расположить именно таким образом.

Добавлю, что если вы не вполне поняли, что это значит, ничего страшного, на следующем курсе мы во всем разберемся.

Скалярное произведение векторов на Питоне

На Питоне это реализовано с помощью библиотеки Numpy. До сих пор мы создавали массивы Numpy в, скажем так, служебных целях, чтобы использовать их, например, в моделях Scikit-learn.

Сегодня рассмотрим эти массивы сами по себе. По сути, массив Numpy (Numpy array), это и есть вектор или матрица. Давайте посмотрим, как создать такой массив, и как перемножить два вектора.

Вначале разберемся с основами работы с массивами.

Источник

Angles between two n-dimensional vectors in Python

In mathematics, a vector is a quantity that cannot be represented only by a single unit. It has to be divided into 2 components, namely magnitude and direction. Geometrically, a vector can be represented by a line segment with an arrow attached at its end. the arrow points at the direction of the vector.

Vectors can be implemented in python in the form of arrays. The arrays can be assigned like normal arrays or as numpy arrays. Numpy arrays can be n-dimensional.

Some properties of vectors

• When a vector is transmitted parallel to itself, it remains unchanged.
• Parallel vectors have the same direction.
• Vectors are said to be equal when they have the same magnitude and the direction.
• Vectors are said to be negative when they are equal in magnitude but opposite in direction.

In vector algebra we can calculate the angle between two vectors using a simple formula. The dot product of the two vectors can be used to determine the cosine of the angle between the two vectors which will ultimately give us our angle.

Let the two vectors be ‘u‘ and ‘v‘ and the angle between them be ‘A’ . The formula is given below:

The numerator represents the dot product of the two vectors whereas the denominator is the multiplication of the magnitudes of the two vectors.

Using python to determine the angle between two vectors

We can use Python to compute the angle between two vectors using user-defined functions or by using functions from the numerical python( Numpy) library. The numpy library contains functions such as linalg.norm() and arccos() that makes calculations easier. to know more about numpy, click here.

Implementing python functions for determining angles

We will be using the math library first and implement the function. The code for the program is as follows:

#importing required math module import math #calculating the magnitude of the vectors def mag(u, N): # Stores the final magnitude magnitude = 0 # Traverse the array for i in range(N): magnitude += u[i] * u[i] # Return the square root of magnitude return math.sqrt(magnitude) # Function to find the dot product of the vectors def dotProd(u, v, N): # Stores the dot product prod = 0 # Traverse the array for i in range(N): prod = prod + u[i] * v[i] # Return the product return prod def angleVector(u, v, N): # Stores the dot product of vectors dotProductOfVectors = dotProd(u, v, N) # magnitude of vector u magOfu = mag(u, N) #magnitude of vector v magOfv = mag(v, N) # angle between given vectors angle = (dotProductOfVectors / (magOfu * magOfv)) #display the angle print('%.5f'%angle) #pre defined vectors u = [-0.5, -2, 1] v = [-1, -1, 0.3] # Size of the vectors N = len(u) #display the angle print("The angle between the two vectors:") #function call to calculate the angle between the vectors angleVector(u, v, N)

The output of the above code will be the following:

The angle between the two vectors: 0.84529

Using numpy to calculate the angle between two n-dimensional vectors

Now let’s look at how we can easily calculate the angle using numpy.

#importing the required modules from numpy import arccos, array from numpy.linalg import norm import math #function for calculating the angle using numpy def angles(u, v): #using the arccos function from numpy return arccos(u.dot(v)/(norm(u)*norm(v))) #defining the vectors u = array([3, -4, 5]) v = array([2, 7, -3]) #function call to compute the angle c= angles(u,v) #the function returns the angle in radians #converting the angle to degrees from radians angle= math.degrees(c) #displaying the result print("the vectors are=",u,"and",v) print("the angle between the two vectors is=",angle)

The output of the above code will look like something as follows:

the vectors are= [ 3 -4 5] and [ 2 7 -3] the angle between the two vectors is= 131.647015792716

Summary.

This tutorial explores the various ways in which one can calculate the angle between two n dimensional vectors in python. The two programs shown in this article, demonstrates the usage of the math and the numpy libraries for the same. Using the dot product of the two given vectors and by calculating their individual magnitudes, the cosine of the angle can be determined and is used to define the relationship between them.

Источник