Python равномерное распределение случайных чисел

numpy.random.uniform

Выборки равномерно распределены по полуоткрытому интервалу [low, high) (включает низкий, но исключает высокий). Другими словами, любое значение в пределах данного интервала с равной вероятностью будет нарисовано uniform .

Вместо этого в новом коде следует использовать uniform метод экземпляра default_rng() ; см. Быстрый старт .

Нижняя граница выходного интервала.Все генерируемые значения будут больше или равны низкому.Значение по умолчанию равно 0.

high float или array_like чисел с плавающей запятой

Верхняя граница выходного интервала. Все сгенерированные значения будут меньше или равны high. Верхний предел может быть включен в возвращаемый массив чисел с плавающей запятой из-за округления с плавающей запятой в уравнении low + (high-low) * random_sample() . Значение по умолчанию — 1,0.

size int или кортеж целых чисел, необязательно

Форма вывода. Если заданная форма, например, (m, n, k) , то отрисовывается m * n * k выборок. Если размер равен None (по умолчанию), возвращается одно значение, если оба значения low и high являются скалярами. В противном случае np.broadcast(low, high).size образцы np.broadcast (low, high) .size .

Returns вне ndarray или скаляр

Нарисуйте образцы из параметризованного равномерного распределения.

Дискретное равномерное распределение,дающее целые числа.

Дискретное равномерное распределение по замкнутому интервалу [low, high] .

Поплавки равномерно распределены на [0, 1) .

Функция удобства, которая принимает размеры в качестве входных данных, например rand(2,2) будет генерировать массив чисел с плавающей запятой 2 на 2, равномерно распределенных по [0, 1) .

который следует использовать для нового кода.

Notes

Функция плотности вероятности равномерного распределения

в любом месте интервала [a, b) и ноль в другом месте.

>>> x = np.float32(5*0.99999999) >>> x 5.0

Examples

Нарисуйте образцы из распределения:

Все значения находятся в пределах заданного интервала:

>>> np.all(s >= -1) True >>> np.all(s < 0) True 

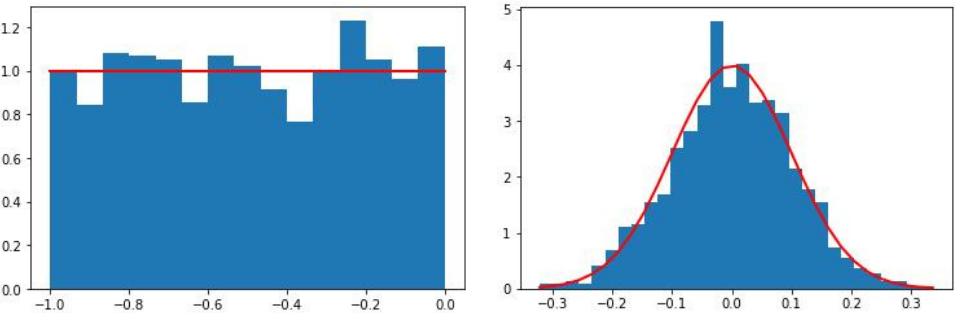
Отображение гистограммы образцов вместе с функцией плотности вероятности:

>>> import matplotlib.pyplot as plt >>> count, bins, ignored = plt.hist(s, 15, density=True) >>> plt.plot(bins, np.ones_like(bins), linewidth=2, color='r') >>> plt.show() 

Источник

numpy.random.uniform#

Samples are uniformly distributed over the half-open interval [low, high) (includes low, but excludes high). In other words, any value within the given interval is equally likely to be drawn by uniform .

New code should use the uniform method of a Generator instance instead; please see the Quick Start .

Lower boundary of the output interval. All values generated will be greater than or equal to low. The default value is 0.

high float or array_like of floats

Upper boundary of the output interval. All values generated will be less than or equal to high. The high limit may be included in the returned array of floats due to floating-point rounding in the equation low + (high-low) * random_sample() . The default value is 1.0.

size int or tuple of ints, optional

Output shape. If the given shape is, e.g., (m, n, k) , then m * n * k samples are drawn. If size is None (default), a single value is returned if low and high are both scalars. Otherwise, np.broadcast(low, high).size samples are drawn.

Returns : out ndarray or scalar

Drawn samples from the parameterized uniform distribution.

Discrete uniform distribution, yielding integers.

Discrete uniform distribution over the closed interval [low, high] .

Floats uniformly distributed over [0, 1) .

Convenience function that accepts dimensions as input, e.g., rand(2,2) would generate a 2-by-2 array of floats, uniformly distributed over [0, 1) .

which should be used for new code.

The probability density function of the uniform distribution is

anywhere within the interval [a, b) , and zero elsewhere.

>>> x = np.float32(5*0.99999999) >>> x 5.0 

Draw samples from the distribution:

All values are within the given interval:

>>> np.all(s >= -1) True >>> np.all(s  0) True 

Display the histogram of the samples, along with the probability density function:

>>> import matplotlib.pyplot as plt >>> count, bins, ignored = plt.hist(s, 15, density=True) >>> plt.plot(bins, np.ones_like(bins), linewidth=2, color='r') >>> plt.show() 

Источник

Готовимся к собеседованию: случайные числа в Python

Случайность управляет миром, а вы будете управлять случайностью. С помощью Python, конечно.

Кандидат философских наук, специалист по математическому моделированию. Пишет про Data Science, AI и программирование на Python.

Чтобы имитировать бросок кубика в игре или предсказать загруженность интернет-ресурса, нужны случайные числа.

Мы разобрали самые популярные вопросы о случайных числах в Python с собеседований. Чаще всего для ответа достаточно написать код и кратко его прокомментировать. Да пребудет с вами Великий Рандом!

Главное, что нужно помнить

• Случайные числа — это последовательность чисел, которая подчиняется одному из законов распределения.
• Главных распределений два: равномерное, с графиком в виде горизонтальной линии, и нормальное, с графиком-колоколом (его ещё называют гауссианой).

• Основная Python-библиотека для генерации случайных чисел называется random.
• Большинство случайных чисел в программировании — не случайные, а псевдослучайные.

Вопрос 1. Что такое случайные числа?

Сложность: 1/3

Что нужно помнить: случайные числа — это математическое понятие, и их не следует путать с обыденными, произвольными числами. Случайное число в математике и программировании — это:

Другими словами, существует закон или правило, которое называется «функцией распределения» или просто «распределением». И это самое распределение «раздаёт» каждому числу из диапазона определённую вероятность выпадения.

В качестве диапазона значений математикам и программистам привычнее всего использовать диапазон действительных чисел от 0 до 1, но это могут быть и целые числа от 1 до 6, как в игральном кубике, или от 100 до 1 000 000 — и так далее. Главное, что и распределение, и диапазон известны заранее, а само число нет.

Итого: случайные числа — это искусственно полученная последовательность чисел из определённого диапазона, которая подчиняется одному из законов распределения случайной величины.

Распределения бывают разные. Так, равномерное распределение — это когда любое значение из диапазона имеет одну и ту же вероятность выпадения (как у игрального кубика или монетки). Если же распределение, например, нормальное (гауссиана), то чаще выпадают числа из середины диапазона. Есть даже таблица — она поможет выбрать подходящее распределение.

Вопрос 2. Как получить случайные числа в Python?

Сложность: 1/3

Основных способов два: с помощью «родной» библиотеки random и с помощью модуля numpy.random из библиотеки numpy.

Прежде чем интервьюер придерётся, не забудьте сказать, что и random, и numpy.random — генераторы псевдослучайных чисел (о них ниже). Истинно случайные числа можно получить, например, c сайта Random.Org: там они генерируются с помощью атмосферного шума.

Наиболее популярный современный алгоритм генерирования псевдослучайных чисел разработан в 1997 году и носит красивое название «Вихрь Мерсенна». Он используется и в Python. Последовательность чисел, порождённая им, статистически неотличима от истинно случайной и имеет период, равный числу с шестью тысячами знаков. Этого хватает для задач симуляции и моделирования, но с точки зрения криптографии такая последовательность всё равно небезопасна: для успешной атаки достаточно иметь сравнительно небольшую сгенерированную этим генератором последовательность.

Вопрос 4. Как повторить случайную последовательность?

Сложность: 2/3

Истинно случайную последовательность повторить невозможно. Но для повторения псевдослучайных чисел в обеих основных библиотеках — random и numpy.random есть функция seed (), которая отвечает за инициализацию («посев») последовательности.

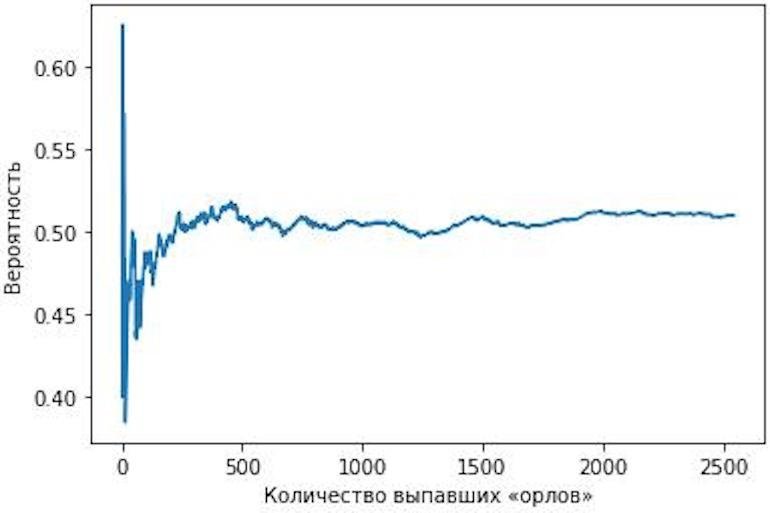
Чем больше бросков, тем ближе к 0,5 вероятность выпадения орла. Всё, как и предсказывает закон больших чисел.

Вопрос 8. Где применяются случайные числа?

Сложность: 2/3

В логистике: при расчётах страховых запасов товара — чтобы склад внезапно не опустел или, наоборот, не пришлось держать избыток товара слишком долго. Принято считать, что поведение покупателей случайно и подчиняется одной из разновидностей нормального распределения. В особо запущенных случаях считается случайным даже поведение поставщиков.

В науке: с помощью метода Монте-Карло учёные моделируют поведение частиц во фрактальном окружении в трёхмерном пространстве. Метод Монте-Карло основан на использовании большого количества генерируемых случайных чисел.

В микроэлектронике: броуновское движение частиц играет важную роль в формировании пористости плёночного покрытия полупроводников при напылении его на поверхность. Просчитать это на компьютере гораздо дешевле, чем экспериментировать с реальным покрытием, поэтому сначала его рассчитывают, а потом запускают в производство.

В криптографии: для генерации шифровальных ключей. Здесь становится особенно важным различие между псевдослучайными и истинно случайными числами.

Случайности не случайны

Так говорил мастер Угвэй, и мы теперь понимаем его чуть лучше: он жил довольно долго, мог заметить период повторения одних и тех же событий и догадаться, что все случайности в этом мире на самом деле псевдослучайны. У нас с вами времени меньше, поэтому придётся изучать документацию: random, numpy.random.

Читайте также:

Источник