Функции автозаполнения, создания матриц и числовых диапазонов
На предыдущем занятии мы познакомились с функцией array для создания произвольных массивов на основе переданного ей списка или кортежа. Однако, часто в инженерных задачах требуется определять векторы или матрицы с типовым набором значений, например, состоящих из нулей или единиц, или определение диагональной и единичной матриц и так далее. Конечно, мы можем все это сделать также через функцию array, используя механизм генерации списков, например, так:
np.array( [0]*10 ) # массив из 10 нулей np.array( [1]*15 ) # массив из 15 единиц np.array( [x for x in range(10)] ) # массив из чисел от 0 до 9
Но есть более быстрые способы (по скорости выполнения) создания подобных массивов. Для этого в NumPyимеются полезные функции, которые мы сейчас рассмотрим.
Функции автозаполнения элементов массива
Это только часть основных функций для создания массивов с заданными значениями. Использовать их достаточно просто. Например, так:
np.empty(10) # создание одномерного массива с произвольными числами np.empty(10, dtype='int16') np.empty((3, 2), dtype='float32') # возвращаетматрицу 3x2 стипомfloat32
Для функций eye и identity размерности указываются отдельными параметрами:
np.eye(4) # матрица 4х4 np.eye(4, 2) # матрица 4x2 np.identity(5) # матрица 5x5
Функции ones, zeros и full работают по аналогии с функцией empty:
np.zeros( (2, 3, 4) ) # нулевая матрица размерностью 2x3x4 np.ones( [4, 3], dtype='int8') # матрица 4x3 из единиц и типом int8 np.full((3, 2), -1) # матрица 3x2, состоящая из -1
Все эти функции работают быстрее, чем функция array с генератором списков языка Python. Поэтому их предпочтительно использовать при создании и инициализации массивов определенными значениями.
Функции создания матриц
Давайте посмотрим как работают эти функции.
np.mat('1 2 3 4') # создает матрицу 1x4 из строки np.mat('1, 2, 3, 4') # то же самое: создает матрицу 1x4 из строки np.mat('1 2; 3 4') # возвращает матрицу 2x2
Или же, вместо строк можно использовать список или кортеж:
Но, если из переданных данных нельзя сформировать прямоугольную таблицу (матрицу), то произойдет ошибка:
np.mat( [(1,2,3), (4,5,6,7)])# ошибка, размерности не совпадают
Следующая функция позволяет формировать диагональные матрицы:
np.diag([1, 2, 3]) # диагональная матрица 3x3
Но, если ей передать двумерный список, то она возвратит одномерный массив из элементов, стоящих на главной диагонали:
np.diag([(1,2,3), (4,5,6), (7,8,9)]) # выделение элементов главной диагонали
Если же мы хотим сформировать диагональную матрицу из многомерных списков или массивов, то следует воспользоваться функцией
Следующий набор функций используются для формирования треугольных матриц. Например:
np.tri(4) # треугольная матрица 4x4 np.tri(4, 2) # треугольная матрица 4x2
Если нужно привести уже существующие матрицы к треугольному виду, то это можно сделать так:
a = np.array( [(1,2,3), (4,5,6), (7,8,9)] ) np.tril(a) # нижняя треугольная матрица размером 3x3 np.triu(a) # верхняя треугольная матрица размером 3x3
Если указать одномерный список:
то будет создана треугольная матрица 3×3 из строк [1, 2, 3].
Также функции tril и triu будут работать и с многомерными массивами:
np.tril([[[1,2,3], [4,5,6], [7,8,9]]]) np.tril([[[1,2,3], [4,5,6], [7,8,9]], [[10,20,30], [40,50,60], [70,80,90]], [[100,200,300], [400,500,600], [700,800,900]]])
В этом случае последние двумерные сечения будут приведены к треугольному виду.
Последняя функция этойгруппы формирует матрицу Вандермонда из одномерных списков или массивов:
np.vander([1,2,3]) # матрица Вандермонда 3x3
Функции формирования числовых диапазонов
Следующая группа функций, которые мы рассмотрим на этом занятии, служит для формирования числовых диапазонов. Что делают эти функции? Когда мы с вами изучали язык Python, то говорили о функции
Давайте рассмотрим некоторые из них. Первая функция arrange довольно часто применяется в программах на Python. Она позволяет проходить заданный интервал с указанным шагом, например, так:
np.arange(5)# интервал [0; 5) с шагом 1 np.arange(1, 5)# интервал [1; 5) с шагом 1 np.arange(1, 5, 0.5) # интервал [1; 5) с шагом 0,5
Обратите внимание, в отличие от функции range языка Python в arrange пакета NumPy можно указывать вещественные значения. Вот еще один пример, демонстрирующий это:
Здесь все величины вещественные. Мы начинаем движение от значения 0 с шагом 0,1 пока не дойдем до значения пи (не включая его). И, далее, используя этот массив, можно вычислить синус или косинус от всех этих значений:
Видите, как это удобно. Без пакета NumPyнам пришлось бы писать цикл и делать вычисление для каждого значения аргумента. А здесь мы сразу получаем готовый массив значений функции косинуса. Это работает гораздо быстрее циклов в Python.
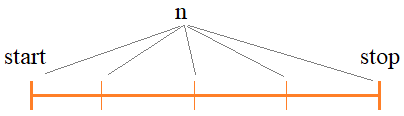
Похожим образом работает и функция linspace. Она разбивает указанный интервал на равномерные отрезки и возвращает массив этих значений:
Мы указываем в качестве аргументов интервал [start; stop] и число отметок в этом интервале n. Если n = 0, то получим пустой массив. При n = 1 – значение start. При n = 2 – значения start и stop. При n> 2 равномерное разбиение интервала точками m = n-2. Например:
np.linspace(0, np.pi, 0) # пустой массив np.linspace(0, np.pi, 1) # одно значение 0 np.linspace(0, np.pi, 2) # два значения: 0 и pi np.linspace(0, np.pi, 3) # три значения: 0, pi/2, pi
В чем отличие linspace от arange? В arange мы указываем сами шаг движения по числовой оси. При этом число значений определяется граничными значениями. А в linspace мы задаем граничные значения и число делений, а шаг вычисляется автоматически.
Функции logspace и geomspace работают аналогичным образом. У них указываются граничные значения и число членов, а на выходе имеем массив из соответствующих величин. Например:
np.logspace(0, 1, 3) # значения: 1, sqrt(10), 10 np.logspace(0, 1, 4) # значения: 1, 2.15, 4.64, 10 np.geomspace(1, 4, 3) # значения: 1, 2, 4 np.geomspace(1, 16, 5) # значения: 1, 2, 4, 8, 16
Остальные функции этой группы используются при построении графиков и мы их рассмотрим, когда будем рассматривать построение графиков с помощью библиотеки matplotlib.
Матрица из 0 и 1 где 1 стоят по краям
Вывести элементы, которые стоят по краям матрицы, сохраняя их положение в пространстве.
:Описать двумерный массив размерностью 7х7. Заполнить массив случайными значениями из диапазона от.
Найти все слова, в которых по краям стоят буквы ‘a’ и ‘b’, а между ними — не число.
В текстовое поле вводится строка текста типа "avb a1b a2b a3b a4b a5b abb acb ". При нажатии на.
Вывести лишь те элементы, которые стоят по краям матрицы, сохраняя их положение в пространстве
Описать двумерный массив размерностью 7х7. Заполнить массив случайными значениями из диапазона от.
Матрица, в которой по краям единицы, внутри двойки и тройки
Два дня уже сижу и пытаюсь понять логику этой матрицы. Как ее сделать? 1 1 1 1 1 1 1 2 2 2 2 1.
В бесплатном дизайне стоят баннеры, где их убрать?
Решил научиться на Joomla работать, вот скачал дизайн, но внизу баннеры, где они находяться, что бы.
m = int(input("Число сторок ")) n = int(input("Число столбцов ")) a = [[0] * m for _ in range(n)] for i in range(0, n): for j in range(0, m): a[i][0], a[i][-1] = 1, 1 a[0][j], a[-1][j] = 1, 1 for i in range(0, n): print(a[i], end="\t") print("\n")
import numpy as np m = int(input("Число сторок ")) n = int(input("Число столбцов ")) a = np.ones((m, n)) a[1:-1, 1:-1] = 0 print(a)