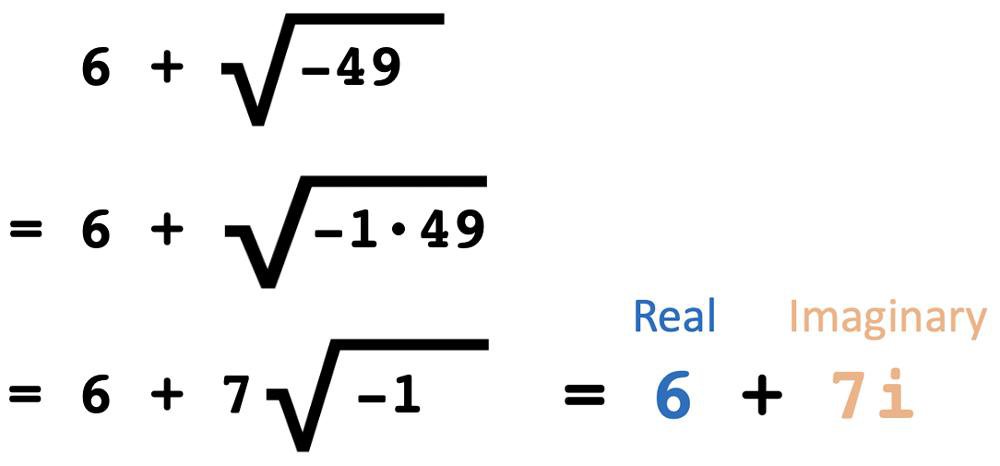Python complex numbers abs

Python Absolute Value – abs() for real and complex numbers

The absolute value of a number refers to that value’s magnitude, regardless of whether it is positive or negative. For example, the absolute value of -5 is 5.

Below is the syntax for using the abs() function to determine the absolute value of a number in Python:

Today we’ll look at some examples of where the abs() function could be applied, looking particularly at real and complex numbers.

Application 1: Integers and Floats

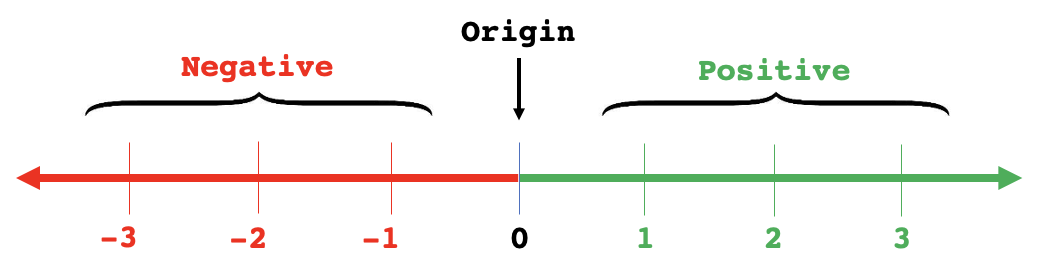
Applying the abs() function to a real number returns the magnitude of that number. We can define a real number as being on the real number line, represented in the image below. The magnitude of a real number refers to its distance along the line from the origin.

The sign of the number alludes to which direction along the line the number is; positive values are along the positive axis, and negative ones are along the negative axis. In the quick example shown in the introduction, -5 is a real number.

In regards to Python, real numbers are numbers that are integers or floats. The following example demonstrates how we can apply the abs function to a list of integers:

The use of the abs() function has converted the negative numbers into positive ones. For the positive numbers, there has been no change.

Remember that the absolute value of a real number refers to its distance from 0 and is known as magnitude. As magnitude is just a distance, it will always be positive.

We can also use the abs() function on floats. See below for an example of this:

Application 2: Complex Numbers

We can also apply the abs() function to complex numbers.

A complex number is a combination of real and imaginary numbers. We can define an imaginary number as being expressed in terms of the square root of a negative number. They are usually expressed in terms of the value $i$ or $j$, which means the square root of -1.

Imaginary numbers help fill a lot of gaps in mathematics. As a result, they are used quite commonly in maths-heavy industries, particularly in electrical engineering. The image below shows an example of a complex number:

The following code shows how you can create a complex number in Python and then apply the abs() function to get its magnitude:

In Python, we use j to represent the imaginary number because i is often used to represent indexes. For complex numbers, we use the Pythagorean theorem to calculate magnitude, like so:

$$\large \vert 6 + 7j \vert = \sqrt \approx 9.22$$

Summary

Getting the absolute value of a value in Python is quick and easy to do using the abs() function. The abs() function works with integers, floats, and complex numbers, so it should keep you covered in any situation where you may need to apply it.

Источник

cmath — Mathematical functions for complex numbers¶

This module provides access to mathematical functions for complex numbers. The functions in this module accept integers, floating-point numbers or complex numbers as arguments. They will also accept any Python object that has either a __complex__() or a __float__() method: these methods are used to convert the object to a complex or floating-point number, respectively, and the function is then applied to the result of the conversion.

For functions involving branch cuts, we have the problem of deciding how to define those functions on the cut itself. Following Kahan’s “Branch cuts for complex elementary functions” paper, as well as Annex G of C99 and later C standards, we use the sign of zero to distinguish one side of the branch cut from the other: for a branch cut along (a portion of) the real axis we look at the sign of the imaginary part, while for a branch cut along the imaginary axis we look at the sign of the real part.

For example, the cmath.sqrt() function has a branch cut along the negative real axis. An argument of complex(-2.0, -0.0) is treated as though it lies below the branch cut, and so gives a result on the negative imaginary axis:

>>> cmath.sqrt(complex(-2.0, -0.0)) -1.4142135623730951j 

But an argument of complex(-2.0, 0.0) is treated as though it lies above the branch cut:

>>> cmath.sqrt(complex(-2.0, 0.0)) 1.4142135623730951j 

Conversions to and from polar coordinates¶

A Python complex number z is stored internally using rectangular or Cartesian coordinates. It is completely determined by its real part z.real and its imaginary part z.imag . In other words:

Polar coordinates give an alternative way to represent a complex number. In polar coordinates, a complex number z is defined by the modulus r and the phase angle phi. The modulus r is the distance from z to the origin, while the phase phi is the counterclockwise angle, measured in radians, from the positive x-axis to the line segment that joins the origin to z.

The following functions can be used to convert from the native rectangular coordinates to polar coordinates and back.

Return the phase of x (also known as the argument of x), as a float. phase(x) is equivalent to math.atan2(x.imag, x.real) . The result lies in the range [-π, π], and the branch cut for this operation lies along the negative real axis. The sign of the result is the same as the sign of x.imag , even when x.imag is zero:

>>> phase(complex(-1.0, 0.0)) 3.141592653589793 >>> phase(complex(-1.0, -0.0)) -3.141592653589793 

The modulus (absolute value) of a complex number x can be computed using the built-in abs() function. There is no separate cmath module function for this operation.

Return the representation of x in polar coordinates. Returns a pair (r, phi) where r is the modulus of x and phi is the phase of x. polar(x) is equivalent to (abs(x), phase(x)) .

Return the complex number x with polar coordinates r and phi. Equivalent to r * (math.cos(phi) + math.sin(phi)*1j) .

Power and logarithmic functions¶

Return e raised to the power x, where e is the base of natural logarithms.

Returns the logarithm of x to the given base. If the base is not specified, returns the natural logarithm of x. There is one branch cut, from 0 along the negative real axis to -∞.

Return the base-10 logarithm of x. This has the same branch cut as log() .

Return the square root of x. This has the same branch cut as log() .

Trigonometric functions¶

Return the arc cosine of x. There are two branch cuts: One extends right from 1 along the real axis to ∞. The other extends left from -1 along the real axis to -∞.

Return the arc sine of x. This has the same branch cuts as acos() .

Return the arc tangent of x. There are two branch cuts: One extends from 1j along the imaginary axis to ∞j . The other extends from -1j along the imaginary axis to -∞j .

Hyperbolic functions¶

Return the inverse hyperbolic cosine of x. There is one branch cut, extending left from 1 along the real axis to -∞.

Return the inverse hyperbolic sine of x. There are two branch cuts: One extends from 1j along the imaginary axis to ∞j . The other extends from -1j along the imaginary axis to -∞j .

Return the inverse hyperbolic tangent of x. There are two branch cuts: One extends from 1 along the real axis to ∞ . The other extends from -1 along the real axis to -∞ .

Return the hyperbolic cosine of x.

Return the hyperbolic sine of x.

Return the hyperbolic tangent of x.

Classification functions¶

Return True if both the real and imaginary parts of x are finite, and False otherwise.

Return True if either the real or the imaginary part of x is an infinity, and False otherwise.

Return True if either the real or the imaginary part of x is a NaN, and False otherwise.

Return True if the values a and b are close to each other and False otherwise.

Whether or not two values are considered close is determined according to given absolute and relative tolerances.

rel_tol is the relative tolerance – it is the maximum allowed difference between a and b, relative to the larger absolute value of a or b. For example, to set a tolerance of 5%, pass rel_tol=0.05 . The default tolerance is 1e-09 , which assures that the two values are the same within about 9 decimal digits. rel_tol must be greater than zero.

abs_tol is the minimum absolute tolerance – useful for comparisons near zero. abs_tol must be at least zero.

The IEEE 754 special values of NaN , inf , and -inf will be handled according to IEEE rules. Specifically, NaN is not considered close to any other value, including NaN . inf and -inf are only considered close to themselves.

PEP 485 – A function for testing approximate equality

Constants¶

The mathematical constant π, as a float.

The mathematical constant e, as a float.

The mathematical constant τ, as a float.

Floating-point positive infinity. Equivalent to float(‘inf’) .

Complex number with zero real part and positive infinity imaginary part. Equivalent to complex(0.0, float(‘inf’)) .

A floating-point “not a number” (NaN) value. Equivalent to float(‘nan’) .

Complex number with zero real part and NaN imaginary part. Equivalent to complex(0.0, float(‘nan’)) .

Note that the selection of functions is similar, but not identical, to that in module math . The reason for having two modules is that some users aren’t interested in complex numbers, and perhaps don’t even know what they are. They would rather have math.sqrt(-1) raise an exception than return a complex number. Also note that the functions defined in cmath always return a complex number, even if the answer can be expressed as a real number (in which case the complex number has an imaginary part of zero).

A note on branch cuts: They are curves along which the given function fails to be continuous. They are a necessary feature of many complex functions. It is assumed that if you need to compute with complex functions, you will understand about branch cuts. Consult almost any (not too elementary) book on complex variables for enlightenment. For information of the proper choice of branch cuts for numerical purposes, a good reference should be the following:

Kahan, W: Branch cuts for complex elementary functions; or, Much ado about nothing’s sign bit. In Iserles, A., and Powell, M. (eds.), The state of the art in numerical analysis. Clarendon Press (1987) pp165–211.

Источник

Python abs() Function with examples

Python abs() Function returns the absolute (non-negative value) value of a number. For example, absolute value of -5 is 5 and absolute of 5 is also 5. In this guide, we will see how to use abs() function in Python with the help of examples.

Python abs() function works on?

The abs() function works on following numbers:
1. Integers, for example 6, -6, 1 etc.
2. Floating point numbers, for example 5.34, -1.44 etc
3. Complex numbers, for example 3+4j, 4+6j etc.

Python abs() example

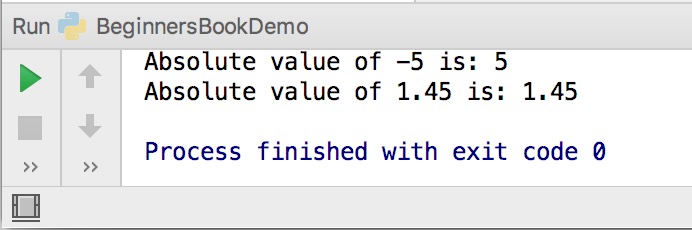
# integer number num = -5 print('Absolute value of -5 is:', abs(num)) # floating number fnum = -1.45 print('Absolute value of 1.45 is:', abs(fnum))

Output:

Python abs() function for complex numbers example

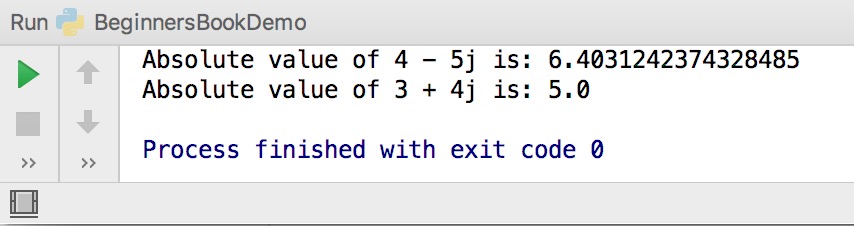
When a complex number is passed as an argument to abs() function, it returns the magnitude of the complex number. The magnitude of a complex number a + bj is equal to √a 2 +b 2 .

# complex number cnum = 4 - 5j print('Absolute value of 4 - 5j is:', abs(cnum)) cnum2 = 3 + 4j print('Absolute value of 3 + 4j is:', abs(cnum2))

Output:

Top Related Articles:

About the Author

I have 15 years of experience in the IT industry, working with renowned multinational corporations. Additionally, I have dedicated over a decade to teaching, allowing me to refine my skills in delivering information in a simple and easily understandable manner.

Источник