Программирование алгоритм построение алгоритма

Лекция 1. Основы построения алгоритмов и программирования

В данном разделе подробно описывается понятие алгоритма и программы, их свойства и принципы построения. Внимательно прочитав ее Вы не только узнаете, что такое алгоритм, но и научитесь создавать простейшие алгоритмы и программы.

Алгоритм

Итак, Вам поручено разработать алгоритм решения какой-либо задачи и Вы не знаете с чего начать? У Вас сразу возникает мысль позвонить по объявлению, чтобы Вашу контрольную работу сделал кто-нибудь другой?

Не спешите. Мы предлагаем Вам сначала разобраться, так ли это все сложно, что Вы не можете сделать это сами.

Представьте ситуацию. Вы много и тяжело работали и в конце концов заработали много денег, купили себе большой дом, наняли прислугу. Но вот беда: за много лет Вы так привыкли есть на завтрак бутерброды, а Ваш повар, как на зло, не умеет их готовить. Вы не можете отказаться от своей привычки (тем более, что имеете на нее полное право) и увольнять повара из-за такого пустяка Вам не хочется. Вполне логично, если Вы напишете ему инструкцию по приготовлению этого шедевра кулинарного искусства. Посмотрим, как могла бы выглядеть подобная инструкция:

Инструкция

по приготовлению бутербродов

1. Взять батон, масло, колбасу, сыр, немного зелени (салат, укроп, петрушку), кетчуп.
2. Отрезать небольшой ломтик от батона, тонкий ломтик от сыра и толстый кусок колбасы.
3. Намазать его маслом.
4. Положить ломтик сыра, затем лист салата (несколько веточек петрушки или укропа), и сверху кусок колбасы.
5. Повторить пункты 1-4 данной инструкции пока количество бутербродов не будет равно пяти.
6. Положить приготовленные бутерброды на сковороду и поставить на 5 минут в печь (духовку, тостер, гриль и т.д.).
7. Готовые бутерброды переложить на тарелку, полить кетчупом и подать к столу.

А теперь подумайте, смогли бы Вы составить такую инструкцию сами? Так ли это сложно для Вас? Неужели для Вас легче отказаться от привычки, чем написать подобную инструкцию? Если да — то можете не читать дальше, заплатить за выполнение контрольной работы n-ную сумму денег и забыть о том, что когда-нибудь Вы будете начальником (хорошим начальником в приличной фирме или организации). Итак, Вы составили подобную инструкцию и это не вызвало у Вас особых проблем. Приведенная инструкция и есть самый простой пример алгоритма. В повседневной жизни мы постоянно сталкиваемся с алгоритмами, поэтому само представление о том, что такое алгоритм, вряд ли является для Вас совершенно новым. Алгоритм решения задачи — это конечная последовательность четко сформулированных правил решения некоторого класса задач. Все люди постоянно сталкиваются с такими последовательностями — это и правила перехода улицы, и поиск нужного слова в словаре или книги в библиотеке, рецепты приготовления блюд и многое др. Все эти последовательности действий являются алгоритмами. Алгоритмы в математике — это правила нахождения корней квадратных алгебраических уравнений, правила выполнения арифметических действий, разложение числа на простые множители и др. Алгоритм обладает целым рядом свойств. Прежде всего — это дискретность, точность, понятность, а также результативность и массовость. Дискретность — это разбиение алгоритма на ряд отдельных законченных действий — шагов. Вернемся к нашей инструкции. Если не разбить ее на некоторое количество пунктов (шагов), то теряется сам смысл инструкции (алгоритма). Наша инструкция (алгоритм) как раз и нацелена на получение некоторого количества более простых и понятных последовательных действий. Отсюда следуют и другие свойства алгоритма. Точность — это указание последовательности шагов. Вызывает сомнение, что Вам понравился бы результат, если Ваш повар сначала положил продукты в печь, а затем начал бы нарезать. Понятность — это однозначное понимание и исполнение каждого шага алгоритма его исполнителем. Очевидно, что для успешного достижения результата, необходимо чтобы каждый пункт инструкции (алгоритма) был понятен его исполнителю (повару). Поэтому, прежде чем давать инструкции, необходимо выяснить, а какие команды будут поняты. Результативность — обязательное получение результата за конечное число шагов. Согласитесь, если бы Вы не были уверены, что в итоге получите именно те бутерброды, которые хотите, то и не начали бы составлять никакой инструкции. Массовость — применимость алгоритма к решению целого класса однотипных задач. Теперь, когда мы знаем, что такое алгоритм, как он выглядит и какими свойствами должен обладать, давайте попробуем вместе составить словесные алгоритмы решения некоторых задач. 1. 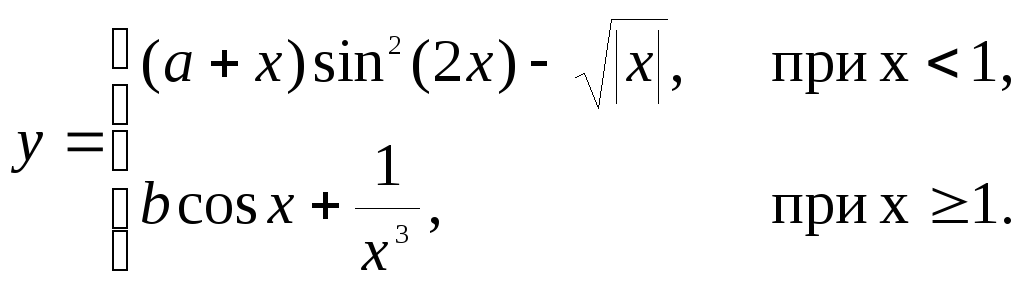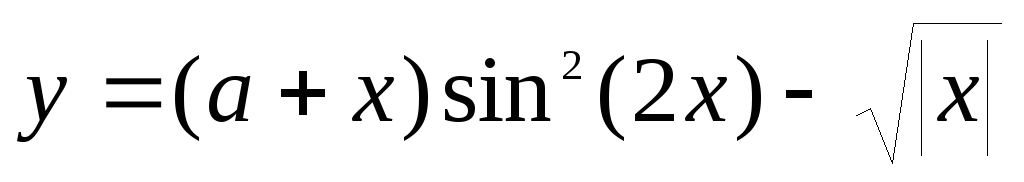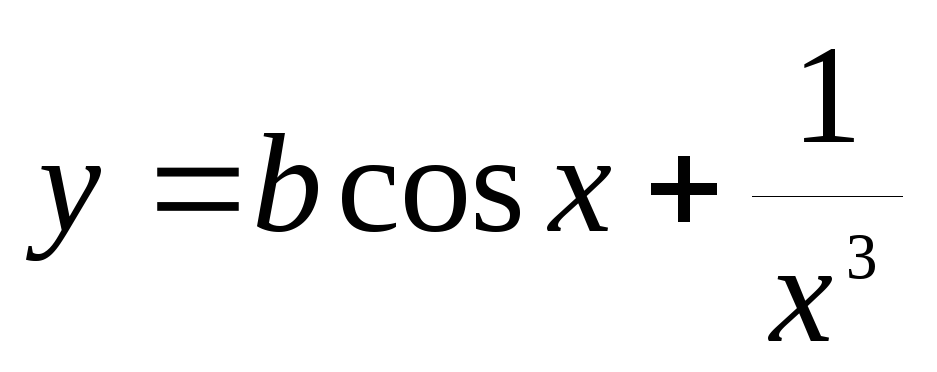Составить алгоритм вычисления следующей функции: a=2,68; b=1,75. х=1,27. Решение. Прежде, чем приступить к составлению алгоритма, давайте определим элементы функции и их назначение. Очевидно, в функции участвуют две формулы: и . Выбор, по какой из формул рассчитывать функцию, определяется значением переменной x. Числа a и b в формулах являются константами, введенными, во-первых, для более наглядного написания формул, а во-вторых, для расширения класса задач, решаемых данным алгоритмом (изменяя константы, мы получаем новые задачи). Итак, для того, чтобы получить решение, мы должны, во-первых, узнать, чему равны значения констант a и b, во-вторых, узнать, для какого значения х будем вычислять функцию, в-третьих, в зависимости от значения х выбрать формулу для расчета у и вычислить функцию, и, наконец, вывести (записать) полученный результат. Формально, алгоритм расчета функции будет выглядеть следующим образом:

1. Задаем значение a и b: a=2,68; b=1,75.
2. Получаем значение x, для которого надо вычислить функцию, х=1,27.
3. Если x
4. .
5. .

Записываем результат и завершаем работу.

2. Для функции вычислить значения для x[1,4], с шагом х=0,2; a=2,1, b=1,4. Решение. Определяем элементы функции и их назначение. Числа a и b являются константами, назначение которых то же, что и у констант в первом примере. х также является константой, смысл которой — задать шаг изменения значения переменной х. Для получения решения, мы должны, во-первых, узнать, чему равны значения констант a, b и х, во-вторых, задать начальное значение х, для которого будем вычислять функцию, в-третьих, производим расчет значения функции, записываем результат, увеличиваем х на значение х, если х4, то повторяем действия с расчетом функции, фиксированием результата и увеличением х, завершаем работу. Формально, алгоритм расчета функции будет выглядеть следующим образом:

1. Задаем значения констант a, b и х: a=2,1; b=1,4; х=0,2.
2. Задаем первое значение x: x=1.
3. Вычисляем значение функции для текущего значения х: .
4. Записываем результат.
5. Вычисляем следующее значение х: х=х+х.
6. Если х попадает в заданный интервал, то повторяем действия с пункта 3: если х4 — переходим к п.3.
7. Завершаем работу.

3. Дан массив из 5 чисел: Х=[2 4 6,2 3 1,4], вычислить значение функции 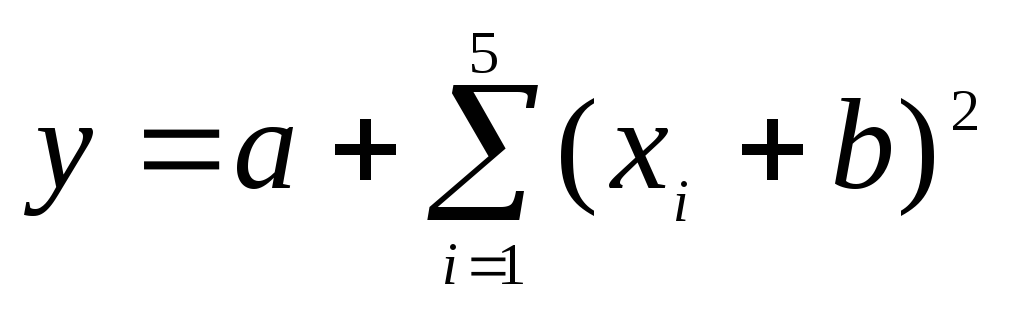, где a=27,8; b=4,24. Решение. Как и в предыдущих примерах, определяем элементы функции и их назначение. Числа a и b являются константами, назначение которых то же, что и у констант в первом примере. Появился новый элемент i — переменный индекс, указывающий какой элемент x_i нужно выбрать из массива Х. Для получения решения, нам необходимо, во-первых, узнать, чему равны значения констант a и b, во-вторых, просуммировать все элементы массива Х (предварительно добавив к каждому элементу константу b и возведя полученную сумму в квадрат), к полученному значению добавить константу a, записать результат вычислений и завершить вычисления. Остается добавить, что для того, чтобы просуммировать все элементы массива, мы должны сначала обнулить переменную, которая будет накапливать сумму (y), а затем по очереди (с помощью индекса i) выбираем элемент из массива, прибавляем к нему константу b, возводим в квадрат и добавляем к накапливающей переменной. Словесный алгоритм расчета функции:

1. Задаем значения констант a и b: a=27,8; b=4,24.
2. Вводим значения элементов массива Х.
3. Задаем начальные значения индекса i, и функции y: i=1, y=0.
4. Берем i-тый элемент массива Х, прибавляем к нему константу b, возводим полученную сумму в квадрат и прибавляем его к y: .
5. Проверяем, все ли элементы массива Х мы просуммировали (i должно быть равно 5) и если нет, то увеличиваем индекс i и возвращаемся к п.3: еслиii=i+1 и переход к п.3.
6. К накопленной сумме добавляем константу а: y=y+a.
7. Записываем результат.
8. Завершаем работу.

Мы рассмотрели три типа алгоритмов, которые потребуются Вам для решения контрольной работы. Естественно, что количество различных алгоритмов далеко не ограниченно. Более того, приведенные алгоритмы не являются жесткими конструкциями и Вы можете сами их менять по своему желанию или создать новые, результат выполнения которых будет точно таким же (например, в третьем задании суммировать элементы массива не в порядке возрастания, а в порядке убывания порядкового номера элемента и т.п.).

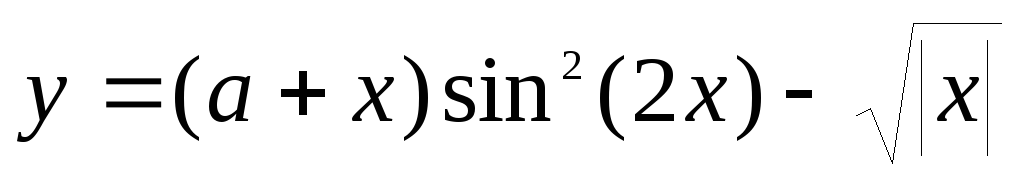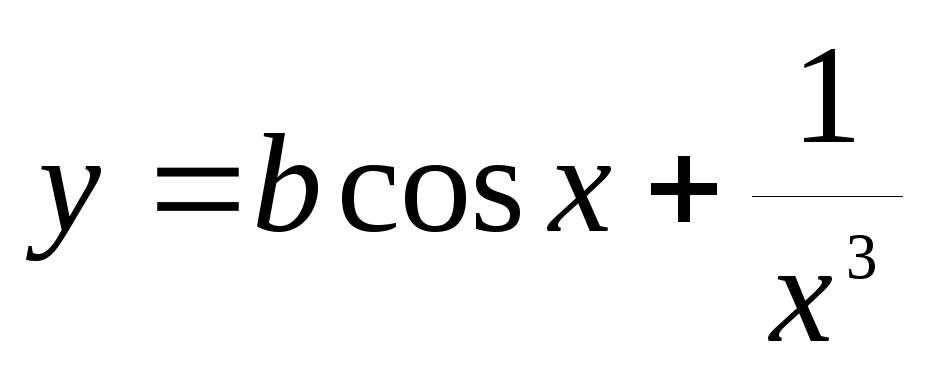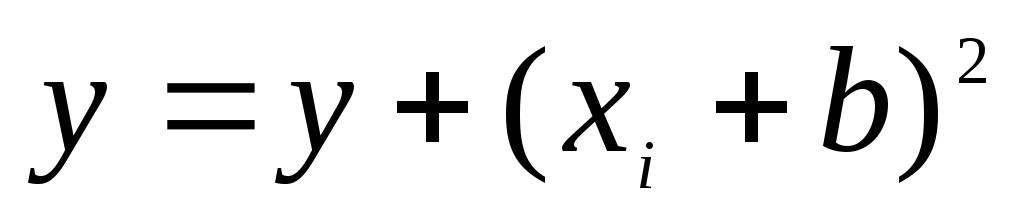Источник