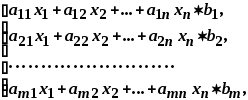Тест с ответами Линейное программирование
2. Экономико-математическая модель – это
а) математическое представление экономической системы (объектов, задачи, явлений, процессов и т. п.) +
б) качественный анализ и интуитивное представление объектов, задач, явлений, процессов экономической системы и ее параметров
в) эвристические описание экономической системы (объектов, задачи, явлений, процессов и т. п.)
3. Метод – это
а) подходы, пути и способы постановки и решения той или иной задачи в различных областях человеческой деятельности +
б) описание особенностей задачи (проблемы) и условий ее решения
в) требования к условиям решения той или иной задачи
4. Выберите неверное утверждение
а) ЭММ позволяют сделать вывод о поведении объекта в будущем
б) ЭММ позволяют управлять объектом +
в) ЭММ позволяют выявить оптимальный способ действия
г) ЭММ позволяют выявить и формально описать связи между переменными, которые характеризуют исследования
5. Экономико-математическая модель межотраслевого баланса – это
а) макроэкономическая, детерминированная, имитационная, матричная модель
б) микроэкономическая, детерминированная, балансовая, регрессионная модель
в) макроэкономическая, детерминированная, балансовая, матричная + модель
г) макроэкономическая, вероятностная, имитационная, матричная модель
6. Найти экстремум функции f(x) при выполнении ограничений Ri(x) = ai, φ (x) ≤ bj, наложенных на параметры функции – это задача
а) условной оптимизации +
б) линейного программирования
в) безусловной оптимизации
г) нелинейного программирования
д) динамического программирования
7. Задача, включающая целевую функцию f и функции Ф, входящие в ограничения, является задачей линейного программирования, если
а) все Ф и f являются линейными функциями относительно своих аргументов +
б) все Ф являются линейными функциями относительно своих аргументов, а функция f – нелинейна
в) функция f является линейной относительно своих аргументов, а функции Ф – нелинейны
г) только часть функций Ф и функция f являются линейными относительно своих аргументов
8. Множество всех допустимых решений системы задачи линейного программирования
а) является
б) выпуклым +
в) вогнутым
г) одновременно выпуклым и вогнутым
9. Если задача линейного программирования имеет оптимальное решение, то целевая функция достигает нужного экстремального значения в одной из:
а) вершин многоугольника (многогранника) допустимых решений +
б) внутренних точек многоугольника (многогранника) допустимых решений
в) точек многоугольника (многогранника) допустимых решений
10. В задачах линейного программирования решаемых симплекс-методом искомые переменные должны быть
а) Неотрицательными +
б) положительными
в) свободными от ограничений
г) любыми
11. Симплексный метод решения задач линейного программирования включает:
а) определение одного из допустимых базисных решений поставленной задачи (опорного плана)
б) определение правила перехода к не худшему решению
в) проверку оптимальности найденного решения
г) определение одного из допустимых базисных решений поставленной задачи (опорного плана), определение правила перехода к не худшему решению, проверка оптимальности найденного решения +
12. Задача линейного программирования не имеет конечного оптимума, если
а) в точке А области допустимых значений достигается максимум целевой функции F
б) в точке А области допустимых значений достигается минимум целевой функции F
в) система ограничений задачи несовместна
г) целевая функция не ограничена сверху на множестве допустимых решений +
14. Если ресурс образует «узкое место производства», то это означает
а) ресурс избыточен
б) ресурс использован полностью +
в) двойственная оценка ресурса равна нулю
15. Критерием остановки вычислений в алгоритме поиска оптимального решения методами одномерной оптимизации является условие
а) отношение длины текущего интервала неопределенности к длине первоначального интервала меньше заданной величины ε
б) значение целевой функции (ЦФ), вычисленное в текущей точке, меньше значения ЦФ, вычисленного в последующей точке
в) отношение длины текущего интервала неопределенности к длине первоначального интервала больше заданной величины ε
г) значение ЦФ, вычисленное в текущей точке, меньше значения ЦФ, вычисленного в предыдущей точке +
16. Если целевая функция и все ограничения выражаются с помощью линейных уравнений, то рассматриваемая задача является задачей
а) динамического программирования
б) линейного программирования +
в) целочисленного программирования
г) нелинейного программирования
17. Модель задачи линейного программирования, в которой целевая функция исследуется на максимум и система ограничений задачи является системой уравнений, называется
а) стандартной
б) канонической +
в) общей
г) основной
д) нормальной
18. Модель задачи линейного программирования, в которой целевая функция исследуется на максимум и система ограничений задачи является системой неравенств, называется
а) стандартной
б) канонической
в) общей +
г) основной
д) нормальной
19. В линейных оптимизационных моделях, решаемых с помощью геометрических построений число переменных должно быть
а) не больше двух +
б) равно двум
в) не меньше двух
г) не больше числа ограничений +2
д) сколько угодно
20. Задача линейного программирования может достигать максимального значения
а) только в одной точке
б) в двух точках
в) во множестве точек +
г) в одной или двух точках
д) в одной или во множестве точек
1. Если в прямой задаче, какое либо ограничение является неравенством, то в двойственной задаче соответствующая переменная
а) Неотрицательна +
б) положительна
в) свободна от ограничений
г) отрицательная
2. Транспортная задача является задачей …. Программирования
а) динамического
б) нелинейного
в) линейного +
г) целочисленного
д) параметрического
3. Если в транспортной задаче объем спроса равен объему предложения, то такая задача называется
а) замкнутой
б) закрытой +
в) сбалансированной
г) открытой
д) незамкнутой
4. Если в транспортной задаче объем запасов превышает объем потребностей, в рассмотрение вводят
а) фиктивный пункт производства
б) фиктивный пункт потребления +
в) изменения структуры не требуются
5. Методы теории игр предназначены для решения задач
а) с конфликтными ситуациями в условиях неопределенности +
б) с полностью детерминированными условиями
в) статистического моделирования
6. Стратегия игрока – это совокупность правил, определяющих выбор его действий при
а) каждом ходе в зависимости от сложившейся ситуации в одном сеансе игры +
б) одном ходе игры
в) всех сеансах игры
7. Нижняя цена игры – это
а) максимин, т.е. максимальный выигрыш по всем стратегиям одного из игроков среди минимальных значений выигрышей каждой его стратегии +
б) гарантированный выигрыш одного из игроков при любой стратегии другого игрока
в) минимакс, т.е. минимальный проигрыш по всем стратегиям одного из игроков среди максимальных значений проигрышей каждой его стратегии
8. Верхняя цена игры – это
а) минимакс, т.е. минимальный проигрыш по всем стратегиям одного из игроков среди максимальных значений проигрышей каждой его стратегии +
б) гарантированный проигрыш одного из игроков при любой стратегии другого игрока
в) максимин, т.е. максимальный выигрыш по всем стратегиям одного из игроков среди минимальных значений выигрышей каждой его стратегии
9. Решение игры в чистых стратегиях определяется
а) ценой игры, равной нижней цене игры
б) ценой игры, равной верхней цене игры
в) наличием седловой точки
г) всем перечисленным в ответах на это задание +
10. Решение игры в смешанных стратегиях определяется
а) вероятностью выбора каждой из активных (полезных) стратегий, совокупный выигрыш которых представляет случайную величину с математическим ожиданием равным цене игры +
б) ценой игры, равной нижней цене игры
в) ценой игры, равной верхней цене игры
г) наличием седловой точки
11. Задача, процесс нахождения решения которой является многоэтапным, относится к задачам
а) линейного программирования
б) теории игр
в) динамического программирования +
г) нелинейного программирования
д) параметрического программирования
12. Определите, что включает симплексный метод решения задач линейного программирования:
а) определение одного из допустимых базисных решений поставленной задачи (опорного плана)
б) определение правила перехода к не худшему решению
проверку оптимальности найденного решения
в) определение одного из допустимых базисных решений поставленной задачи (опорного плана), определение правила перехода к не худшему решению, проверка оптимальности найденного решения +
13. Выберите правильный вариант. Задача линейного программирования не имеет конечного оптимума, если:
а) в точке А области допустимых значений достигается максимум целевой функции F
б) в точке А области допустимых значений достигается минимум целевой функции F
в) система ограничений задачи несовместна
г) целевая функция не ограничена сверху на множестве допустимых решений +
14. Как называется модель задачи линейного программирования, в которой целевая функция исследуется на максимум и система ограничений задачи является системой уравнений?
а) стандартной
б) канонической +
в) общей
г) основной
д) нормальной
15. Что должно быть в линейных оптимизационных моделях, решаемых с помощью геометрических построений число переменных?
а) не больше двух +
б) равно двум
в) не меньше двух
г) не больше числа ограничений +2
д) сколько угодно
16. Отметьте, какое максимальное значение может достигать задача линейного программирования?
а) только в одной точке
б) в двух точках
в) во множестве точек +
г) в одной или двух точках
д) в одной или во множестве точек
17. Выберите верный вариант. Если в прямой задаче, какое либо ограничение является неравенством, то в двойственной задаче соответствующая переменная:
а) неотрицательна +
б) положительна
в) свободна от ограничений
г) отрицательная
18. Вставьте пропущенное слово. Транспортная задача является задачей ___________ программирования.
а) динамического
б) нелинейного
в) линейного +
г) целочисленного
д) параметрического
19. Как называется задача, если в транспортной задаче объем спроса равен объему предложения:
а) замкнутой
б) закрытой +
в) сбалансированной
г) открытой
д) незамкнутой
20. Выберите верный вариант. Если в транспортной задаче объем запасов превышает объем потребностей, в рассмотрение вводят:
а) фиктивный пункт производства
б) фиктивный пункт потребления +
в) изменения структуры не требуются
1)Задача линейного программирования и различные формы ее записи. Приведение общей задачи лп к симметричной форме записи.
Если целевая функция и система ограничений линейны, то задача математического программирования называется задачей линейного программирования (ЗЛП).
означает «» , «» или » /html/2706/294/html_1Zz9KUz02H.gabz/img-d2us4Z.png» name=»Рисунок 1″ align=»bottom» width=»298″ height=»37″ border=»0″>
Основная форма ЗЛП
Симметричная форма ЗЛП
Общая задача линейного программирования
Любая задача линейного программирования приводится к стандартной (канонической) форме основной задачи линейного программирования, которая формулируется следующим образом: найти неотрицательные значения переменных X1, X2, Xn, удовлетворяющих ограничениям в виде равенств:
A11X1 + A12X2 + … + A1nXn = B1;
A21X1 + A22X2 + … + A2nXn = B2;
Am1X1 + Am2X2 + … + AmnXn = Bm;
и обращающих в максимум линейную функцию этих переменных:
E = C1X1 + C2X2 + … + CnXn Þ max
При этом также требуется, чтобы правые части равенств были неотрицательны, т.е. должны соблюдаться условия:
Приведение к стандартной форме необходимо, так как большинство методов решения задач линейного программирования разработано именно для стандартной формы. Для приведения к стандартной форме задачи линейного программирования может потребоваться выполнить следующие действия:
перейти от минимизации целевой функции к ее максимизации;
изменить знаки правых частей ограничений;
перейти от ограничений-неравенств к равенствам;
избавиться от переменных, не имеющих ограничений на знак.
Для решения нашей задачи воспользуемся симплекс-методом, так как этот метод предназначен для решения задач линейного программирования любой размерности.
2)Приведение общей задачи лп к каноническому виду.
Любую задачу линейного программирования можно свести к задаче линейного программирования в канонической форме. Для этого в общем случае нужно уметь сводить задачу максимизации к задаче минимизации; переходить от ограничений неравенств к ограничениям равенств и заменять переменные, которые не подчиняются условию неотрицательности. Максимизация некоторой функции эквивалента минимизации той же функции, взятой с противоположным знаком, и наоборот.
Правило приведения задачи линейного программирования к каноническому виду состоит в следующем: