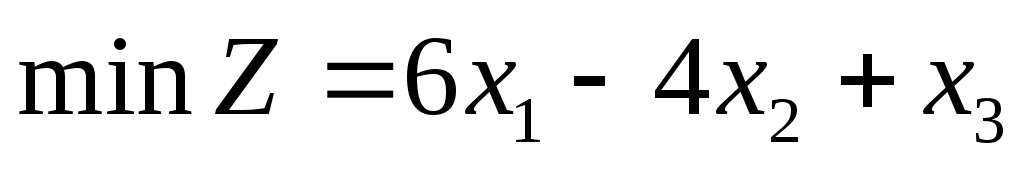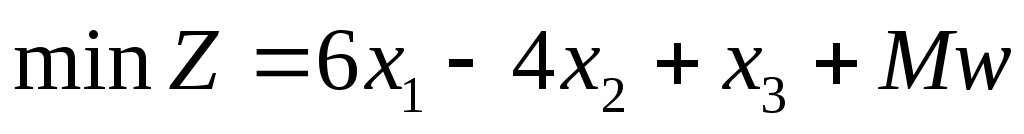Предпочтительный вид задачи линейного программирования

Указания к решению задач линейного программирования

Задачи линейного программирования были первыми, подробно изученными задачами поиска экстремума функций при наличии ограничений типа неравенств. Присутствие в названии термина «программирование» объясняется тем, что первые исследования и первые приложения линейных оптимизационных задач были в сфере экономики. В английском языке слово «programming» означает планирование, составление планов или программ. Вполне естественно, что терминология отражает тесную связь, существующую между математической постановкой задачи и её экономической интерпретацией (изучение оптимальной экономической программы). Термин «линейное программирование» был предложен Дж. Данцигом в 1949 г. для изучения теоретических и алгоритмических задач, связанных с оптимизацией линейных функций при линейных ограничениях.

Общей задачей линейного программирования (ЗЛП) называют задачу

и условие неотрицательности компонент

Здесь — заданные вещественные числа, функция называется целевой, вектор — план задачи. План, который удовлетворяет системе ограничений (1.2), называется допустимым. Допустимый план, при котором целевая функция достигает наибольшее или наименьшее значение, называется оптимальным. Возможны следующие случаи:

1. Оптимальный план единственный;

2. Оптимальных планов бесконечное множество;

3. Целевая функция неограниченна на множестве допустимых планов;

4. Область допустимых решений состоит из одной точки, где целевая функция достигает одновременно и наибольшее и наименьшее значения.

Пример 1. Рассмотрим следующую ЗЛП

Решим эту задачу графически. Для этого на плоскости построим декартову систему координат . Каждое из неравенств системы (1.3) задает на плоскости некоторую полуплоскость. Пересечение любого числа полуплоскостей есть выпуклое множество.

Напомним, что выпуклым называется такое множество, любые две точки которого можно соединить отрезком прямой, все точки которого принадлежат данному множеству. Примером выпуклого множества является треугольник.

Построим по двум точкам каждую из граничных прямых

Теперь в произвольной точке (например, в точке O (0,0)) определяем, какой знак неравенства выполняется и выбираем нужную полуплоскость. Пересечением выбранных полуплоскостей будет треугольник, множество точек этого треугольника есть допустимое множество решений ЗЛП (1.3). На рис.1 треугольник закрашен темным цветом.

Теперь построим линию уровня целевой функции

Из начала координат построим вектор-градиент ,

компонентами которого являются коэффициенты целевой функции. Данный вектор показывает направление наискорейшего роста функции. Для простоты на рисунке изображен вектор .

Будем двигать линию уровня в направлении градиента до пересечения с многогранником допустимых решений. Первая точка пересечения M будет точкой минимума. Координаты этой точки M (2,1) определяем из системы

Таким образом, оптимальный план ЗЛП (1.3) есть . Конец задачи.

Симметричной формой записи ЗЛП называется задача

В экономической теории задачи (1.4), (1.5) встречаются наиболее часто.

Наконец, канонической формой записи ЗЛП называют задачу

Система ограничений задачи (1.6) представляет собой линейную алгебраическую систему. В матричной форме ее можно записать так

Для того чтобы ЗЛП имела решение, ее система ограничений должна быть совместной. Это возможно, если ранг матрицы совпадает с рангом расширенной матрицы . Обозначим

Переменные ЗЛП, соответствующие векторам базиса, называются базисными и обозначаются БП. Остальные переменных будут свободными и обозначаются СП. Если свободные переменные приравнять нулю, а базисные переменные при этом примут неотрицательные значения, то полученное частное решение системы (1.7) называется опорным решением (планом).

Будем говорить, что система ограничений (1.7) ЗЛП имеет предпочтительный вид, если при неотрицательности правой части левая часть ограничения содержит переменную, входящую с коэффициентом, равным единице, а в остальные ограничения-равенства – с коэффициентом, равным нулю. Например, в системе ограничений

первое и второе ограничения имеют предпочтительный вид, а третье – нет.

В 1820 г. Ж.Фурье и затем в 1947 г. Дж. Данциг предложили метод направленного перебора смежных вершин в направлении возрастания целевой функции — симплекс-метод, ставший основным при решении задач линейного программирования. Советский академик, лауреат Нобелевской премии (1975 г.) Л.В. Канторович, сформулировал ряд задач линейного программирования и предложил (1939 г.) метод их решения (метод разрешающих множителей), незначительно отличающийся от симплекс-метода.

Метод решения ЗЛП, который называется симплексным, применяется лишь к канонической форме записи. Преобразуем симметричную форму записи ЗЛП к канонической. Пусть исходная задача имеет вид (1.4). Введем m дополнительных переменных Для того чтобы неравенства типа преобразовать в равенство, прибавим к левым частям дополнительные переменные. В целевую функцию эти переменные входят с нулевыми коэффициентами. Система ограничений в задаче (1.4) примет вид

Здесь — базисные переменные, — свободные. Следовательно, начальный опорный план примет вид .

Рассмотрим теперь задачу (1.5). Также введем m дополнительных переменных но для того, чтобы неравенства типа преобразовать в равенства, вычтем из левых частей дополнительные переменные. (В целевую функцию эти переменные войдут с нулевыми коэффициентами.)

Однако теперь система ограничений не имеет предпочтительный вид, так как дополнительные переменные входят в левую часть (при ) с коэффициентами, равными -1. Поэтому, базисный план

является недопустимым. В этом случае вводится искусственный базис . В целевую функцию переменные вводятся с коэффициентом , где — большое положительное число.

Полученная задача называется M-задачей, соответствующей исходной. Она всегда имеет предпочтительный вид. Ее начальный опорный план есть

Пусть исходная ЗЛП имеет вид

Причем ни одно из ограничений не имеет предпочтительной переменной. M -задача запишется так

где знак + в целевой функции относится к задаче на минимум. Начальный опорный план в этом случае будет

Если некоторые из системы ограничений имеют предпочтительный вид, то в них не следует вводить искусственные переменные.

Пример 2. Рассмотрим следующую ЗЛП

Приведем задачу к каноническому виду, для этого введем дополнительные переменные

Второе уравнение не содержит базисной переменной, поэтому добавим в этом уравнении искусственный базис . В результате получаем M -задачу

Предположим теперь, что ЗЛП имеет предпочтительный вид

Задачу (1.9) запишем в таблицу, которая называется симплексной

Последнюю строку в этой таблице называют индексной строкой. Число есть значение целевой функции. Числа называют оценками свободных переменных. Элементы последнего столбца называют симплексным отношением. Преобразование ЗЛП к новому базису назовем симплексными преобразованиями.

Пример 3. Составим симплексную таблицу для задачи (1.8) в примере 2

Здесь в первой строке стоят коэффициенты целевой функции при соответствующих переменных. В первом столбце стоят коэффициенты целевой функции при базисных переменных.

Приведем теперь основные теоремы симплексного метода.

Теорема 1. Пусть исходная задача решается на максимум. Если для некоторого опорного плана все оценки неотрицательны, то такой план оптимален.

Теорема 2. Пусть исходная задача решается на минимум и для некоторого опорного плана все оценки неположительны, то такой план оптимален.

Теорема 3. Если в индексной строке последней симплексной таблицы, содержащей оптимальный план, имеется хотя бы одна нулевая оценка, соответствующая свободной переменной, то ЗЛП имеет бесконечное множество оптимальных планов.

Теорема 4. Если в индексной строке симплексной таблицы ЗЛП на максимум содержится отрицательная оценка , а в соответствующем столбце переменной нет ни одного положительного элемента, то целевая функция на множестве допустимых планов не ограничена сверху.

Теорема 5. Если в индексной строке симплексной таблицы ЗЛП на минимум содержится положительная оценка , а в соответствующем столбце переменной нет ни одного положительного элемента, то целевая функция на множестве допустимых планов не ограничена снизу.

Теорема 6. Если в оптимальном плане M -задачи хотя бы одна из искусственных переменных отлична от нуля, то исходная задача не имеет допустимых планов, т.е. ее система ограничений несовместна.

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник

1.5. Симплексный метод решения задач линейного программирования

1. Привести ЗЛП к каноническому виду с неотрицательной правой частью.
2. Найти какой-либо начальный опорный план . Если опорный план отсутствует, то задача не имеет решения вследствие несовместности системы ограничений.
3. Проверить найденный план на оптимальность, используя оценки заполненной симплексной таблицы.
4. Если план оптимален, то задача решена.
5. Если план оптимален, но не единственен, то можно найти еще один оптимальный план.
6. Если план не оптимален, но имеет место условие неограниченности целевой функции, то задача не имеет решения.
7. Если пункты 4) – 6) алгоритма не выполняются, найти новый опорный план и перейти к пункту 3).

Нахождение начального опорного плана злп ( )

Пусть система ограничений ЗЛП представлена в канонической форме записи с неотрицательной правой частью. . Говорят, что ограничение ЗЛП имеет предпочтительный вид, если при неотрицательной правой части () левая часть ограничения содержит переменную, входящую с коэффициентом, равным единице, а в остальные ограничения-равенства – с коэффициентом, равным нулю. Например, в системе ограничений: первое и второе ограничения имеют предпочтительный вид, а третье – нет (предпочтительные переменные подчеркнуты). Если каждое ограничение системы имеет предпочтительный вид, то система представлена в предпочтительном виде. В этом случае легко найти ее опорное решение. Предпочтительные переменные будут базисными, а остальные – свободными. Все свободные переменные нужно приравнять к нулю, тогда базисные переменные будут равны свободным членам. Например, в системе ограничений: предпочтительными (базисными) являются переменные , свободными являются переменные. Приравниваем свободные переменные к нулю, тогда базисные переменные примут значения:,,. Получим начальный опорный план . В случае, когда в каноническом виде с неотрицательной правой частью система ограничений ЗЛП не имеет предпочтительного вида, то начальный опорный план можно найти методом искусственного базиса или методом Жордановых исключений.

Нахождение начального опорного плана злп методом искусственного базиса

В случае, когда ограничение-равенство системы не имеет предпочтительного вида, к его левой части добавляют искусственную переменную . В целевую функцию переменныевводят с коэффициентом «M» в случае решения задачи на минимум и с коэффициентом «–М» в случае решения задачи на максимум, где М – большое (по сравнению с остальными коэффициентами целевой функции) положительное число. Полученная задача называется М-задачей, соответствующей исходной. Она всегда имеет предпочтительный вид. Пусть ЗЛП имеет каноническую форму записи с неотрицательной правой частью: где . Если ни одно из ограничений не имеет предпочтительной переменной, то М-задача запишется так: Тогда начальный опорный план этой задачи: Если некоторое уравнение системы имеет предпочтительный вид, то в него не следует вводить искусственную переменную. Пример 1.13 Найти начальный опорный план ЗЛП методом искусственного базиса и значение целевой функции на этом плане: ; Решение Запишем ЗЛП в каноническом виде с неотрицательной правой частью. ; Составим М-задачу: ; Тогда начальный опорный план: , значение целевой функции на этом плане:. Пример 1.14 Найти начальный опорный план ЗЛП методом искусственного базиса и значение целевой функции на этом плане: ; Решение Запишем ЗЛП в каноническом виде с неотрицательной правой частью. ; Составим М-задачу: ; Тогда начальный опорный план: , значение целевой функции на этом плане:. Пример 1.15 Найти начальный опорный план ЗЛП методом искусственного базиса и значение целевой функции на этом плане: ; Решение Запишем ЗЛП в каноническом виде с неотрицательной правой частью. ; где . Составим М-задачу: ; где . Тогда начальный опорный план: , значение целевой функции на этом плане:.

Источник