Интерполяция и аппроксимация#
Подмодуль scipy.interpolate содержит в себе методы для интерполяции.
Коротко про интерполяцию можно почитать в википедии. Более подробное изложение можно найти в [2] .
Задача интерполирования состоит в том, чтобы по значениям функции \(f(x)\) в нескольких точках отрезка восстановить ее значения в остальных точках этого отрезка. Разумеется, такая задача допускает сколь угодно много решений. Задача интерполирования возникает, например, в том случае, когда известны результаты измерения \(y_h= f(x, k)\) некоторой физической величины \(f(x)\) в точках \(x_k, k = 0, 1, . n\) , и требуется определить ее значения в других точках. Интерполирование используется также при сгущении таблиц, когда вычисление значений \(f(x)\) трудоемко. Иногда возникает необходимость приближенной замены или аппроксимации данной функции другими функциями, которые легче вычислить. В частности, рассматривается задача о наилучшем приближении в нормированном пространстве \(H\) , когда заданную функцию \(f\in H\) требуется заменить линейной комбинацией \(\varphi\) заданных элементов из \(H\) так, чтобы отклонение \(||f—\varphi||\) было минимальным. Результаты и методы теории интерполирования и приближения функций нашли широкое применение в численном анализе, например при выводе формул численного дифференцирования и интегрирования, при построении сеточных аналогов задач математической физики [2] .
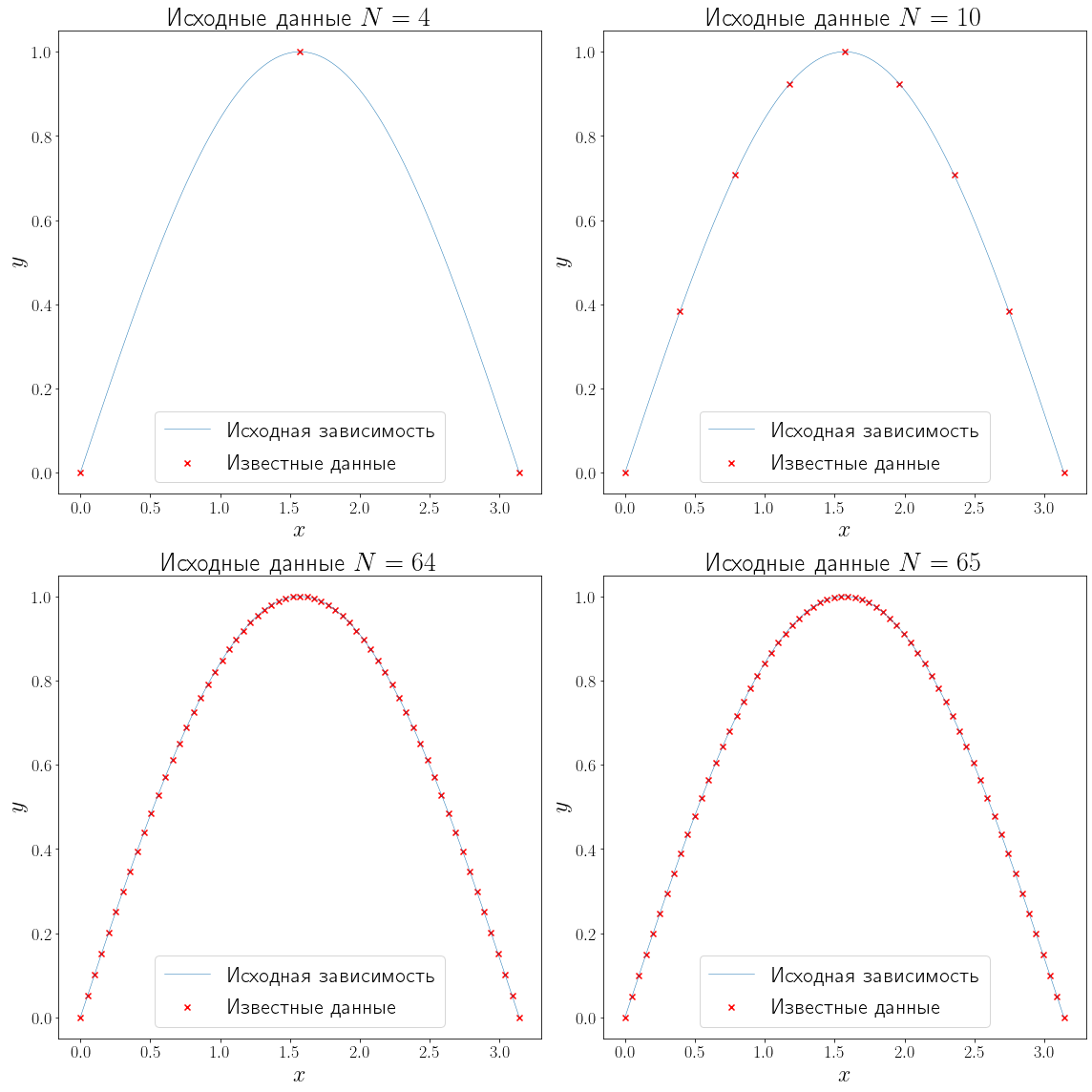
Для того чтобы рассмотреть интерполяцию, сгенерируем данные. Т.е. сгенерируем массив узлов интерполяционной сетки x_data и значений y_data некоторой функции \(f\) в узлах этой сетки при разном количестве известных точек.
import numpy as np L = 0 R = np.pi n_points = (4, 10, 64, 65) f = np.sin xh = np.linspace(L, R, 100) yh = f(xh) def generate_data(f, L, R, n): x_data = np.linspace(L, R, n-1) y_data = f(x_data) return x_data, y_data def plot_problem(ax, x_data, y_data): ax.plot(xh, yh, linewidth=0.5, label="Исходная зависимость") ax.scatter(x_data, y_data, marker="x", color="red", label="Известные данные") ax.set_xlabel("$x$") ax.set_ylabel("$y$") fig, axs = plt.subplots(ncols=2, nrows=2, figsize=(16, 16), layout="tight") for ax, N in zip(axs.flatten(), n_points): x_data, y_data = generate_data(f, L, R, N) plot_problem(ax, x_data, y_data) ax.set_title(f"Исходные данные $N=>$") ax.legend()
Теперь когда данные готовы, осталось произвести интерполяцию. Методов интерполяции существует очень много. Рассмотрим полиномиальную интерполяцию и сплайн интерполяцию.
Полиномиальная интерполяция#
Полиномиальная интерполяция основывается на том факте, что существует единственный полином \(P_(x) = a_0 + a_1 x + \cdots + a_ x ^ N \) степени \(N\) , проходящий через точки \(\<(x_1, y_1), . (x_, y_)\>\) , если \(x_i \neq x_j \quad \forall i, j = 1, \cdots, N + 1, \quad i \neq j\) .
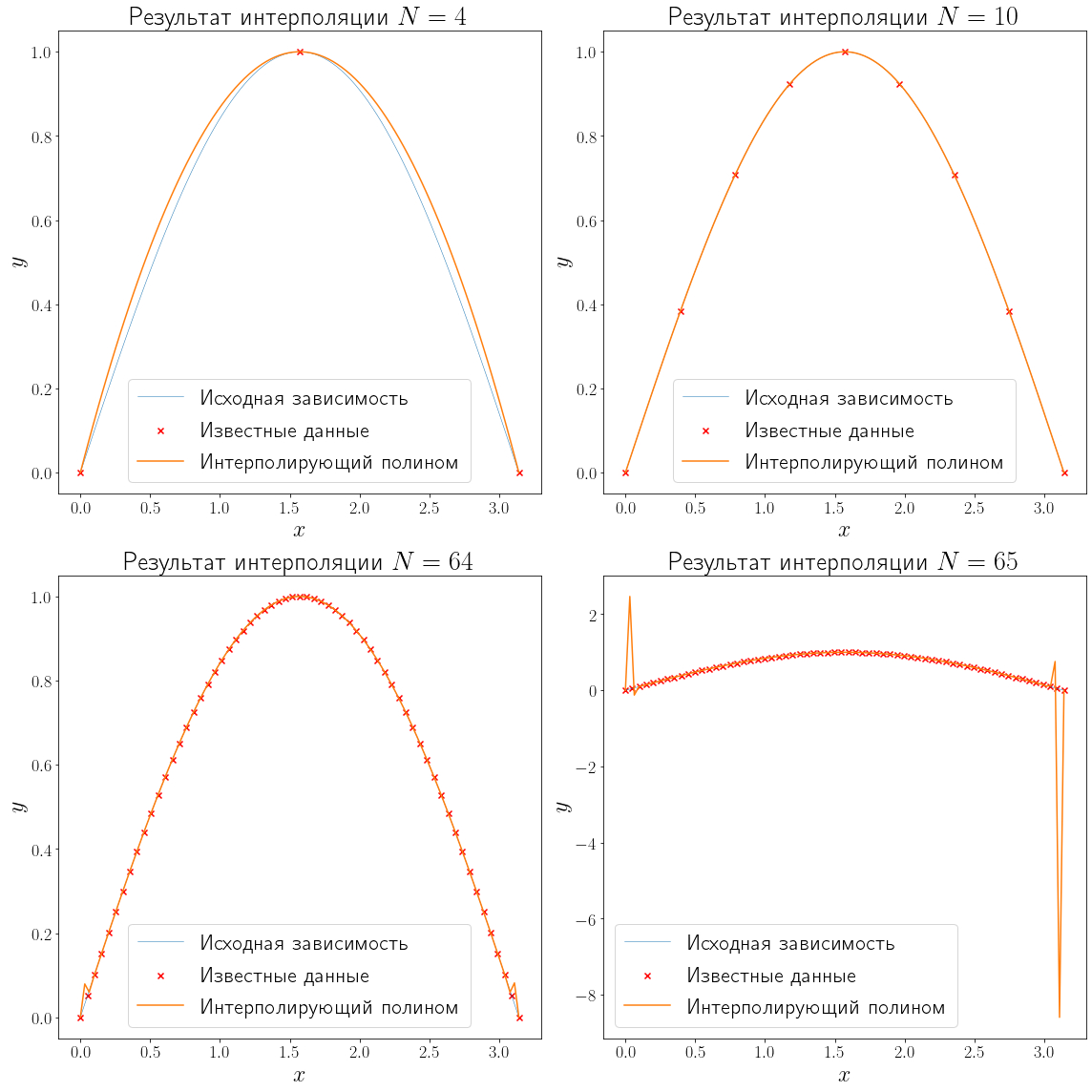
Недостатком полиномиальной интерполяции является её нестабильность. Полиномиальная интерполяция проявляет себя очень плохо при больших \(N\) .
from scipy import interpolate fig, axs = plt.subplots(ncols=2, nrows=2, figsize=(16, 16), layout="tight") for ax, N in zip(axs.flatten(), n_points): x_data, y_data = generate_data(f, L, R, N) plot_problem(ax, x_data, y_data) poly = interpolate.KroghInterpolator(x_data, y_data) y_poly = poly(xh) ax.plot(xh, y_poly, label="Интерполирующий полином") ax.set_title(f"Результат интерполяции $N=>$") ax.legend()
Сплайн интерполяция#
Интерполирование многочленом … на всем отрезке \([a, b]\) с использованием большого числа узлов интерполяции часто приводит к плохому приближению, что объясняется сильным накоплением погрешностей в процессе вычислений. Кроме того, из-за расходимости процесса интерполяции увеличение числа узлов не обязано приводить к повышению точности. Для того чтобы избежать больших погрешностей, весь отрезок \([a, b]\) разбивают на частичные отрезки и на каждом из частичных отрезков приближенно заменяют функцию \(f(х)\) многочленом невысокой степени (так называемая кусочно-полиномиальная интерполяция). Одним из способов интерполирования на всем отрезке является интерполирование с помощью сплайн-функций. Сплайн-функцией или сплайном называют кусочно-полиномиальную функцию, определенную на отрезке \([a, b]\) и имеющую на этом отрезке некоторое число непрерывных производных [2] .
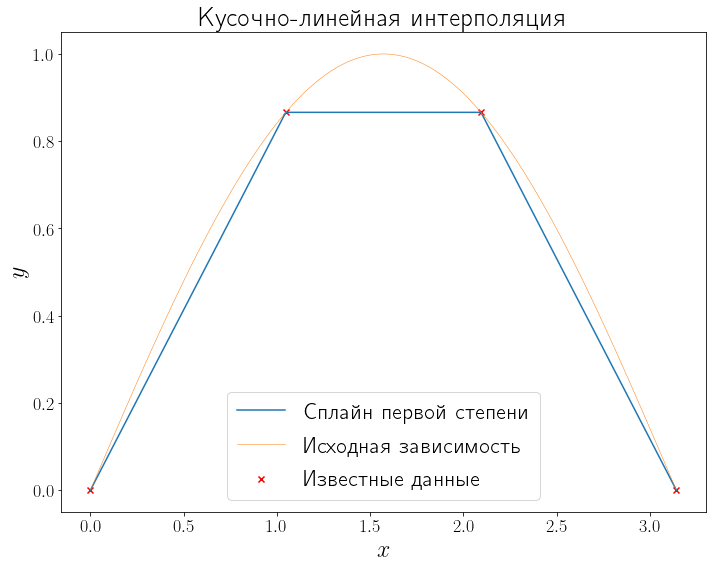
Например, если взять в качестве сплайн-функции полином первой степени, то на выходе получится кусочно-линейная интерполяция.
x_data, y_data = generate_data(f, L, R, 5) linear = interpolate.interp1d(x_data, y_data, kind="linear") y_linear = linear(xh) fig, ax = plt.subplots(figsize=(10, 8), layout="tight") ax.plot(xh, y_linear, label="Сплайн первой степени") plot_problem(ax, x_data, y_data) ax.legend() ax.set_title("Кусочно-линейная интерполяция")
Text(0.5, 1.0, 'Кусочно-линейная интерполяция')
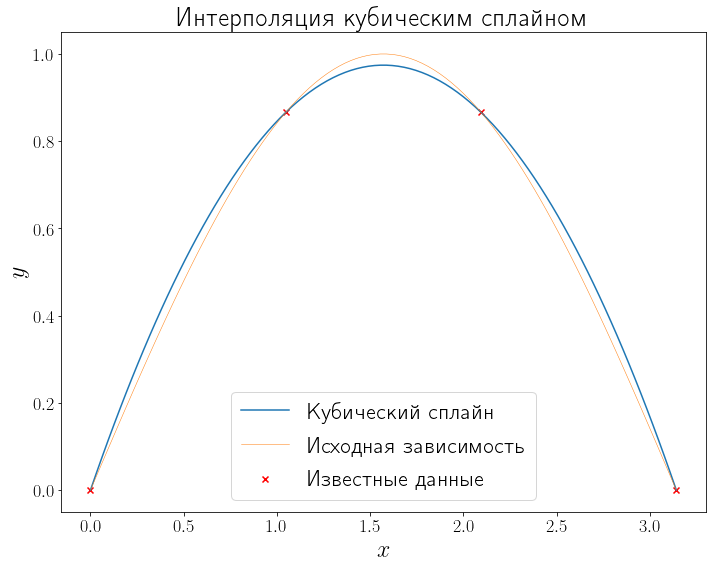
Очень часто выбирают полином третьей степени, которые позволяют строить гладкие интерполирующие полиному и разумно ведут себя между точками во многих случаях.
cubic = interpolate.interp1d(x_data, y_data, kind="cubic") y_cubic = cubic(xh) fig, ax = plt.subplots(figsize=(10, 8), layout="tight") ax.plot(xh, y_cubic, label="Кубический сплайн") plot_problem(ax, x_data, y_data) ax.legend() ax.set_title("Интерполяция кубическим сплайном")
Text(0.5, 1.0, 'Интерполяция кубическим сплайном')
Аппроксимация функций#
При интерполировании ставится цель восстановить исходную зависимость \(y = f(x)\) таким образом по набору точек, через которые функция \(f\) проходит в точности. Но что если значение исходной функции \(f\) в точках \(x_i, \, i=0,\ldots,N\) известно не точно, а в пределах какой-то погрешности или с точностью до какой-то случайной величины, т.е., например, \(y_i = f(x_i) + \varepsilon_i, \, i = 0, \ldots, N\) . В таком случае такое строгое требование на то, чтобы решение \(\varphi(x)\) в точности проходило через все точки \((x_i, y_i), \, i=0, . N\) не имеет большого смысла и может быть ослаблено, например, до поиска такой функции \(\varphi\) из определенного класса функций, которая меньше всего отклоняется от значений \((x_i, y_i),\, i=0. n\) .
Очень распространенным подходом в таком случае является метод наименьших квадратов, при котором отклонение формализуется в виде суммы квадратов отклонений аппроксимирующей функции \(\varphi\) в точках \(x_i, \, i=0,\ldots,N\) от измерений \(y_i, \, i=0,\ldots,N\) . Пусть решение ищется в классе функций \(\\to\mathbb\mid p\in P\>\) , тогда задача аппроксимации сводится к задаче минимизации
\[ \sum_
Многие методы аппроксимации легко обобщаются на многомерные случаи.
При такой постановке часто выделяют линейную и нелинейную аппроксимации. Аппроксимация является линейной, если \(\varphi_p(x)\) линейно зависит от параметров \(p\) .
Аппроксимация функций реализована во множестве других библиотек, таких как statsmodels, scikit-learn и некоторых других.
Линейная аппроксимация#
Очень распространенным случаем линейной аппроксимации является полиномиальная аппроксимация, при которой решение ищется в виде полинома \(P_(x) = a_0 + a_1 x + \cdots + a_ x^n\) , т.е. решается задача
Если все \(x_i, \, i=1,\ldots,N\) все различны, то при \(n=N\) существует глобальный минимум, который соответствует проходящему через все точки интерполирующему полиному, поэтому обычно решение ищется при \(n
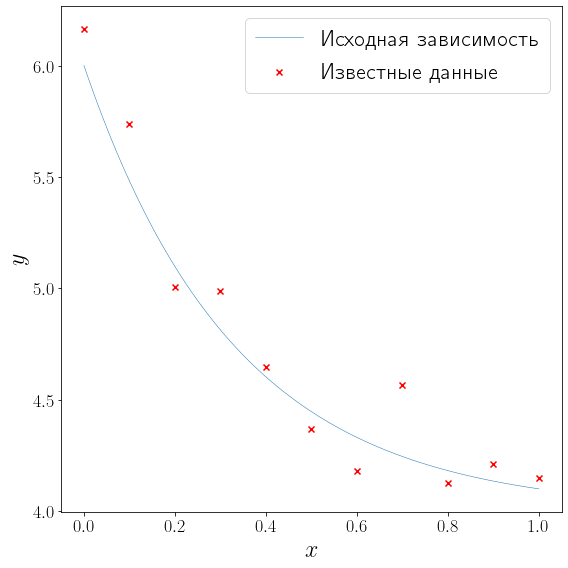
Сгенерируем данные для тестирования полиномиальной интерполяции при различных \(n\) . В качестве исходной зависимости выберем функцию
сгенерируем \(N = 11\) точек \(x_i, \, i=0, \ldots, 10\) равномерно распределенных на отрезке \([0, 1]\) и искусственно добавим распределенный по Гауссу шум к значениям функции \(f\) в этих точках: \(\(0, \sigma^2), \, i=0, \ldots, 10\>\) .
L = 0 R = 1 def f(x): return 2*np.exp(-3*x) + 4 N = 11 sigma = 0.2 x_data = np.linspace(L, R, N) y_data = f(x_data) + np.random.normal(loc=0, scale=sigma, size=N) xh = np.linspace(0, 1, 100) yh = f(xh) fig, ax = plt.subplots(figsize=(8, 8), layout="tight") plot_problem(ax, x_data, y_data) ax.legend()
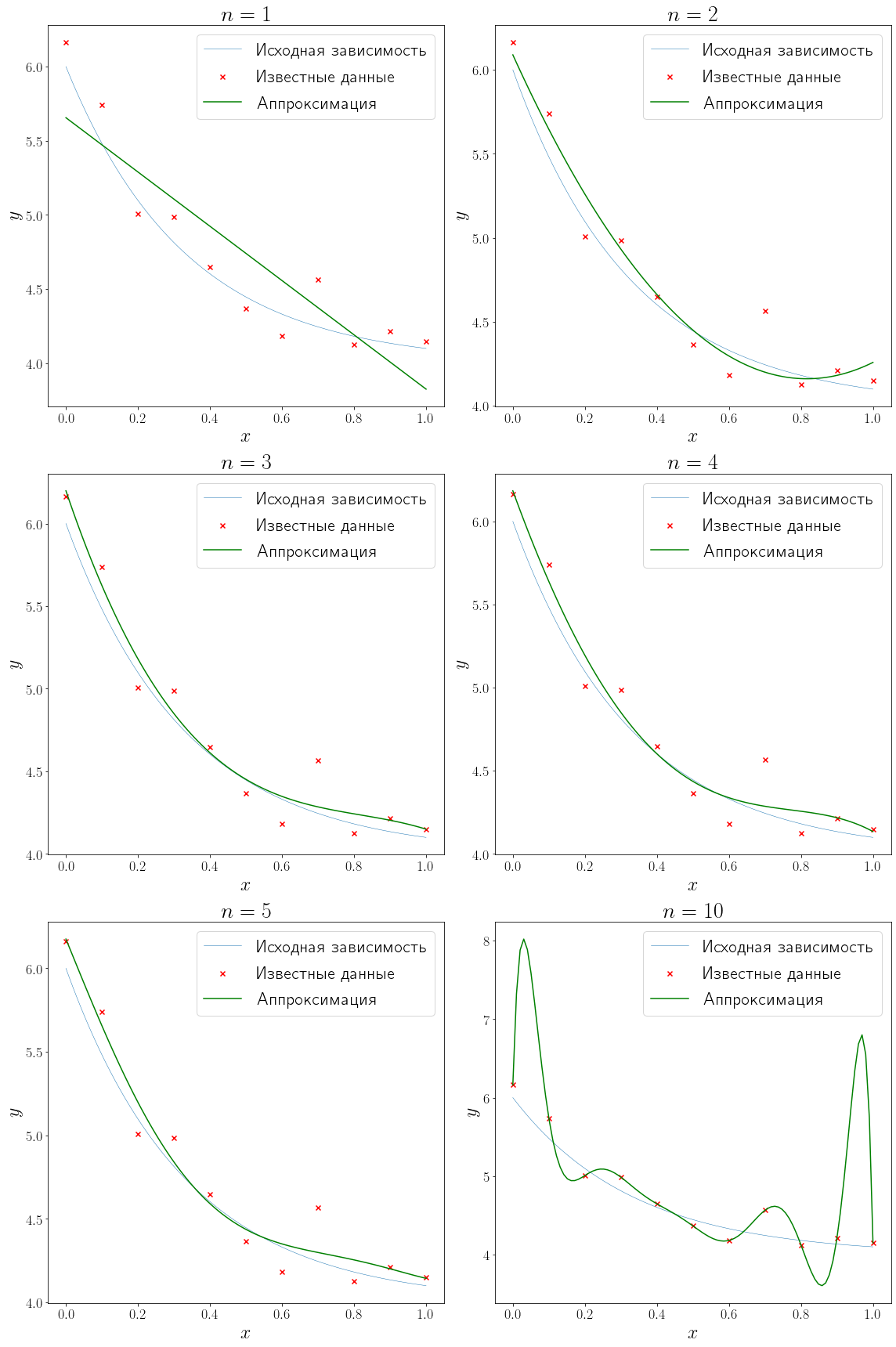
Решить задачу полиномиальной аппроксимации можно средствами модуля numpy.polynomial. В частности подогнать полином заданной степени методом наименьших квадратов можно с помощью метода numpy.polynomial.Polynomial.fit.
from numpy.polynomial import Polynomial degrees = (1, 2, 3, 4, 5, 10) fig, axs = plt.subplots(figsize=(16, 24), nrows=3, ncols=2, layout="tight") for ax, degree in zip(axs.flatten(), degrees): approximation = Polynomial.fit(x_data, y_data, degree) plot_problem(ax, x_data, y_data) ax.plot(xh, approximation(xh), color="green", label="Аппроксимация") ax.set_title(f"$n = degree>$") ax.legend()
В более общем случае при линейной аппроксимации решение ищется в виде линейной комбинации любых функций \(\varphi(x) = c_1\varphi_1(x) + \cdots + c_n\varphi_n(x)\) и задача аппроксимации сводится к подбору коэффициентов \(c_i, \, i=1,\ldots,n\) посредством минимизации
Полиномиальная интерполяция получается при \(\varphi_i(x) = x^i\) . Можно показать, что решение оптимизационной задачи выше эквивалентно минимизации невязки системы линейных алгебраических уравнений
\[\begin
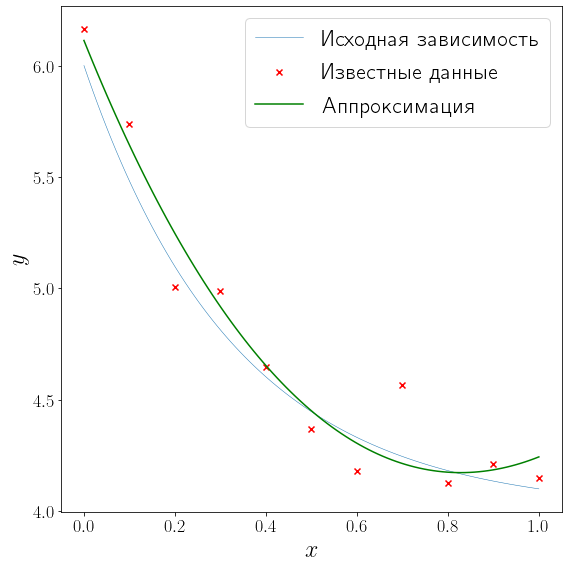
За решение таких задач отвечает метод linalg.lstsq. В качестве примера аппроксимируем тот же набор точек, но решение будем искать в виде
from scipy import linalg def approximation(x, alpha, beta, gamma): return alpha + beta*np.exp(-x) + gamma*np.square(x) A = np.vstack([ np.ones_like(x_data), np.exp(-x_data), np.square(x_data) ]).T b = y_data (alpha, beta, gamma), *_ = linalg.lstsq(A, b) fig, ax = plt.subplots(figsize=(8, 8), layout="tight") plot_problem(ax, x_data, y_data) ax.plot(xh, approximation(xh, alpha, beta, gamma), color="green", label="Аппроксимация") ax.legend()
Нелинейная аппроксимация#
Будем аппроксимировать данные функцией вида
Исходная функция \(f(x)=2e^ + 4\) совпадает с \(\varphi_(x)\) при \(\alpha=2\) , \(\beta=-3\) и \(\gamma=4\) , т.е. теоретически можно восстановить точное решение. Аппроксимация не является линейной, т.к. \(\varphi_\) зависит от параметра \(\beta\) экспоненциально. Метод optimize.curve_fit позволяет искать приближенное решение задачи нелинейной аппроксимации.
Чтобы воспользоваться методом optimize.curve_fit , необходимо определить функцию, которая первым своим аргументом принимает \(x\) (может быть скаляром, а может быть и вектором), а остальными аргументами принимает параметры \(p\) . В примере ниже это функция approximation .
Далее этому методу optimize.curve_fit передаётся эта самая функция, данные, под которые эту функцию необходимо подогнать, и начальное приближение \(p_0\) используемое в качестве стартовой точки для подбора параметров, при которых достигается минимальное среднее квадратичное отклонение \(var\varphi_p\) от заданного набора точек.
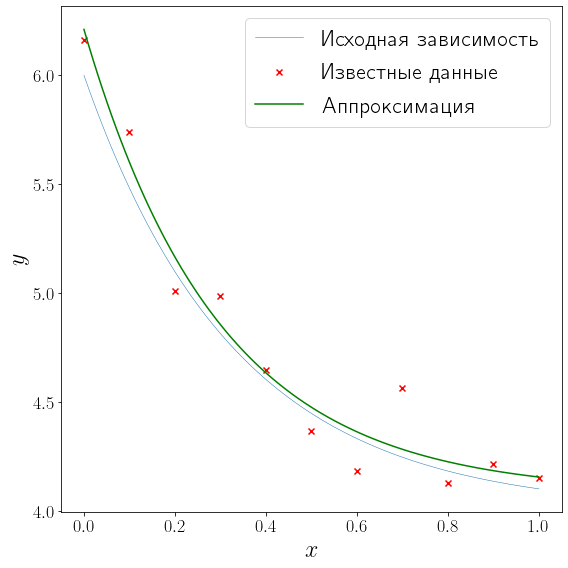
from scipy import optimize def approximation(x, alpha, beta, gamma): return alpha * np.exp(beta * x) + gamma (alpha, beta, gamma), _ = optimize.curve_fit(approximation, x_data, y_data, p0=[3, -6, 10]) fig, ax = plt.subplots(figsize=(8, 8), layout="tight") plot_problem(ax, x_data, y_data) ax.plot(xh, approximation(xh, alpha, beta, gamma), color="green", label="Аппроксимация") ax.legend() print(f""" Найденные параметры: alpha = :.3f>, beta = :.3f>, gamma = :.3f>, """)
Найденные параметры: alpha = 2.130, beta = -3.378, gamma = 4.081,
Видим, что найденные значения коэффициентов \(\alpha, \beta\) и \(\gamma\) с неплохой точностью совпали с истинными и аппроксимирующая кривая довольно близко проходит к исходной \(f(x)\) .
В случае нелинейной аппроксимации следует проявлять особую осторожность, т.к. функционал среднеквадратичного отклонения минимизируется численными методами и начальное приближение \(p_0\) играет большую роль: при не удачном \(p_0\) алгоритм может сойтись не туда или не сойтись вообще.
Список литературы#
Брайан К. Джонс Дэвид Бизли. Python. Книга рецептов. М. ДМК Пресс, 2019. ISBN 978-5-97060-751-0.
Гулин А.В. Самарский А.А. Численные методы. М. Наука, 1989. ISBN 5-02-013996-3.
Решение нелинейных уравнений