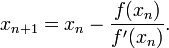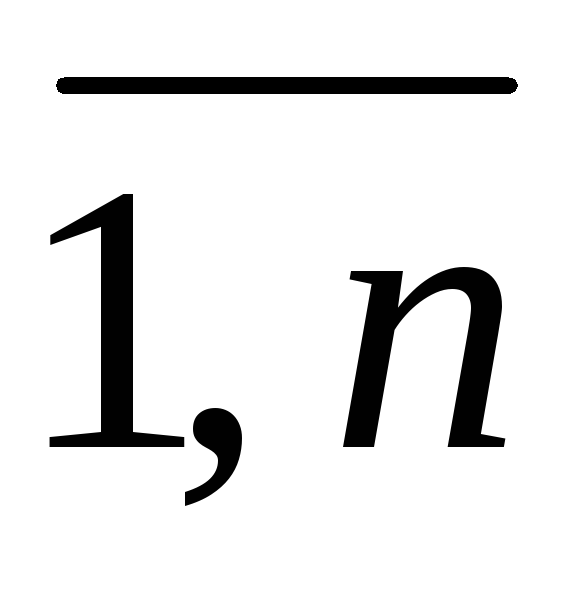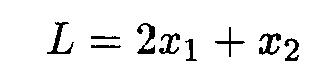Постановка задачи нелинейного программирования целевая функция

Нелинейное программирование. Постановка общей задачи нелинейного программирования

Нелинейное программирование (NLP, англ. NonLinear Programming) — случай математического программирования, в котором целевой функцией или ограничением является нелинейная функция.

Общая задача нелинейного программирования (ОЗНП) определяется как задача нахождения максимума (или минимума) целевой функции f(x₁, х₂. x_n) на множестве D, определяемом системой ограничений

,где хотя бы одна из функций f или g_i является нелинейной.

По аналогии с линейным программированием ЗНП однозначно определяется парой (D, f) и кратко может быть записана в следующем виде

Также очевидно, что вопрос о типе оптимизации не является принципиальным. Поэтому мы, для определенности, в дальнейшем по умолчанию будем рассматривать задачи максимизации.

Как и в ЗЛП, вектор х* = (x₁*,x₂*. x_n*) D называется допустимым планом, а если для любого x D выполняется неравенство f(x*) ≥ f(x), то х* называют оптимальным планом. В этом случае х* является точкой глобального максимума.

С точки зрения экономической интерпретации f(x) может рассматриваться как доход, который получает фирма (предприятие) при плане выпуска х, а g_i(х) ≤ 0 как технологические ограничения на возможности выпуска продукции. В данном случае они являются обобщением ресурсных ограничений в ЗЛП (а_iх – b_i ≤ 0).

Задача (2.2) является весьма общей, т. к. допускает запись логических условий, например:

или запись условий дискретности множеств:

Набор ограничений, определяющих множество D, при необходимости всегда можно свести либо к системе, состоящей из одних неравенств:

либо, добавив фиктивные переменные у, к системе уравнений:

Свойства ЗНП, которые существенно усложняют процесс их решения по сравнению с задачами линейного программирования:

1. Множество допустимых планов D может иметь очень сложную структуру (например, быть невыпуклым или несвязным).

2. Глобальный максимум (минимум) может достигаться как внутри множества D, так и на его границах (где он, вообще говоря, будет не совпадать ни с одним из локальных экстремумов).

3. Целевая функция f может быть недифференцируемой, что затрудняет применение классических методов математического анализа.

В силу названных факторов задачи нелинейного программирования настолько разнообразны, что для них не существует общего метода решения.

Практическая часть Метод Ньютона

Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции.

Чтобы численно решить уравнение f(x)=0 методом простой итерации, его необходимо привести к следующей форме: , где— сжимающее отображение.

Для наилучшей сходимости метода в точке очередного приближения должно выполняться условие. Решение данного уравнения ищут в виде, тогда:

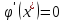
В предположении, что точка приближения «достаточно близка» к корню , и что заданная функция непрерывна, окончательная формула длятакова:

С учётом этого функция определяется выражением:

Эта функция в окрестности корня осуществляет сжимающее отображение, и алгоритм нахождения численного решения уравнения сводится к итерационной процедуре вычисления:

По теореме Банаха последовательность приближений стремится к корню уравнения .

Рис. 2. – Иллюстрация метода Ньютона (синим изображена функция f(x), нуль которой необходимо найти, красным — касательная в точке очередного приближения x_n).

Источник

1.7. Задача нелинейного программирования и условия существования ее решения

называется задачей нелинейного программирования (ЗНЛП), если целевая функция и (или) функции ограничений и в (1.26) являются нелинейными функциями.

В зависимости от вида целевой функции и системы ограничений (1.26), для решения ЗНЛП применяются различные методы. Перед началом поиска решения задачи желательно знать ответ на принципиальный вопрос о его существовании. Достаточные условия существования решения ЗНЛП с ограничениями даются следующей теоремой.

Теорема Вейерштрасса. Пусть допустимое множество задачи (1.25)-(1.26) является непустым и компактным. Тогда непрерывная целевая функция , определенная на этом множестве, достигает глобального максимума (минимума) на внутренней или граничной точке множества .

На рис. 1.2 показаны различные варианты экстремумов функции на компактном одномерном множестве – отрезке

Рис. 1.2. Графическая иллюстрация условных экстремумов

Условия теоремы Вейерштрасса нетрудно проверить, когда решается ЗНЛП с ограничениями. Если же задача не имеет ограничений, то тогда для ее решения применяют классический метод.

1.8. Задачи

Для указанных ниже функций найти все частные производные первого и второго порядка:

Для указанных ниже матриц определить, используя критерий Сильвестра, являются ли они положительно или отрицательно определенными:

Для указанных ниже функций определить, являются ли они выпуклыми или вогнутыми:

13. . 14. . 15. 16.

17. , если . 18. , если .

19. , если . 20. , если .

22. Найти производную функции в точке по направлению к точке .

23. Найти производную функции в точке по направлению к началу координат.

24. Найти производную функции в начале координат в направлении луча, образующего угол с осью .

25. Найти производную функции в точке по направлению к точке .

Для указанных ниже функций найти их стационарные точки:

Найти градиент и матрицу Гессе следующих функций:

Разложить по формуле Тейлора следующие функции в заданной точке с точностью до производных второго порядка:

44. Найти матрицу Якоби вектор-функции в точке .

45. Найти матрицу Якоби вектор-функции в точке .

46. Найти матрицу Якоби вектор-функции в точке .

47. Найти вектор нормали к гиперплоскости, задаваемой уравнением .

48. Найти вектор нормали к гиперплоскости, задаваемой уравнением .

2. Решение задачи нелинейного программирования без ограничений

Необходимо найти либо все максимумы, либо все минимумы целевой функции , либо и то и другое. Ограничений на аргумент целевой функции нет.

Источник

28.1. Общая постановка задачи

Математическая модель задачи нелинейного программиро­вания в общем виде формулируется следующим образом: найти вектор = (х₁, x₂, …, x_n), удовлетворяющий системе ограни­чений

и доставляющий экстремум (наибольшее или наименьшее зна­чение) целевой функции

где x_j — переменные, j = ;L, f, g_i — заданные функции от n переменных, b_i — фиксированные значения.

Нелинейное программирование применяется при прогнози­ровании промышленного производства, управлении товарными ресурсами, планировании обслуживания и ремонта оборудова­ния и т.д.

Для задачи нелинейного программирования в отличие от линейных задач нет единого метода решения. В зависимости от вида целевой функции и системы ограничений разработаны специальные методы решения, к которым относятся методы множителей Лагранжа, квадратичное и выпуклое программи­рование, градиентные методы, приближенные методы реше­ния, графический метод.

Из нелинейного программирования наиболее разработаны задачи, в которых система ограничений линейная, а целевая функция нелинейная. Однако даже для таких задач оптималь­ное решение может быть найдено для определенного класса це­левых функций. Например, когда целевая функция сепарабельная, т.е. является суммой п функций f_j(x_j), или квадратичная. При этом следует отметить, что в отличие от задач линейного программирования, где точками экстремума являются верши­ны многогранника решений, в задачах с нелинейной целевой функцией точки могут находиться внутри многогранника, на его ребре или в вершине.

При решении задач нелинейного программирования для це­левой функции необходимо определить глобальный максимум или глобальный минимум. Глобальный максимум (минимум) функции — это ее наибольшее (наименьшее) значение из ло­кальных максимумов (минимумов).

Наличие локальных экстремумов затрудняет решение за­дач, так как большинство существующих методов нелинейного программирования не позволяет установить, является найден­ный экстремум локальным или глобальным. Поэтому имеется возможность в качестве оптимального решения принять ло­кальный экстремум, который может существенно отличаться от глобального.

28.2. Графический метод

Рассмотрим примеры решения задач нелинейного програм­мирования с двумя переменными, причем их целевые функции и системы ограничений могут быть заданы в линейном и не­линейном виде. Так же как и в задачах линейного программи­рования, они могут быть решены графически.

Задача с линейной целевой функцией и нелинейной системой ограничений

Пример 1. Найти глобальные экстремумы функции

Решение. Область допустимых решений — часть окруж­ности с радиусом 4, которая расположена в первой четверти (рис. 28.1).

Линиями уровня целевой функции являются параллельные прямые с угловым коэффициентом, равным -2. Глобальный минимум достигается в точке O (0, 0), глобальный максимум — в точке А касания линии уровня и окружности. Проведем че­рез точку А прямую, перпендикулярную линии уровня. Прямая проходит через начало координат, имеет угловой коэффициент 1/2 и уравнение x₂ = 1/2х₁.

откуда находим х₁ = 8/5,x₂ = 4/5, L = 16/5 + 4/5 = 4.

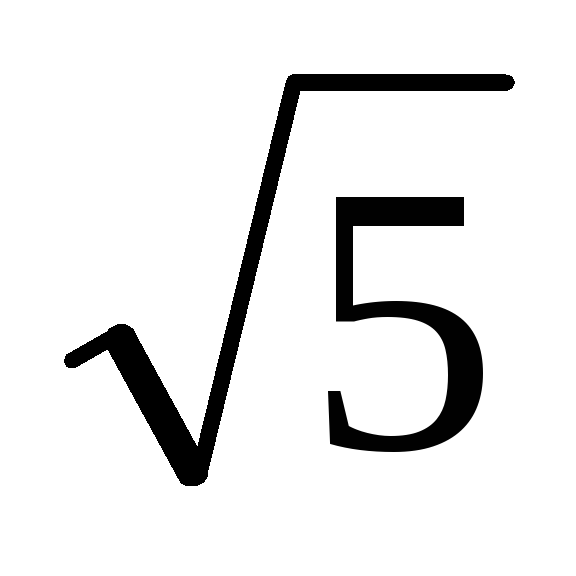
Ответ. Глобальный минимум, равный нулю, достигается в точке O (0, 0), глобальный максимум, равный 4, — в точкеА(8/5, 4/5).

Источник

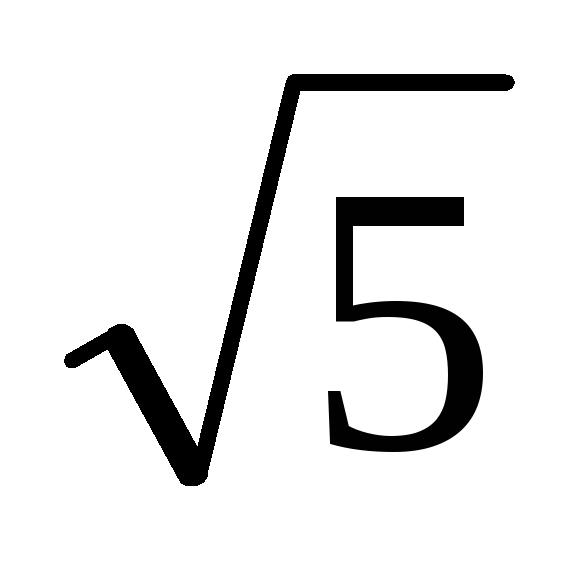
Нелинейное программирование Общая постановка задачи

где x_j – переменные, — заданные функции от п переменных, b_i – фиксированные значения.

Для задачи нелинейного программирования в отличие от линейных задач нет единого метода решения. В зависимости от вида целевой функции и системы ограничений разработаны специальные методы решения, к которым относятся методы множителей Лагранжа, квадратичное и выпуклое программирование, градиентные методы, приближённые методы решения, графический метод.

Графический метод

Рассмотрим примеры решение задач нелинейного программирования с двумя переменными, причём их целевые функции и системы ограничений могут быть заданы в линейном и нелинейном виде. Так же как и в задачах линейного программирования, они могут быть решены графически.

Задача с линейной целевой функцией и нелинейной системой ограничений

Пример 1. Найти глобальные экстремумы функции

ОТВЕТ. Глобальный минимум, равный нулю, достигается в точке О(0, 0), глобальный максимум, равный , — в точке

Задача с нелинейной целевой функцией и линейной системой ограничений

Пример 2. Найти глобальные экстремумы функции

ОТВЕТ. Глобальный максимум, равный 58, достигается в точке D(9, 0), глобальный минимум, равный нулю, — в точке О₁(2, 3).

Пример 3. Найти глобальные экстремумы функции

ОТВЕТ. Глобальный максимум, равный 52, находится в точке О(0, 0). Глобальный минимум, равный 1053/169, находится в точке Е(51/13б21/13).

Задача с нелинейной целевой функцией и нелинейной системой ограничений

Пример 4. Найти глобальные экстремумы функции

ОТВЕТ. Глобальный минимум, равный нулю, достигается в точке О₁(2, 1), глобальный максимум, равный 13, находится в точке А(0, 4).

Пример 5. Найти глобальные экстремумы функции

ОТВЕТ. Целевая функция имеет два глобальных минимума, равных 17, в точках А(1, 4) и В(4, 1), глобальный максимум, равный 2417/49, достигается в точке Е(7, 4/7).

Дробно-линейное программирование

Дробно-линейное программирование относится к нелинейному программированию, так как имеет целевую функцию, заданную в нелинейном виде.

Задача дробно-линейного программирования в общем виде записывается следующим образом:

где — постоянные коэффициенты и

Рассмотрим задачу дробно-линейного программирования в виде

Для решения этой задачи найдём область допустимых решений, определяемую заданными ограничениями. Пусть эта область не является пустым множеством.

Из выражения, задающего целевую функцию, найдём х₂:

Прямая x₂ = kx₁ проходит через начало координат. При некотором фиксированном значении L угловой коэффициент k тоже фиксирован, и прямая займёт определённое положение. При изменении значений L прямая x₂ = kx₁ будет поворачиваться вокруг начала координат.

Установим, как будет вести себя угловой коэффициент k при монотонном возрастании L. Найдём производную от k по L:

Знаменатель производной всегда положителен, а числитель от L не зависит. Следовательно, производная имеет постоянный знак, и при увеличении L угловой коэффициент будет только возрастать или только убывать, а прямая будет поворачиваться в одну сторону. Если имеет положительное значение, то прямая вращается против часовой стрелки, при отрицательном значении — по часовой стрелке. Установив направление вращения, находим вершину или вершины многогранника, в которых функция принимает max (min) значение, либо устанавливаем неограниченность задачи.

При этом возможны следующие случаи.

1. Область допустимых решений ограничена, максимум и минимум достигаются в её угловых точках (рис. а).

2. Область допустимых решений неограниченна, однако существуют угловые точки, в которых целевая функция принимает максимальное и минимальное значения (рис. б).

3. Область допустимых решений неограниченна, имеется один из экстремумов. Например, минимум достигается в одной из вершин области и имеет так называемый асимптотический максимум (рис. в).

4. Область допустимых решений неограниченна. Максимум и минимум являются асимптотическими (рис. г).

Источник