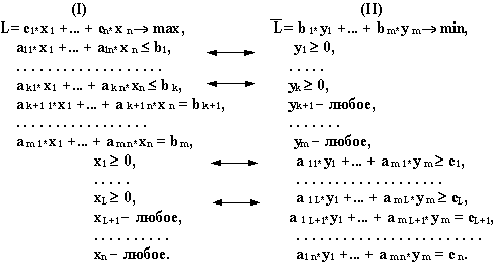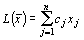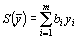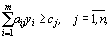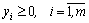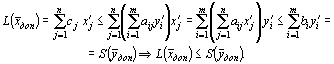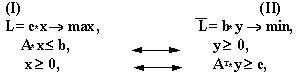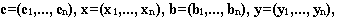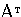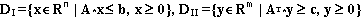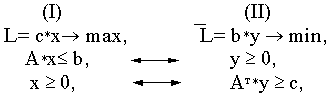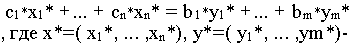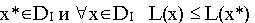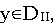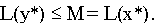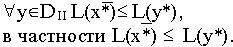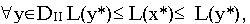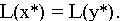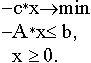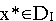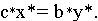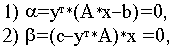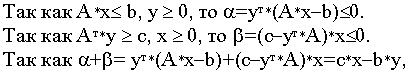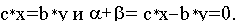Определение двойственных задач линейного программирования

§8. Постановка двойственной задачи линейного программирования. Типы двойственных задач линейного программирования

Каждой ЗЛП можно определённым образом сопоставить некоторую другую задачу, называемую двойственной (или сопряжённой) по отношению к исходной задаче.

Рассмотрим пример, показывающий, как в реальной экономичес­кой ситуации появляются взаимно двойственные задачи линейного программирования [8]. На некотором предприятии после выполнения годового плана возник вопрос – как поступить с остатками сырья? У руководства и экономистов предприятия возникли два пути решения: либо продать остатки сырья какой-нибудь нуждающейся в нем организации (наиболее простой вариант), либо наладить из оставшегося сырья производство каких-то изделий на своем собственном оборудовании.

Для простоты будем считать, что имеются два вида сырья S₁ и S₂, остатки которого составляют соответственно и единиц. Из этого сырья можно наладить производство трех видов товаров: Т₁, Т₂, Т₃. От реализации одной единицы каждого вида товара Т₁, Т₂, Т₃ предприятие полу­чит прибыль соответственно , , у.е. Нормы расхода сырья на производство товаров Т₁, Т₂, Т₃ вместе с данными о при­были и запасах представлены в следующей таблице, где означает, сколько единиц сырья расходуется на производство товара .

Проследим за ходом мыслей экономистов предприятия. Как уже гово­рилось, им предстояло проанализировать две возможности.

При исследовании второй возможности (наладить выпуск товаров Т₁, Т₂, Т₃) возникает вопрос о плане выпуска товаров. План выпуска задается тремя числами , где – количество единиц товара , которое следует произвести ( ). Неизвестные должны удовлетворять системе ресурсных ограничений

причем прибыль, которую получит предприятие от реализации оптимального плана выпуска товаров, должна быть максимальной:

Следо­вательно, чтобы наилучшим образом использовать вторую возможность, нужно решить задачу линейного программирования (8.1), (8.2).

Исследуем теперь первую возможность – продать сырье другой организации. Здесь возникает вопрос: по каким ценам продавать сырье? Обозначим эти цены , где – цена единицы сырья S_i ( ).

Справедливое требование к ценам со стороны продающего пред­приятия состоит в следующем. Если взять сырье, идущее на изготов­ление единицы товара Т_i ( ), то выручка от его продажи должна быть не меньше, чем прибыль от реализации готового изделия (в противном случае нет смысла продавать сырье – лучше изго­товить из него товар и получить за него прибыль). Это требование приводит к системе неравенств

Первое из написанных неравенств в системе (8.3) означает, что вы­ручка от продажи единиц сырья S₁ и единиц сырья S₂ (именно такое количество сырья расходуется на изготовление единицы товара T₁) не мень­ше, чем прибыль, которую могло бы получить предприятие от про­дажи единицы товара T₁, если бы оно отказалось от идеи продать сырье и занялось изготовлением из него товаров T₁, T₂, T₃. Анало­гичный смысл имеют остальные два неравенства.

Что же касается покупателя, то для него единствен­ное пожелание заключается в сокращении до минимума расходов на покупку сырья:

Итак, для оптимального использования первой воз­можности необходимо решить задачу линейного программирования (8.3), (8.4).

Для наглядности сопоставим формулировки двух задач:

Задача (8.1), (8.2) и задача (8.3), (8.4) в линейном программировании называются двойственными друг другу. При этом задачу (8.1), (8.2) называют прямой задачей.

Рассмотрим основные типы двойственных задач линейного программирования. Пусть прямая задача линейного программирования имеет вид

Запишем эту задачу в матричном виде

где – вектор-столбец коэффициентов целевой функции, – вектор-столбец управляющих переменных, – матрица коэффициентов при управляющих переменных, – вектор-столбец свободных членов.

Тогда соответствующая двойственная задача линейного программирования к прямой задаче (8.5) имеет вид

где – вектор-столбец управляющих переменных двойственной задачи.

Определение 8.1. Пару прямой (8.5) и двойственной (8.6) ЗЛП называют симметричной.

Симметрические двойственные ЗЛП составляются в том случае, когда в системе ограничений прямой ЗЛП стоят только все знаки , или только все знаки .

Приведем алгоритм построения симметрических двойственных ЗЛП.

1) Каждому неравенству системы ограничений прямой ЗЛП (8.5) поставить в соответствие неотрицательную переменную (число управляющих переменных двойственной задачи равно числу функциональных ограничений прямой задачи).

2) В качестве коэффициентов целевой функции двойственной ЗЛП взять свободные члены системы ограничений прямой задачи.

3) Направление оптимизации (тип экстремума) целевой функции двойственной задачи противоположно направлению оптимизации целевой функции прямой задачи (если прямая задача была на максимум, то двойственная задача – на минимум, и наоборот).

4) Пусть – матрица коэффициентов системы ограничений прямой ЗЛП. Получить матрицу коэффициентов системы ограничений двойственной ЗЛП из матрицы транспонированием: . Число ограничений в системе ограничений двойственной ЗЛП равно числу переменных прямой ЗЛП.

5) В качестве свободных членов системы ограничений двойственной задачи взять коэффициенты целевой функции прямой задачи.

6) В двойственной задаче на максимум задать знаки для всех неравенств-ограничений, в задаче на минимум – .

Пример 8.1. Построить двойственную ЗЛП для задачи

Решение. Матричная форма записи данной ЗЛП имеет вид (см. (8.5))

где – вектор-столбец коэффициентов целевой функции ,

– вектор-столбец управляющих переменных, – матрица коэффициентов при управляющих переменных, – вектор-столбец свободных членов.

Тогда соответствующая ДЗЛП запишется в виде (см. (8.6))

, где – вектор-столбец управляющих переменных двойственной задачи.

Рассмотрим ЗЛП канонического вида в матричном виде

Тогда соответствующая двойственная ЗЛП к (8.7) имеет вид

где – вектор-столбец управляющих переменных двойственной задачи, причем компоненты в общем случае произвольного знака (в том числе и отрицательного знака).

Определение 8.2. Пару прямой (8.7) и двойственной (8.8) ЗЛП называют несимметричной.

Определение 8.3. Пару прямой и двойственной ЗЛП называют смешанной, если система ограничений прямой задачи имеет как знаки строго равенства (знак =), так и знаки , .

При составлении смешанной пары двойственных задач руководствуются алгоритмом составления симметрической пары. Если функциональное ограничение прямой задачи имеет знак неравенства , то соответствующая этому ограничению переменная двойственной задачи следует считать неотрицательной. Если же функциональное ограничение прямой задачи является равенством, то соответствующая переменная двойственной задачи может принимать как положительные, так и отрицательные значения.

Пример 8.2. Построить двойственную ЗЛП для задачи

Решение. Соответствующая ДЗЛП имеет вид

Источник

9) Двойственные задачи. Двойственность в линейном программировании. Правила построения двойственных задач

Двойственная задача линейного программирования — формальная модель задачи линейного программирования, симметричная к исходной постановке в части управляемых переменных, коэффициентов целевой функции и ограничений.

Для ряда практических задач линейного программирования целесообразно заменить решение исходной прямой задачи решением соответствующей двойственной задачи, симметричной исходной. Для любой прямой задачи линейного программирования можно сформулировать двойственную задачу следующим образом.

Прямая задача: CX -> min при условиях AX >= B X >= 0

Двойственная задача: YB -> max при условиях YA =< C Y >= 0

В приведенной матричной формулировке симметричность обеих задач очевидна. При этом также очевидно, что задача двойственная к двойственной есть исходная прямая задача. Таким образом, из данной пары можно считать любую задачу прямой, а другую двойственной.

Из сравнения обеих задач видно, что:

1. Если в исходной задаче имеется n переменных и m ограничений, то в двойственной m переменных и n ограничений.
2. Матрица коэффициентов ограничений двойственной задачи получается транспонированием соответствующей матрицы прямой задачи.
3. В правых частях ограничений каждой задачи стоят коэффиценты целевой функции, взятой из другой задачи.
4. Знаки неравенств функциональных ограничений обеих задач являются взаимно-обратными.
5. Если в прямой задаче требуется минимизация целевой функции, то в двойственной задаче требуется максимизация целевой функции.

Правила построения пары двойственных задач

Рассмотрим пару задач ЛП вида:

Задачу (I) называют прямой задачей ЛП, а (II) — двойственной. Ограничения задач (I) и (II), соответствующие друг другу (по стрелке), называются сопряженными. Заметим, что задача двойственная к (II), есть исходная прямая задача, т.е. соотношение двойственности взаимное. Поэтому можно любую из такой пары задач считать прямой, а другую двойственной.

Грубо говоря, двойственная задача — это на 90 0 повернутая исходная прямая задача. В этой связи полезно усвоить следующую схему соответствия.

10) Три леммы о двойственных задачах. Первая теорема двойственности. Следствия.

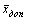
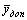
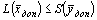
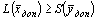
Лемма 1. Если и — произвольные допустимые решения пары двойственных задач, то , если исходная задача на максимум, и , если она на минимум.

Доказательство. Дана симметричная пара двойственных задач:

исходная задача: найти максимум функции

₍₄₎

и (5)

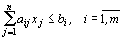
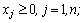
двойственная задача: найти минимум функции

₍₆₎

₍₇₎

.

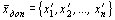
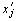
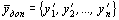
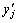
Пусть — допустимое решение исходной задачи, т.е. удовлетворяют неравенствам (5), — допустимое решение двойственной задачи, т.е. удовлетворяют неравенствам (7).

Аналогично рассматривается случай минимума.

Лемма 2. Достаточный признак оптимальности.

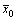
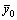
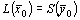
Если и — допустимые решения пары двойственных задач, для которых выполняется равенство , то и — оптимальные решения соответствующих задач.

Доказательство. Пусть и — допустимые решения пары двойственных задач, причем , и пусть исходная задача решается на максимум.

Возьмем произвольное допустимое решение исходной задачи , тогда по первой лемме . Получим т.е. , следовательно, — оптимальное решение исходной задачи. Аналогично доказывается, что — оптимальное решение двойственной задачи.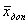

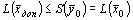
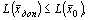
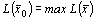
Рассмотрим пару симметрических двойственных задач в матричной форме записи

А- матрица из m строк и n столбцов, — транспонированная матрица. Введем обозначения для допустимых областей задачи (I) и (II)

Первая теорема двойственности

Рассмотрим пару симметричных двойственных задач

Первая теорема двойственности.

Если одна из пары двойственных задач (I) и (II разрешима, то разрешима и другая задача, причем оптимальные значения целевых функций прямой и двойственной задач совпадают

оптимальные планы задач (I) и (II) соответственно.

1. Пусть задача (I) разрешима, и пусть

т.е. х* — оптимальное решение. Обозначим M= L(х*).

Тогда по основной лемме существует

для которого

Но по основному неравенству двойственности имеем :

Объединяя последние два соотношения, имеем

откуда следует, что у* — оптимальное решение задачи (II) и

2. Пусть теперь задача (II) -разрешима. Построим эквивалентную (II) задачу

Задача (II’) разрешима, так как задача (II) разрешима. Тогда по пункту 1 двойственная к (II’) задача :

Но эта задача эквивалентна задаче (I). Следовательно, задача (I) разрешима.

Первый критерий оптимальности

Решение оптимально тогда и только тогда, когда существует решение

такое, что

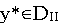
Необходимость следует из первой теоремы двойственности.

Достаточность следует из достаточного условия оптимальности.

11) Вторая теорема двойственности. Анализ чувствительности решений. Теорема о маргинальных значениях. Симплекс-множители.

Рассмотрим пару симметрических двойственных задач ЛП

Вторая теорема двойственности

Чтобы допустимые решения х, у пары двойственных задач (I) и (II) были оптимальными необходимо и достаточно, чтобы выполнялись условия :

Необходимость. По условию допустимые решения х, у — оптимальны.

то из оптимальности решений х, у по первой теореме двойственности

В результате имеем

По первой теореме двойственности получаем, что х, у — оптимальные решения задач (I) и (II).

Допустимые решения х, у задач (I) и (II) удовлетворяют условиям дополняющей нежесткости (УДН), если при подстановке этих векторов в ограничения задач (I) и (II) хотя бы одно из любой пары сопряженных неравенств обращается в равенство

Источник