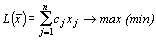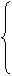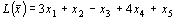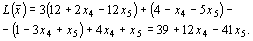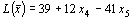- Общая, стандартная и основная задачи линейного программирования
- Геометрическая интерпретация задачи линейного программирования
- Общая и основная задачи линейного программирования.
- Свойства задач линейного программирования. Графический метод решения задач линейного программирования.
- Определение задачи линейного программирования (злп), общая, симметричная и каноническая формы записи задачи линейного программирования
- Переход от одной формы злп к другой
- Математические модели экономических задач Задача об оптимальном использовании ресурсов
Общая, стандартная и основная задачи линейного программирования
Определение 1. Общей задачей ЛП называется задача нахождения максимального (минимального) значения линейной целевой функции 













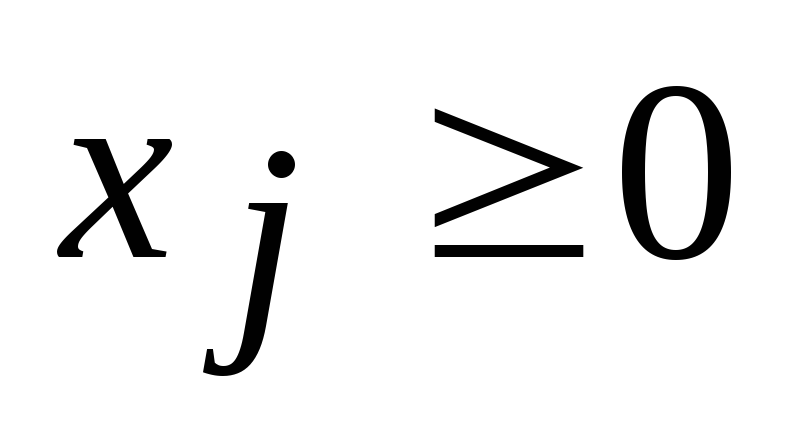





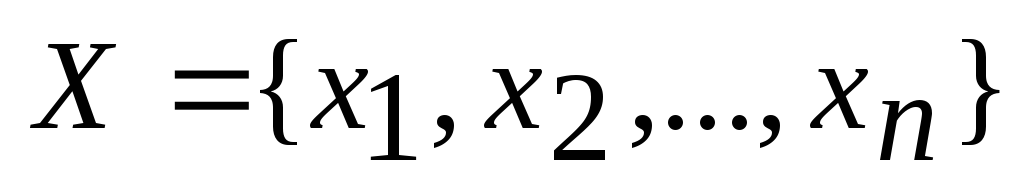


- Задачу минимизации функции можно свести к задаче максимизации, и, наоборот, путем замены знаков коэффициентов
на противоположные, поскольку
.
- Ограничения-неравенства (2) можно заменить эквивалентными ограничениями-равенствами путем введения дополнительных неотрицательных переменных следующим образом:
Ограничение-неравенство вида 




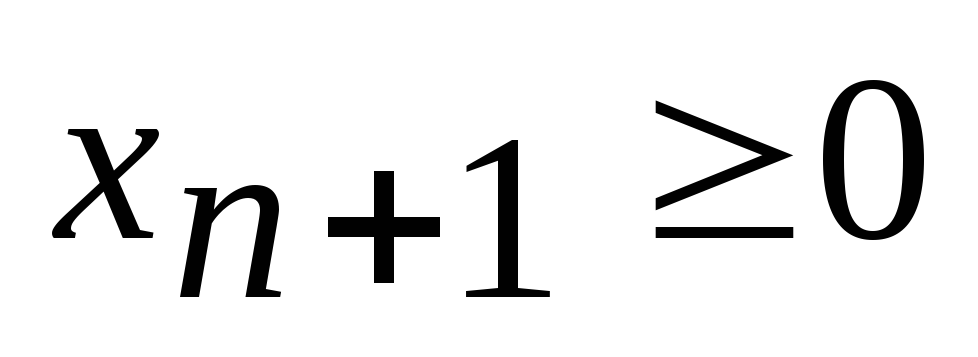
- Каждое ограничение-равенство вида (3) можно записать в виде двух неравенств
.
- Переменная
, неограниченная условием неотрицательности вида (4), можно заменить разностью двух дополнительных неотрицательных переменных:
,
,
.
-
Геометрическая интерпретация задачи линейного программирования
Рассмотрим задачу, состоящую в определении максимального значения функции: 









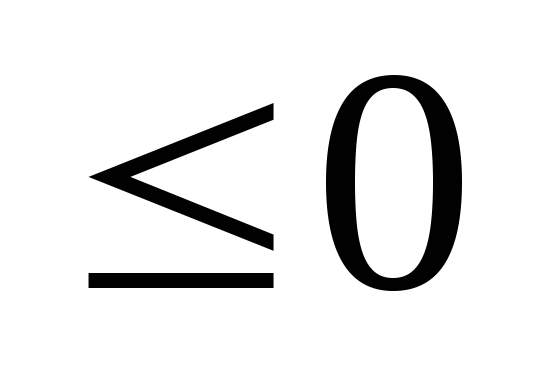


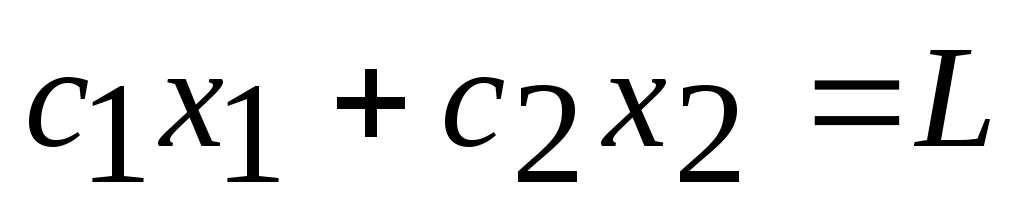
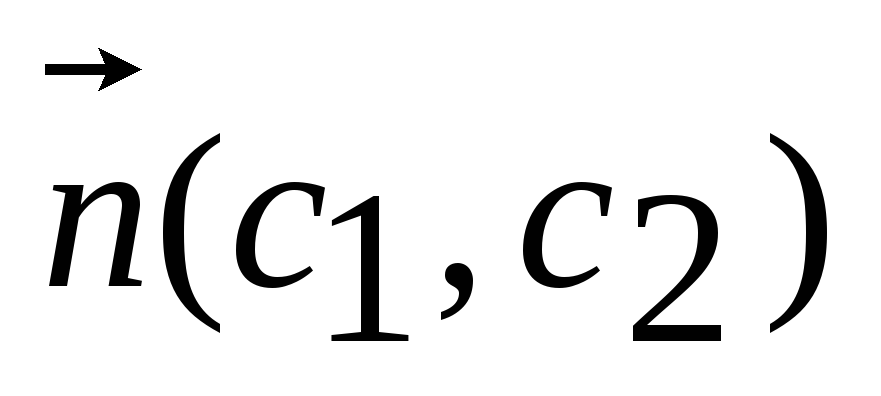

Общая и основная задачи линейного программирования.
Общая задача. Найти максимальное значение линейной целевой функции. z = c1x1+ c2x2+ … + cnxn при линейных ограничениях xj>= 0,j= 1,n= n> Определение 1.1. Совокупность чисел х = (х1, х2. хn), удовлетворяющих ограничениям (1.2), называется допустимым решением или планом. Определение 1.2. План х* =(х1 * , х2 * . хn*), при котором целевая функция (1.1) принимает свое максимальное значение, называется оптимальным.Каноническая форма. Задачу линейного программирования будем считать приведенной к каноническому виду, если 1) требуется найти максимум целевой функции; 2) система ограничений (1.2) содержи! только равенства; 3) правые части системы ограничений неотрицательны. Переход от общей формы к канонической: 1) если в задаче требуется найти минимум целевой функции, то вводим новую целевую функцию z1 = -z, тогда max z1 = -min z; 2) чтобы перейти от неравенства к равенству в системе ограничений, необходимо прибавить (вычесть) дополнительную неотрицательную переменную к левой части неравенства; 3) если в правой части системы ограничений имеются отрицательные числа, то необходимо умножить на «-1» обе части равенства, в котором в правой части стоит отрицательное число. Задачу линейного программирования в канонической форме называют основной задачей.
Свойства задач линейного программирования. Графический метод решения задач линейного программирования.
Свойства задач линейного программирования. Рассмотрим следующую основную задачу линейного программирования: z = c1x1+ c2x2+ …+cnxnmax при ограничениях 

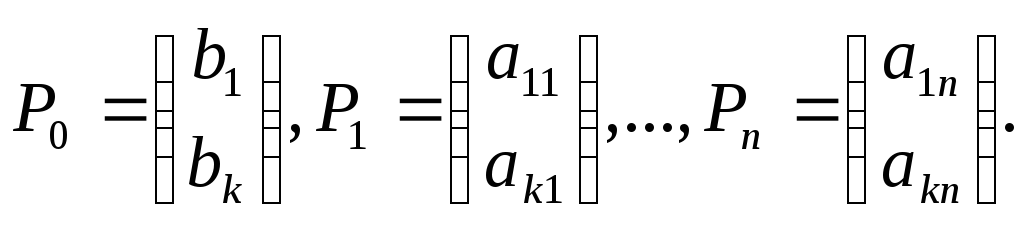

Определение задачи линейного программирования (злп), общая, симметричная и каноническая формы записи задачи линейного программирования



называется общей задачей линейного программирования (ЗЛП).
Задача в краткой записи имеет вид
,
Определение 2. Задача, в которой требуется найти экстремум функции
,
называется задачей линейного программирования, заданной в канонической форме.
Определение 3. Задача, в которой требуется найти экстремум функции
,
называется задачей линейного программирования заданной в симметричной форме записи.
Определение 4. Функция
называется целевой функцией ЗЛП.
Определение 5. Совокупность чисел удовлетворяющая ограничениям ЗЛП, называется допустимым решением ЗЛП.
Определение 6. Допустимое решение, при котором целевая функция принимает максимальное (минимальное) значение, называется оптимальным решением ЗЛП.
Переход от одной формы злп к другой
Переход от неканонической формы ЗЛП к канонической.
Теорема 1. Каждому решению 
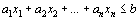



Из теоремы следует, что неравенство 


Переменную называют балансовой переменной.
Следовательно, чтобы привести задачу к каноническому виду, нужно заменить каждое неравенство системы ограничений соответствующим уравнением и неравенством , введя в каждое неравенство балансовую переменную с коэффициентом +1, если знак неравенства £, и с коэффициентом -1, если знак неравенства ³. В целевую функцию балансовые переменные вводятся с нулевыми коэффициентами.
Если на переменную 


Переход от канонической формы ЗЛП к симметричной форме.
Чтобы перейти от канонической формы ЗЛП к симметричной, нужно найти общее решение системы уравнений:
Так как все переменные должны быть неотрицательными, в том числе и базисные, получим систему неравенств:
Чтобы исключить базисные переменные из целевой функции, необходимо в целевую функцию вместо базисных переменных подставить их выражения через свободные переменные.
Пример 1. Дана ЗЛП: найти наибольшее значение функции при ограничениях:
.
Приведем ее к каноническому виду.
Канонический вид задачи: найти наибольшее значение функции при ограничениях:
.
Пример 2. Перейти от канонического вида задачи к симметричному. Найти наибольшее значение функции при ограничениях:
.
Разрешим систему относительно произвольного базиса, система примет вид
И так как 

Выразим целевую функцию через свободные переменные:
Симметричный вид задачи: найти наибольшее значение функции при ограничениях:
.
Математические модели экономических задач Задача об оптимальном использовании ресурсов
Предприятие может выпускать определенные виды продукции, используя для этого различные виды ресурсов. Известны затраты каждого вида ресурса на производство единицы каждого вида продукции и прибыль от реализации единицы каждого вида продукции. Требуется составить план выпуска продукции, чтобы при данных запасах ресурсов получить максимальную прибыль.
Составим математическую модель данной задачи.
i — номер i-го вида ресурса, ;
bi — запасы i-го вида ресурса, ;
j — номер j-го вида продукции, ;
aij — затраты i-го вида ресурса на производство единицы j-го вида продукции;
cj — прибыль от реализации единицы j-го вида продукции.
Все данные занесем в таблицу:
1 2 … j … n




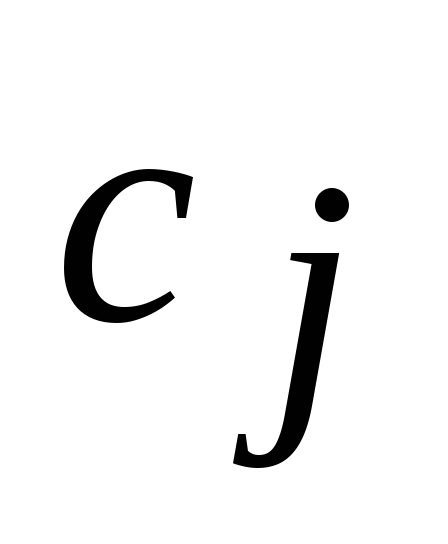 на противоположные, поскольку
на противоположные, поскольку .
. .
. , неограниченная условием неотрицательности вида (4), можно заменить разностью двух дополнительных неотрицательных переменных:
, неограниченная условием неотрицательности вида (4), можно заменить разностью двух дополнительных неотрицательных переменных: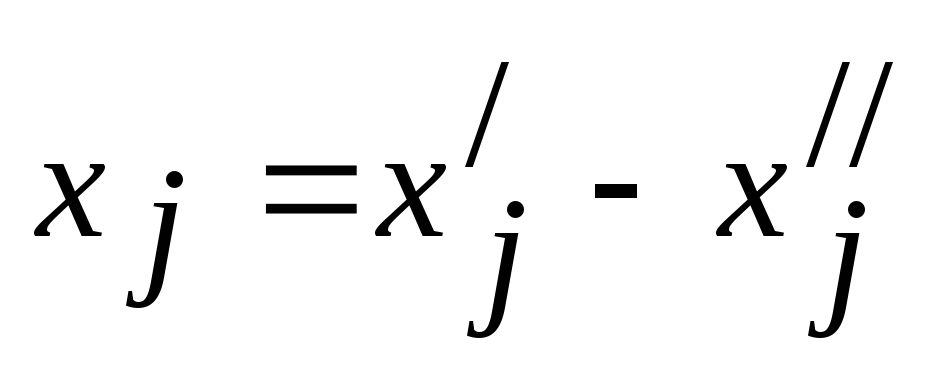 ,
, ,
,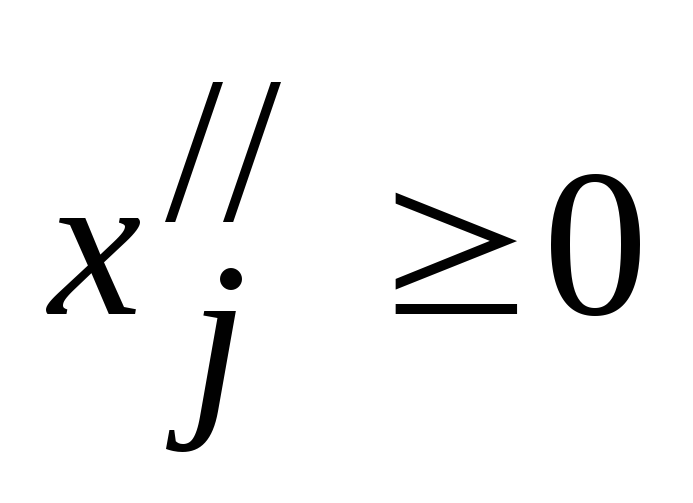 .
.