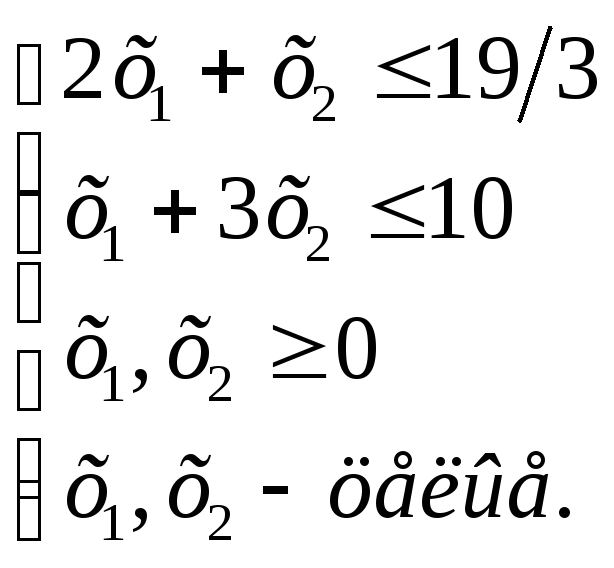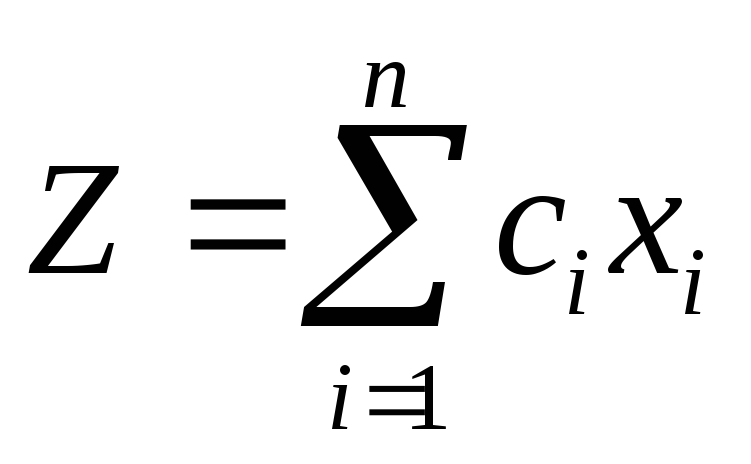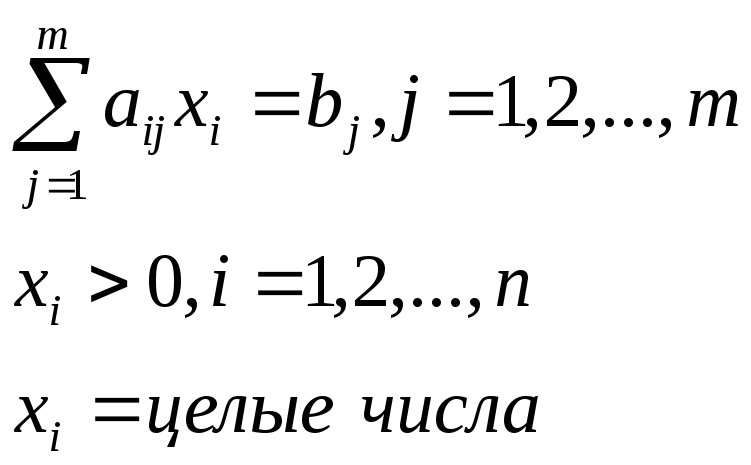Общая постановка задачи целочисленного программирования

Лекция 10 Целочисленное программирование

Оптимальное решение задачи, найденное симплексным методом, часто не является целочисленным. Его можно округлить до ближайших целых чисел. Однако такое округление может дать решение, не лучшее среди целочисленных решений, или привести к решению, не удовлетворяющему системе ограничений. Поэтому для нахождения целочисленного решения существует специальный алгоритм, который предложен Гомори.

Симплексным методом находят оптимальное решение задачи. Если решение целочисленное, то задача решена. Если же оно содержит хотя бы одну дробную координату, то накладывают дополнительное ограничение по целочисленности и вычисления продолжают до получения нового решения. Если и оно является нецелочисленным, то вновь накладывают дополнительное ограничение по целочисленности. Вычисления продолжают до тех пор, пока не будет получено целочисленное решение или показано, что задача не имеет целочисленного решения.

где r – ранг системы ограничений; h_i,r+1 – коэффициенты симплексной таблицы i-й строки, (r+1)-го столбца; f_i – свободный член i-й строки.

Пусть f_i и хотя бы одно h_ij ( ) – дробные числа.

Обозначим через [f_i] и [h_ij] целые части чисел f_i и h_ij.

Определение 1. Целой частью числа f_i называют наибольшее целое число, не превосходящее числа f_i.

Дробную часть чисел f_i и h_ij обозначим < f_i > < h_ij >, она определяется следующим образом:

Если f_i и хотя бы одно значение h_ij дробны, то с учётом введённых обозначений целых и дробных чисел дополнительное ограничение по целочисленности примет вид

Примечания. 1) Если f_i – дробное число, а все h_ij – целые числа, то задача линейного программирования не имеет целочисленного решения.

2) Ограничение целочисленности может быть наложено не на все переменные, а лишь на их часть. В этом случае задача является частично целочисленной.

Графический метод решения задач

При наличии в задаче линейного программирования двух переменных, а в системе ограничений – неравенств она может быть решена графическим путём.

В системе координат Х₁ОХ₂ находят область допустимых решений, строят и линию уровня. Перемещая линию уровня по направлению для задач на максимум, находим наиболее удалённую от начала координат точку и её координаты.

В том случае, когда координаты этой точки нецелочисленные, в области допустимых решений строят целочисленную решётку и находят на ней такие целые числа, которые удовлетворяют системе ограничений и при которых значение целевой функции наиболее близко к экстремальному целочисленному решению. Координаты такой вершины и являются целочисленным решением.

Аналогично решается задача на минимум.

Прогнозирование эффективного использования производственных площадей

Задача. Для улучшения финансового положения фирма приняла решение об увеличении выпуска конкурентоспособной продукции, для чего принято решение об установке в одном из цехов дополнительного оборудования, занимающего 19/3 м 2 площади. На приобретение дополнительного оборудования фирма выделила 10 усл. ед., при этом она может купить оборудование двух видов. Приобретение 1-го комплекта оборудования 1-го вида стоит 1,0 усл. ед., 2-го вида – 3 усл. ед. Приобретение одного комплекта оборудования 1-го вида позволяет увеличить выпуск продукции в смену на 2 шт., а одного комплекта оборудования 2-го вида – на 4 шт. Зная, что для установки одного комплекта оборудования 1-го вида требуется 2 м 2 площади, а для оборудования 2-го вида – 1 м 2 площади, определить такой набор дополнительного оборудования, который даёт возможность максимально увеличить выпуск продукции.

РЕШЕНИЕ. Составим математическую модель задачи. Предположим, что фирма приобретает х₁ комплектов дополнительного оборудования 1-го вида и х₂ комплектов оборудования 2-го вида. Математическая модель задачи будет иметь вид

Получим задачу целочисленного программирования, так как неизвестных только два, то решение задачи найдём графическим способом.

ОТВЕТ. Фирме следует приобрести один комплект оборудования 1-го вида и три комплекта оборудования 2-го вида, что обеспечит её при имеющихся ограничениях на производственные площади и денежные средства максимальное увеличение выпуска продукции, равное 14 усл.ед. в смену.

Решим эту же задачу методом Гомори.

Источник

Тема 5. Целочисленное программирование Постановка задачи

Значительная часть задач оптимального планирования по смыслу может иметь решения только в целых числах. Такие задачи связаны с определением количества единиц неделимой продукции, например, числа станков при загрузке оборудования, численности работников в структурных подразделениях предприятия и т.д.

Такие задачи решаются методами целочисленного программирования, где общая постановка задачи линейного программирования дополняется требованием о том, чтобы найденные переменные в оптимальном плане были целыми.

Если функция и ограничения в таких задачах линейны и на переменные задачи наложено условие целочисленности, то такие задачи называются задачами линейного целочисленного программирования.

Задача линейного целочисленного программирования формулируется следующим образом: найти такое решение (план) , при котором линейная функцияпринимает максимальное или минимальное значение при ограничениях

Если не на все переменные наложено условие целочисленности, то такие задачи называются частично целочисленными.

В настоящее время наиболее широкое применение находят два основных метода решения задач целочисленного программирования:

Методы отсечения используют оптимальные решения, найденные для задач линейного программирования, сужая область допустимых решений до целочисленных границ, т.е. отсекая нецелочисленные допустимые планы, получают решения задач целочисленного программирования.

Комбинаторные методы достигают решений задач целочисленного программирования, рассматривая возможные варианты целочисленных ограничений для задачи оптимизации.

Графическое решение задачи целочисленного линейного программирования

Рассмотрим случай, когда число неизвестных равно двум. Для решения задачи графическим методом прежде строят многоугольник решений без условия целочисленности. Условию целочисленности переменных удовлетворяют не все координаты точек области допустимых решений, поэтому область допустимых решений ослабленной задачи (без условия целочисленности) заменяется на выпуклый многоугольник, содержащий только допустимые точки с целочисленными координатами. Чтобы найти максимум или минимум целевой функции на выпуклой оболочке строят вектор градиент С(с₁, с₂). Передвигая прямую Z =c₁x₁+c₂x₂ в направлении вектора С, в результате чего находят точку, в которой целевая функция принимает оптимальное значение. Затем определяем координаты точки экстремума функции и вычисляем значение целевой функции в этой точке.

Пример. Найти максимальное значение целевой функции при заданных ограничениях:

Решение. Поскольку число неизвестных задачи равно двум, то решение данной задачи можно найти графически. Для этого построим многоугольник решений задачи без условия целочисленности.

Условию целочисленности удовлетворяют лишь 12 точек, отмеченных на рисунке. Чтобы найти точку, координаты которой определим решение исходной задачи, заменяя многоугольник ОАВС многоугольником OKEMNF, содержащий все допустимые точки с целочисленными координатами.

Для определения максимального значения целевой функции на многоугольнике OKEMNF построим вектор градиент С(2; 4) и прямую . Построенную прямую передвигаем в направлении вектора градиента до тех пор, пока она не пройдет через последнюю общую точку ее с этим многоугольником. Координаты полученной точки Е(1; 3) и являются оптимальным решением задачи, а значение целевой функции в ней F_max=14 является максимальным.

Источник

5.Лекция . Целочисленное программирование.

5. 1 Постановка задачи целочисленного программирования.

В ряде экономических задач, относящихся к задачам линейного программирования, элементы решения должны выражаться в целых числах. В этих задачах переменные означают количество единиц неделимой продукции.

Задача целочисленного программирования формулируется следующим образом:

Найти такое решение план Х=(х₁, х₂,…, х_n), при котором линейная функция принимает максимальное или минимальное значение при ограничениях

задача решается методами линейного программирования. В случае если переменные оптимального решения оказываются нецелочисленными, то, применяя методы отсечения или метод перебора целочисленных решений.

Понятия о методе ветвей и границ.

Метод ветвей и границ заключается в упорядоченном переборе вариантов и рассмотрении лишь тех из них, которые оказываются по определенным признакам перспективными, и отбрасывании бесперспективных вариантов.

Метод ветвей и границ состоит в следующем: множество допустимых решений (планов) некоторым способом разбивается на подмножества, каждое из которых этим же способом снова разбивается на подмножества. Процесс продолжается до тех пор. Пока не получено оптимальное целочисленное решение исходной задачи.

Название метода ветвей и границ исходит из того, что в процессе решения задача последовательно «ветвится», заменяясь более простыми. Процесс решения можно продолжать в виде дерева, цифры в узлах (вершинах) которого обозначают план решения задачи (искомые переменные).

5. 2 Графический метод решения задач целочисленного программирования.

При наличии в задаче линейного программирования двух переменных, а в системе ограничения – неравенств, она может быть решена графическим методом без требований целочисленных переменных.

Если оптимальное решение этой задачи является целочисленным, то оно и является оптимальным для исходной задачи.

Если же полученное оптимальное решение не целочисленное, то строится дополнительное линейное ограничение. Оно обладает следующими свойствами:

1. Оно должно быть линейным;
2. Должно отсекать найденный оптимальный не целочисленный план;
3. Не должно отсекать ни одного целочисленного плана.

1. Построить систему координат x₁0х₂ и выбрать масштаб.
2. Найти область допустимых решений (ОДР) системы ограничений задачи.
3. Построить целевую функцию, являющуюся линией уровня и на ней указать направление нормали.
4. Переместить линию целевой функции по направлению нормали через ОДР, чтобы она из секущей стала касательной к ОДР и проходила через наиболее удаленную от начала координат точку. Эта точка будет являться точкой экстремума, т.е. решением задачи.

1. Найти координаты, точки экстремума и значение целевой функции в ней. Если полученные значения не целочисленные, то перейти к следующему шагу.
2. Выделить у этих координат область с целочисленными значениями.
3. Определить новые координаты и построить граф.
4. Найти точки с целыми значениями искомых переменных, подставить в уравнение целевой функции и найти её значение. Максимальное из полученных значений целевой функции и будет решением задачи.

Источник