Обход в ширину графа python

Поиск в ширину (Breadth first search, BFS)

Обход означает посещение всех узлов графа. «Обход в ширину» или «Поиск в ширину» (Breadth first traversal or Breadth first Search) — это рекурсивный алгоритм поиска всех вершин графа или древовидной структуры данных. В этой статье вы познакомитесь с примерами алгоритма BFS, псевдокода BFS и кодом алгоритма «поиска в ширину» с реализацией в программах на C ++, C, Java и Python.

Алгоритм BFS

Цель алгоритма — пометить каждую вершину, как посещенную, избегая циклов.

Алгоритм работает следующим образом:

1. Начните с размещения любой вершины графа в конце очереди.
2. Возьмите передний элемент очереди и добавьте его в список посещенных.
3. Создайте список смежных узлов этой вершины. Добавьте те, которых нет в списке посещенных, в конец очереди.
4. Продолжайте повторять шаги 2 и 3, пока очередь не опустеет.

Граф может иметь две разные несвязанные части, поэтому, чтобы убедиться, что мы покрываем каждую вершину, мы также можем запустить алгоритм BFS на каждом узле.

Пример BFS

Давайте посмотрим, как алгоритм «поиска в ширину» работает на примере. Мы используем неориентированный граф с 5 вершинами.

Мы начнем с вершины 0, алгоритм BFS начинается с помещения его в список посещенных и размещения всех смежных вершин в стеке.

Затем мы посещаем элемент в начале очереди, то есть 1, и переходим к соседним узлам. Так как 0 уже был посещен, мы посещаем 2.

У вершины 2 есть соседняя не посещенная вершина 4, поэтому мы добавляем ее в конец очереди и посещаем 3, которая находится в начале очереди.

В очереди остается только 4, поскольку единственный соседний узел с 3, то есть 0, уже посещен. Мы посещаем вершину 4.

Поскольку очередь пуста, мы завершили обход в ширину графика.

BFS псевдокод

create a queue Q mark v as visited and put v into Q while Q is non-empty remove the head u of Q mark and enqueue all (unvisited) neighbours of u
 
Код BFS
 
Код для алгоритма «поиска в ширину» с примером показан ниже. Код был упрощен, поэтому мы можем сосредоточиться на алгоритме, а не на других деталях.
 
BFS в C
 
#include #include #define SIZE 40 struct queue < int items[SIZE]; int front; int rear; >; struct queue* createQueue(); void enqueue(struct queue* q, int); int dequeue(struct queue* q); void display(struct queue* q); int isEmpty(struct queue* q); void printQueue(struct queue* q); struct node < int vertex; struct node* next; >; struct node* createNode(int); struct Graph < int numVertices; struct node** adjLists; int* visited; >; struct Graph* createGraph(int vertices); void addEdge(struct Graph* graph, int src, int dest); void printGraph(struct Graph* graph); void bfs(struct Graph* graph, int startVertex); int main() < struct Graph* graph = createGraph(6); addEdge(graph, 0, 1); addEdge(graph, 0, 2); addEdge(graph, 1, 2); addEdge(graph, 1, 4); addEdge(graph, 1, 3); addEdge(graph, 2, 4); addEdge(graph, 3, 4); bfs(graph, 0); return 0; >void bfs(struct Graph* graph, int startVertex) < struct queue* q = createQueue(); graph->visited[startVertex] = 1; enqueue(q, startVertex); while(!isEmpty(q))< printQueue(q); int currentVertex = dequeue(q); printf("Visited %d\n", currentVertex); struct node* temp = graph->adjLists[currentVertex]; while(temp) < int adjVertex = temp->vertex; if(graph->visited[adjVertex] == 0)< graph->visited[adjVertex] = 1; enqueue(q, adjVertex); > temp = temp->next; > > > struct node* createNode(int v) < struct node* newNode = malloc(sizeof(struct node)); newNode->vertex = v; newNode->next = NULL; return newNode; > struct Graph* createGraph(int vertices) < struct Graph* graph = malloc(sizeof(struct Graph)); graph->numVertices = vertices; graph->adjLists = malloc(vertices * sizeof(struct node*)); graph->visited = malloc(vertices * sizeof(int)); int i; for (i = 0; i < vertices; i++) < graph->adjLists[i] = NULL; graph->visited[i] = 0; > return graph; > void addEdge(struct Graph* graph, int src, int dest) < // Add edge from src to dest struct node* newNode = createNode(dest); newNode->next = graph->adjLists[src]; graph->adjLists[src] = newNode; // Add edge from dest to src newNode = createNode(src); newNode->next = graph->adjLists[dest]; graph->adjLists[dest] = newNode; > struct queue* createQueue() < struct queue* q = malloc(sizeof(struct queue)); q->front = -1; q->rear = -1; return q; > int isEmpty(struct queue* q) < if(q->rear == -1) return 1; else return 0; > void enqueue(struct queue* q, int value)< if(q->rear == SIZE-1) printf("\nQueue is Full!!"); else < if(q->front == -1) q->front = 0; q->rear++; q->items[q->rear] = value; > > int dequeue(struct queue* q) < int item; if(isEmpty(q))< printf("Queue is empty"); item = -1; >else< item = q->items[q->front]; q->front++; if(q->front > q->rear)< printf("Resetting queue"); q->front = q->rear = -1; > > return item; > void printQueue(struct queue *q) < int i = q->front; if(isEmpty(q)) < printf("Queue is empty"); >else < printf("\nQueue contains \n"); for(i = q->front; i < q->rear + 1; i++) < printf("%d ", q->items[i]); > > >
 
BFS в C++
 
#include #include using namespace std; class Graph < int numVertices; list *adjLists; bool* visited; public: Graph(int vertices); void addEdge(int src, int dest); void BFS(int startVertex); >; Graph::Graph(int vertices) < numVertices = vertices; adjLists = new list[vertices]; >void Graph::addEdge(int src, int dest) < adjLists[src].push_back(dest); adjLists[dest].push_back(src); >void Graph::BFS(int startVertex) < visited = new bool[numVertices]; for(int i = 0; i < numVertices; i++) visited[i] = false; list queue; visited[startVertex] = true; queue.push_back(startVertex); list::iterator i; while(!queue.empty()) < int currVertex = queue.front(); cout > > > int main()
 
BFS Java код (Java code)
 
import java.io.*; import java.util.*; class Graph < private int numVertices; private LinkedListadjLists[]; private boolean visited[]; Graph(int v) < numVertices = v; visited = new boolean[numVertices]; adjLists = new LinkedList[numVertices]; for (int i=0; i i = adjLists[currVertex].listIterator(); while (i.hasNext()) < int adjVertex = i.next(); if (!visited[adjVertex]) < visited[adjVertex] = true; queue.add(adjVertex); >> > > public static void main(String args[]) < Graph g = new Graph(4); g.addEdge(0, 1); g.addEdge(0, 2); g.addEdge(1, 2); g.addEdge(2, 0); g.addEdge(2, 3); g.addEdge(3, 3); System.out.println("Following is Breadth First Traversal "+ "(starting from vertex 2)"); g.BFS(2); >>
 
BFS в Python
 
import collections def bfs(graph, root): visited, queue = set(), collections.deque([root]) visited.add(root) while queue: vertex = queue.popleft() for neighbour in graph[vertex]: if neighbour not in visited: visited.add(neighbour) queue.append(neighbour) if __name__ == '__main__': graph = breadth_first_search(graph, 0)
 
 
Рекомендуем хостинг TIMEWEB
 
Стабильный хостинг, на котором располагается социальная сеть EVILEG. Для проектов на Django рекомендуем VDS хостинг.
 
Рекомендуемые статьи по этой тематике
 
По статье задано0 вопрос(ов) 
 
Вам это нравится? Поделитесь в социальных сетях!
 
Источник
 
Breadth First Search in Python (with Code) | BFS Algorithm
 
 
Breadth-first search and Depth-first search in python are algorithms used to traverse a graph or a tree. They are two of the most important topics that any new python programmer should definitely learn about. Here we will study what breadth-first search in python is, understand how it works with its algorithm, implementation with python code, and the corresponding output to it. Also, we will find out the application and uses of breadth-first search in the real world.
 
What is Breadth-First Search?
 
As discussed earlier, Breadth-First Search (BFS) is an algorithm used for traversing graphs or trees. Traversing means visiting each node of the graph. Breadth-First Search is a recursive algorithm to search all the vertices of a graph or a tree. BFS in python can be implemented by using data structures like a dictionary and lists. Breadth-First Search in tree and graph is almost the same. The only difference is that the graph may contain cycles, so we may traverse to the same node again.
 
BFS Algorithm
 
Before learning the python code for Breadth-First and its output, let us go through the algorithm it follows for the same. We can take the example of Rubik’s Cube for the instance. Rubik’s Cube is seen as searching for a path to convert it from a full mess of colors to a single color. So comparing the Rubik’s Cube to the graph, we can say that the possible state of the cube is corresponding to the nodes of the graph and the possible actions of the cube is corresponding to the edges of the graph.
 
As breadth-first search is the process of traversing each node of the graph, a standard BFS algorithm traverses each vertex of the graph into two parts: 1) Visited 2) Not Visited. So, the purpose of the algorithm is to visit all the vertex while avoiding cycles.
 
BFS starts from a node, then it checks all the nodes at distance one from the beginning node, then it checks all the nodes at distance two, and so on. So as to recollect the nodes to be visited, BFS uses a queue.
 
The steps of the algorithm work as follow:
 
 
Start by putting any one of the graph’s vertices at the back of the queue.
 
Now take the front item of the queue and add it to the visited list.
 
Create a list of that vertex's adjacent nodes. Add those which are not within the visited list to the rear of the queue.
 
Keep continuing steps two and three till the queue is empty.
 
 
Many times, a graph may contain two different disconnected parts and therefore to make sure that we have visited every vertex, we can also run the BFS algorithm at every node.
 
BFS pseudocode
 
The pseudocode for BFS in python goes as below:
 
 create a queue Q 
 
 mark v as visited and put v into Q 
 
 while Q is non-empty 
 
 remove the head u of Q 
 
 mark and enqueue all (unvisited) neighbors of u 
 
BFS implementation in Python (Source Code)
 
Now, we will see how the source code of the program for implementing breadth first search in python.
 
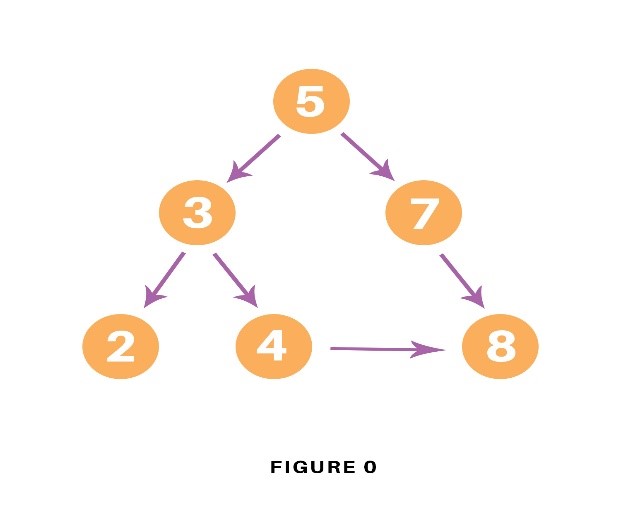
Consider the following graph which is implemented in the code below:
 
 
graph = < '5' : ['3','7'], '3' : ['2', '4'], '7' : ['8'], '2' : [], '4' : ['8'], '8' : [] > visited = [] # List for visited nodes. queue = [] #Initialize a queue def bfs(visited, graph, node): #function for BFS visited.append(node) queue.append(node) while queue: # Creating loop to visit each node m = queue.pop(0) print (m, end = " ") for neighbour in graph[m]: if neighbour not in visited: visited.append(neighbour) queue.append(neighbour) # Driver Code print("Following is the Breadth-First Search") bfs(visited, graph, '5') # function calling 
 
In the above code, first, we will create the graph for which we will use the breadth-first search. After creation, we will create two lists, one to store the visited node of the graph and another one for storing the nodes in the queue.
 
After the above process, we will declare a function with the parameters as visited nodes, the graph itself and the node respectively. And inside a function, we will keep appending the visited and queue lists.
 
Then we will run the while loop for the queue for visiting the nodes and then will remove the same node and print it as it is visited.
 
At last, we will run the for loop to check the not visited nodes and then append the same from the visited and queue list.
 
As the driver code, we will call the user to define the bfs function with the first node we wish to visit.
 
Output
 
The output of the above code will be as follow:
 
Following is the Breadth-First Search 
5 3 7 2 4 8
 
Example
 
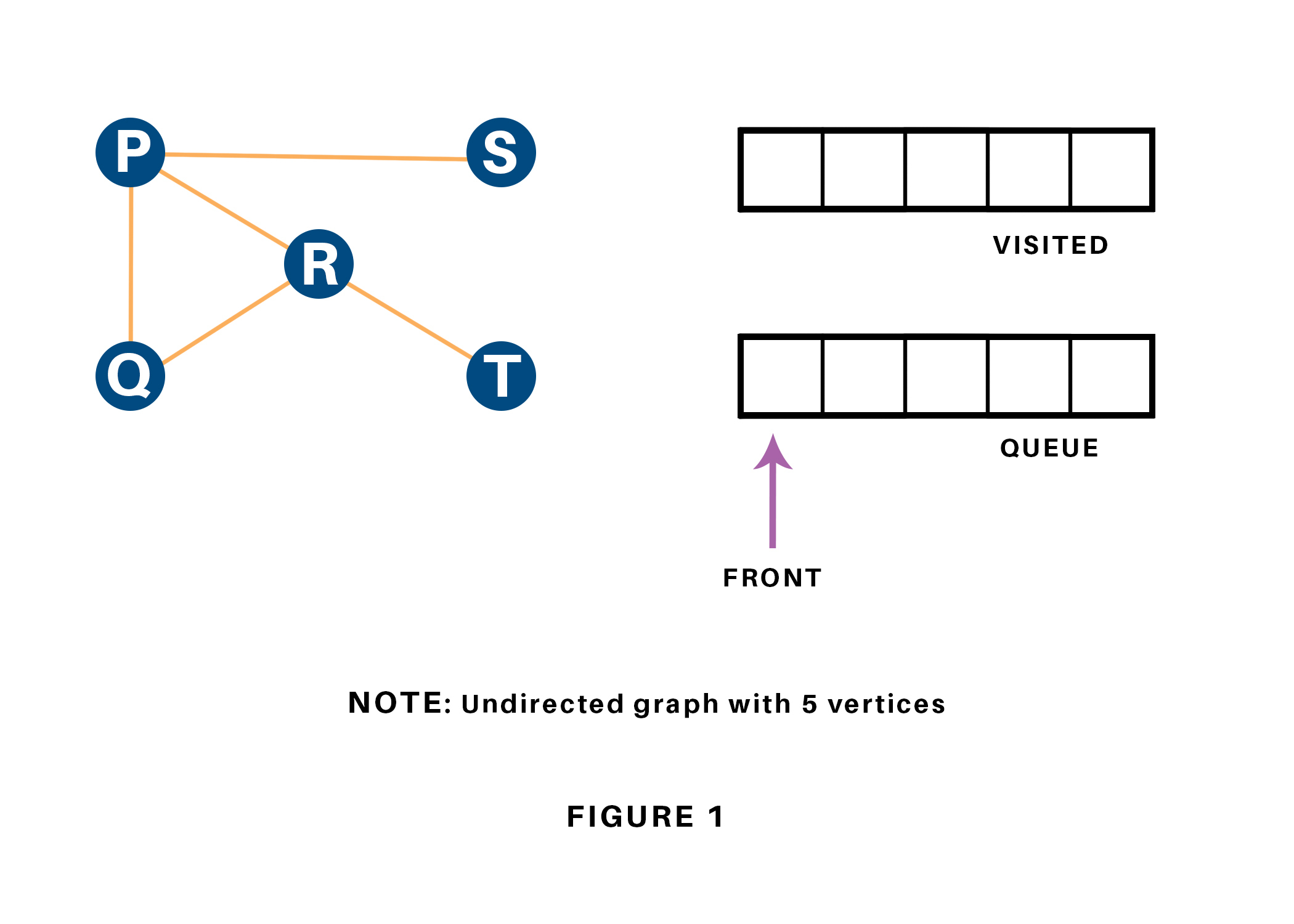
Let us see how this algorithm works with an example. Here, we will use an undirected graph with 5 vertices.
 
 
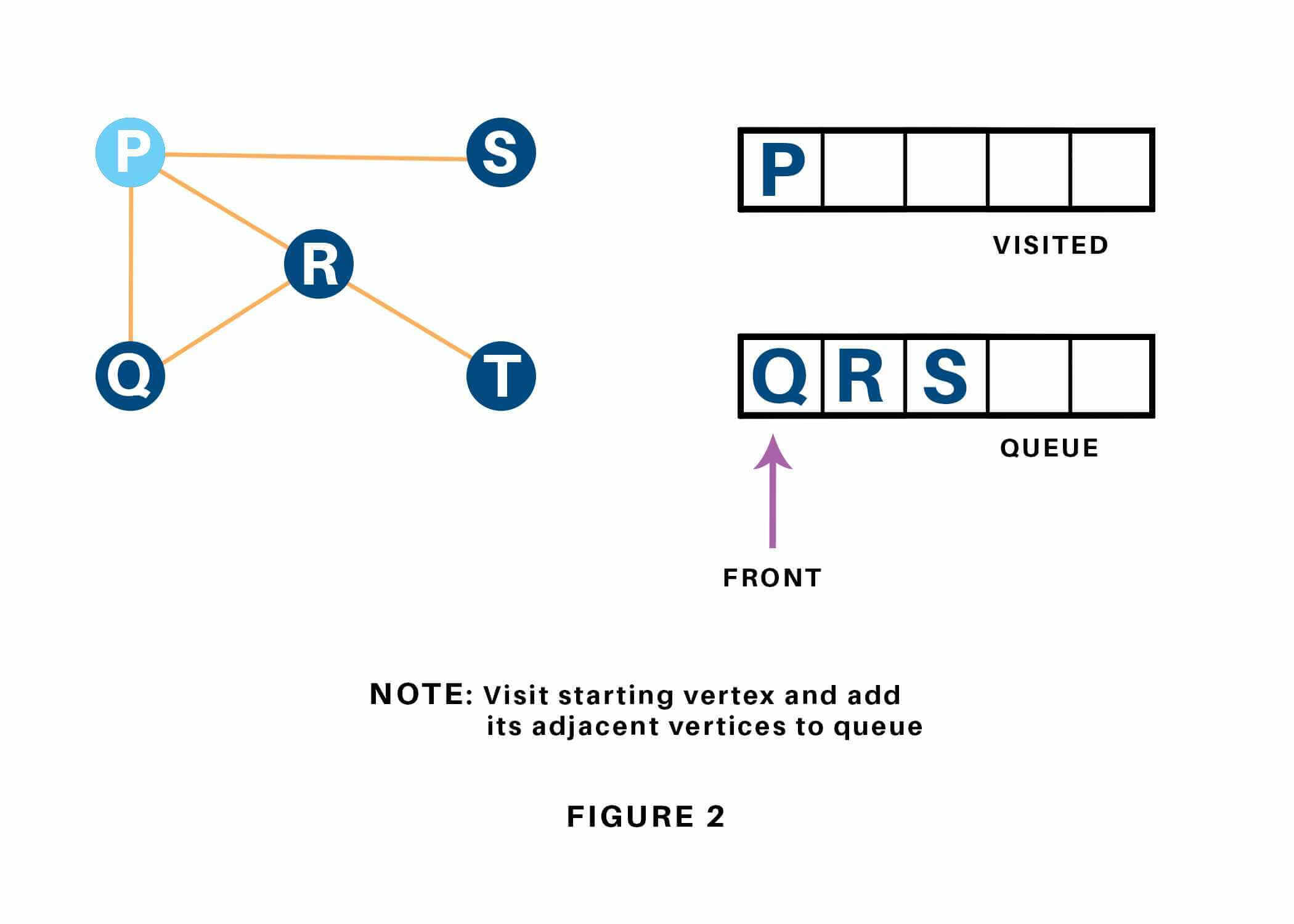
We begin from the vertex P, the BFS algorithmic program starts by putting it within the Visited list and puts all its adjacent vertices within the stack.
 
 
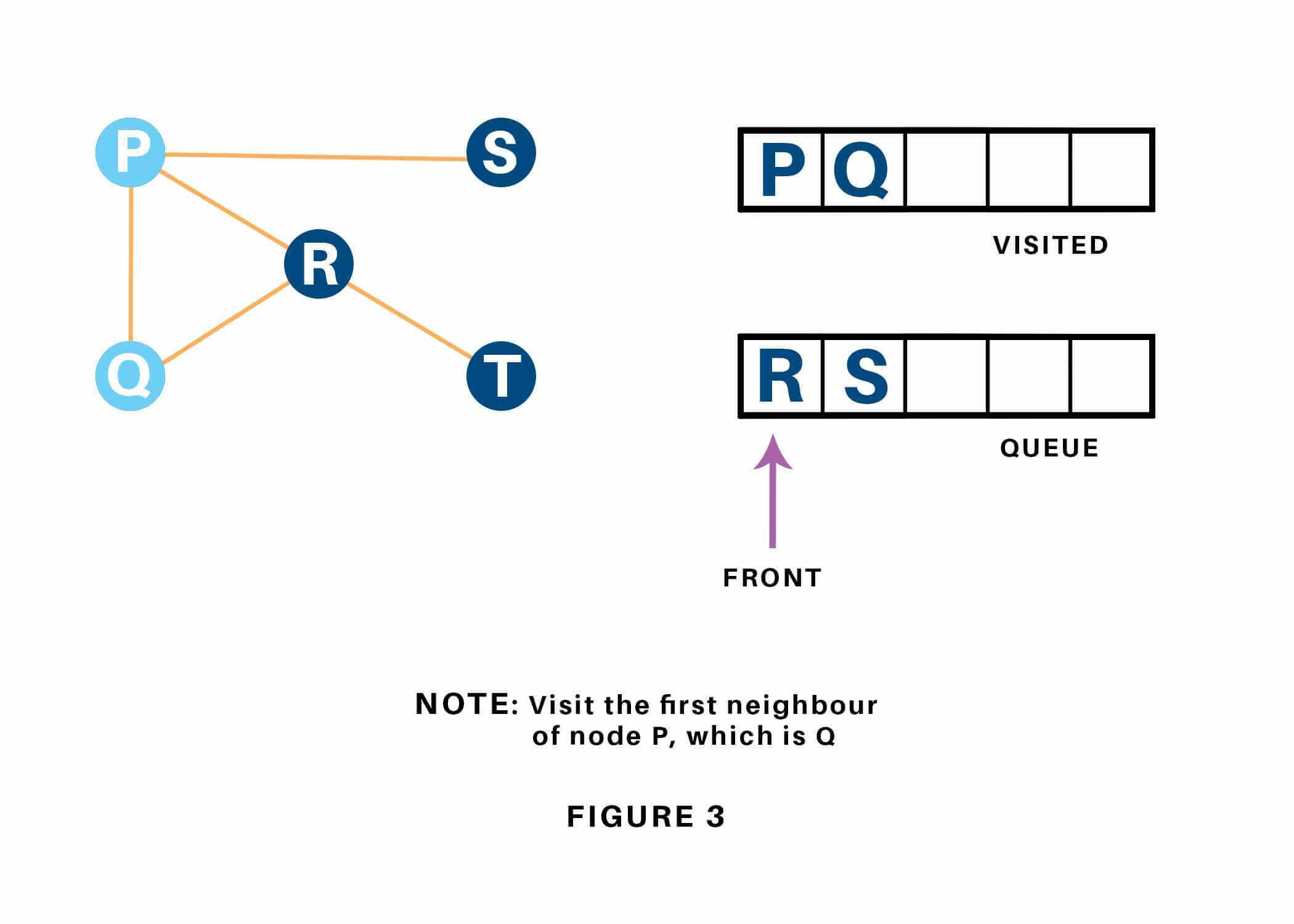
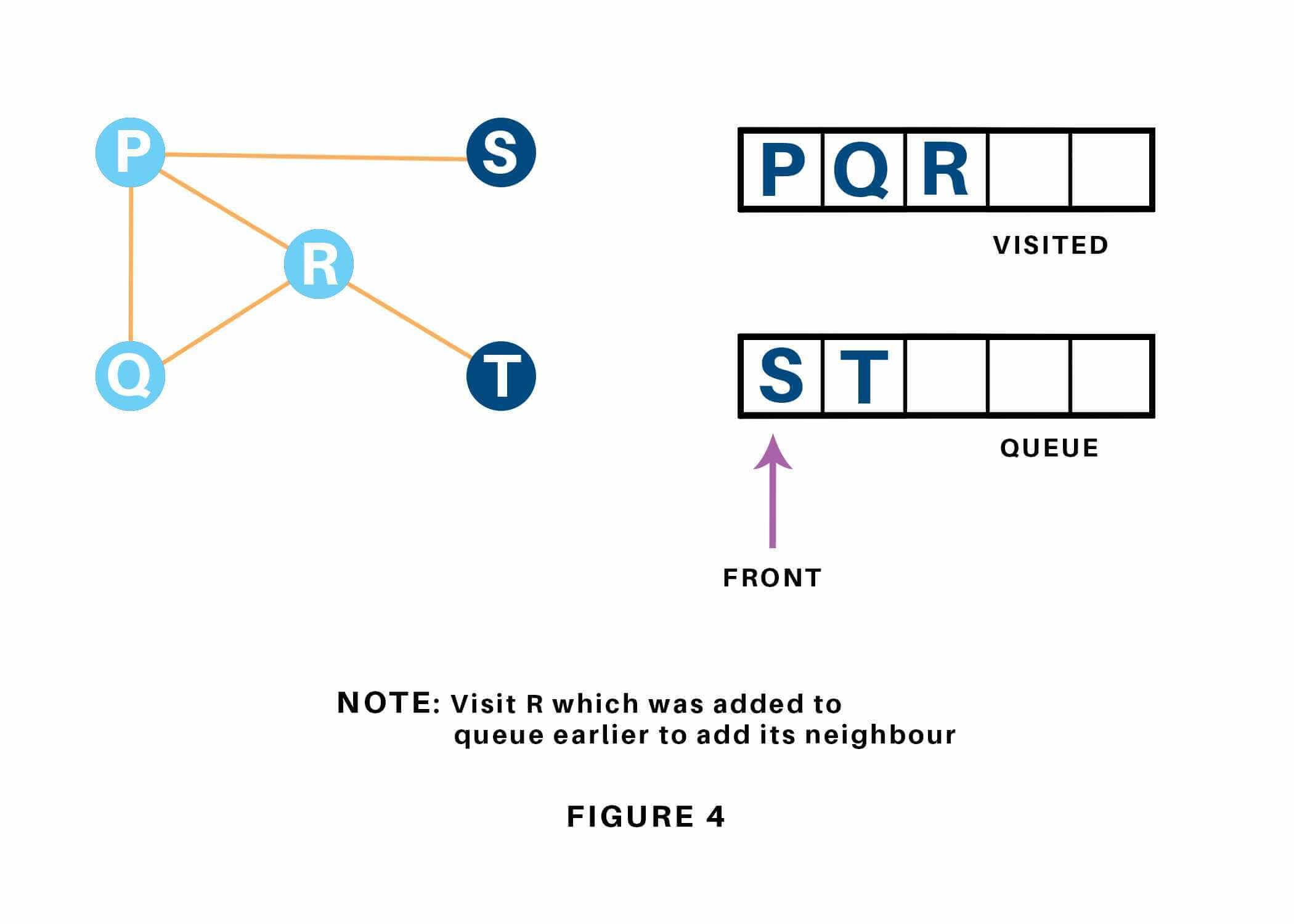
Next, we have a tendency to visit the part at the front of the queue i.e. Q and visit its adjacent nodes. Since P has already been visited, we have a tendency to visit R instead.
 
 
Vertex R has an unvisited adjacent vertex in T, thus we have a tendency to add that to the rear of the queue and visit S, which is at the front of the queue.
 
 
 
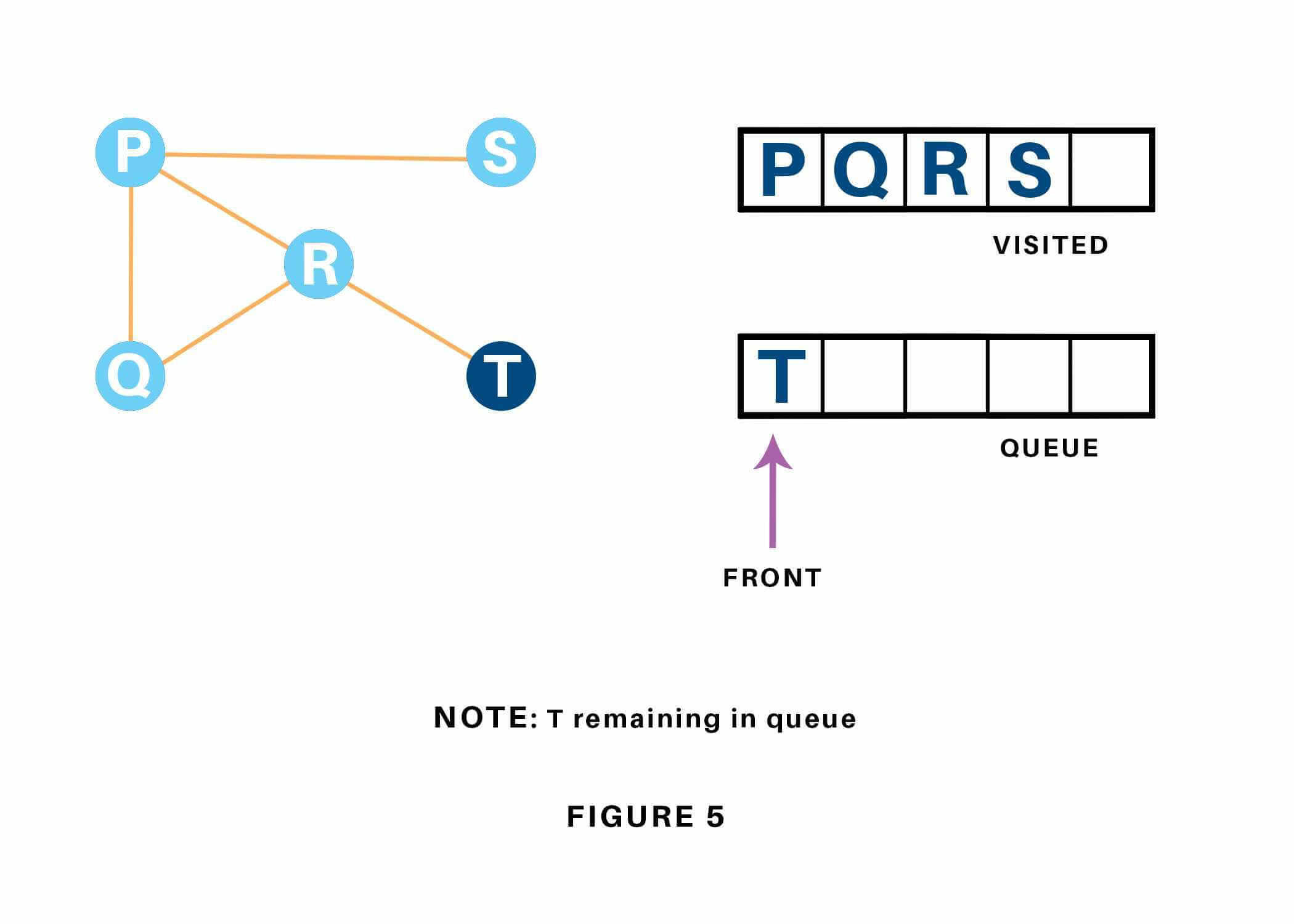
Now, only T remains within the queue since the only adjacent node of S i.e. P is already visited. We have a tendency to visit it.
 
 
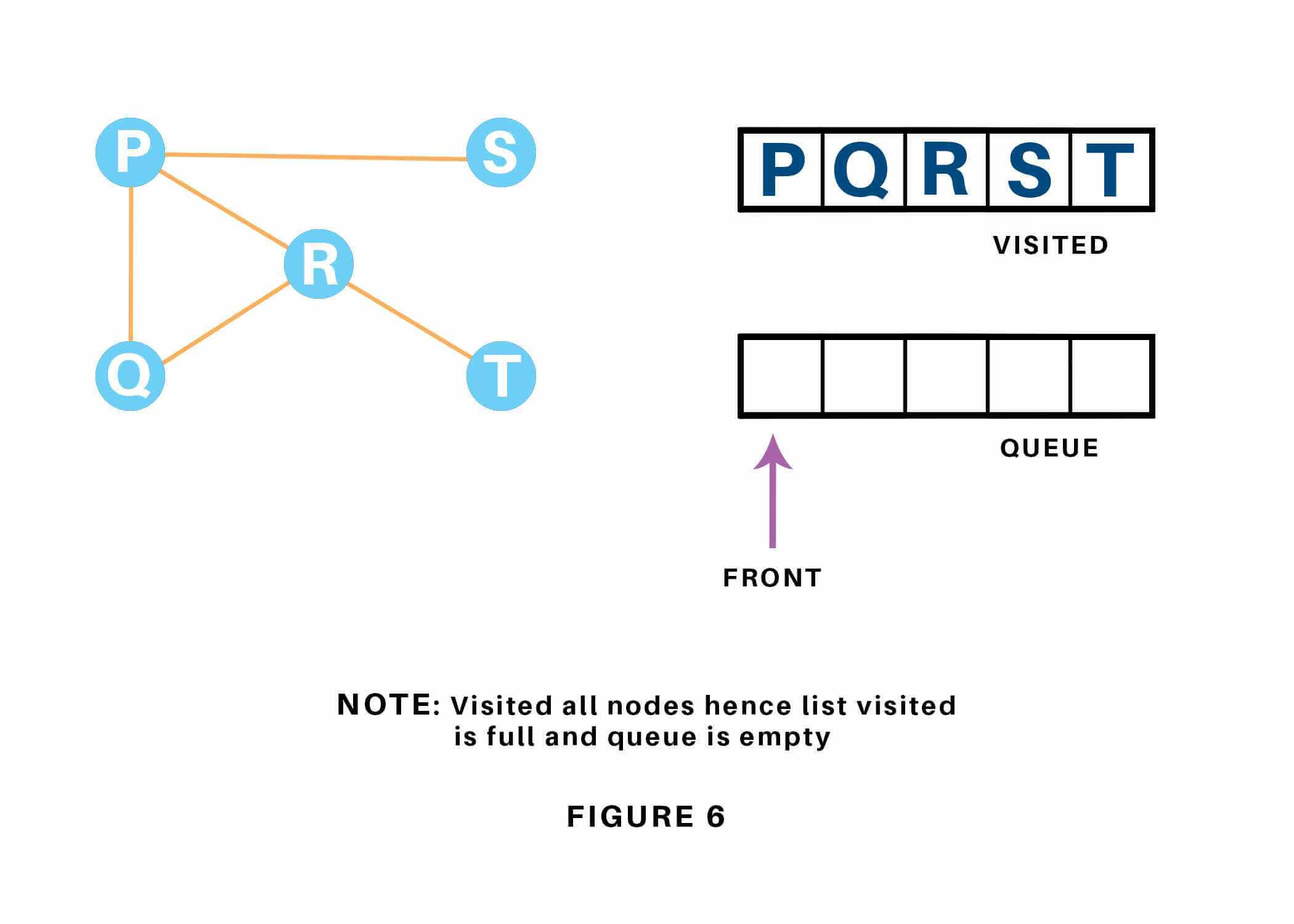
Since the queue is empty, we've completed the Traversal of the graph.
 
Time Complexity
 
The time complexity of the Breadth first Search algorithm is in the form of O(V+E), where V is the representation of the number of nodes and E is the number of edges.
 
Also, the space complexity of the BFS algorithm is O(V).
 
Applications
 
Breadth-first Search Algorithm has a wide range of applications in the real-world. Some of them are as discussed below:
 
 
In GPS navigation, it helps in finding the shortest path available from one point to another.
 
In pathfinding algorithms
 
Cycle detection in an undirected graph
 
In minimum spanning tree
 
To build index by search index
 
In Ford-Fulkerson algorithm to find maximum flow in a network.
 
 
Conclusion
 
If you have a good understanding of core python concepts and with the help of what you read today, you can now easily implement breadth first search in python. I hope this article clearly explained how this algorithm works. If you need help with Python homework, contact our experts now!
 
Источник
 
Читайте также:  Running new thread java