Решение задач линейного программирования
Назначение сервиса . Онлайн-калькулятор предназначен для решения задач линейного программирования симплексным методом путем перехода к КЗЛП и СЗЛП . При этом задача на минимум целевой функции сводятся к задаче на поиск максимума через преобразование целевой функции F*(X) = -F(X) . Также имеется возможность составить двойственную задачу.
- Переход к КЗЛП. Любая ЗЛП вида ax ≤ b , ax ≥ b , ax = b ( F(X) → extr ) сводится к виду ax = b , F(X) → max ;
- Переход к СЗЛП. КЗЛП вида ax = b сводится к виду ax ≤ b , F(X) → max ;
- Решение симплексным методом;
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Инструкция . Выберите количество переменных и количество строк (количество ограничений). Полученное решение сохраняется в файле Word .
Переход от задачи минимизации целевой функции к задаче максимизации
Задача минимизации целевой функции F(X) легко может быть сведена к задаче максимизации функции F*(X) при тех же ограничениях путем введения функции: F*(X) = -F(X) . Обе задачи имеют одно и то же решение X*, и при этом min(F(X)) = -max(F*(X)) .
Проиллюстрируем этот факт графически:
| F(x) → min | F(x) → max |
Для оптимизации функции цели используем следующие понятия и методы.
Опорный план – план с определёнными через свободные базисными переменными.
Базисный план – опорный план с нулевыми базисными переменными.
Оптимальный план – базисный план, удовлетворяющий оптимальной функции цели (ФЦ).
Ведущий (разрешающий) элемент – коэффициент свободной неизвестной, которая становится базисной, а сам коэффициент преобразуется в единицу.
Направляющая строка – строка ведущего элемента, в которой расположена с единичным коэффициентом базисная неизвестная, исключаемая при преобразовании (строка с минимальным предельным коэффициентом, см. далее).
Направляющий столбец – столбец ведущего элемента, свободная неизвестная которого переводится в базисную (столбец с максимальной выгодой, см. далее).
Переменные x1, …, xm, входящие с единичными коэффициентами только в одно уравнение системы, с нулевыми – в остальные, называются базисными или зависимыми. В канонической системе каждому уравнению соответствует ровно одна базисная переменная. Переход осуществляется с помощью метода Гаусса–Жордана. Основная идея этого метода состоит в сведении системы m уравнений с n неизвестными к каноническому виду при помощи элементарных операций над строками.
Остальные n-m переменных (xm+1,…, xn) называются небазисными или независимыми переменными.
Базисное решение называется допустимым базисным решением, если значения входящих в него базисных переменных xj≥0, что эквивалентно условию неотрицательности bj≥0.
Допустимое базисное решение является угловой точкой допустимого множества S задачи линейного программирования и называется иногда опорным планом.
Если среди неотрицательных чисел bj есть равные нулю, то допустимое базисное решение называется вырожденным (вырожденной угловой точкой) и соответствующая задача линейного программирования называется вырожденной.
Пример №1 . Свести задачу линейного программирования к стандартной ЗЛП.
F(X) = x1 + 2x2 — 2x3 → min при ограничениях:
4x1 + 3x2 — x3≤10
— 2x2 + 5x3≥3
x1 + 2x3=9
Для приведения ЗЛП к канонической форме необходимо:
1. Поменять знак у целевой функции. Сведем задачу F(X) → min к задаче F(X) → max. Для этого умножаем F(X) на (-1). В первом неравенстве смысла (≤) вводим базисную переменную x4; во втором неравенстве смысла (≥) вводим базисную переменную x5 со знаком минус.
4x1 + 3x2-1x3 + 1x4 + 0x5 = 10
0x1-2x2 + 5x3 + 0x4-1x5 = 3
1x1 + 0x2 + 2x3 + 0x4 + 0x5 = 9
F(X) = — x1 — 2x2 + 2x3
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:
| 4 | 3 | -1 | 1 | 0 | 10 |
| 0 | -2 | 5 | 0 | -1 | 3 |
| 1 | 0 | 2 | 0 | 0 | 9 |
Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x4.
2. В качестве базовой переменной выбираем x2.
Разрешающий элемент РЭ=-2. Строка, соответствующая переменной x2, получена в результате деления всех элементов строки x2 на разрешающий элемент РЭ=-2. На месте разрешающего элемента получаем 1. В остальных клетках столбца x2 записываем нули. Все остальные элементы определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:
| 4-(0 • 3):-2 | 3-(-2 • 3):-2 | -1-(5 • 3):-2 | 1-(0 • 3):-2 | 0-(-1 • 3):-2 | 10-(3 • 3):-2 |
| 0 : -2 | -2 : -2 | 5 : -2 | 0 : -2 | -1 : -2 | 3 : -2 |
| 1-(0 • 0):-2 | 0-(-2 • 0):-2 | 2-(5 • 0):-2 | 0-(0 • 0):-2 | 0-(-1 • 0):-2 | 9-(3 • 0):-2 |
Получаем новую матрицу:
| 4 | 0 | 6 1 /2 | 1 | -1 1 /2 | 14 1 /2 |
| 0 | 1 | -2 1 /2 | 0 | 1 /2 | -1 1 /2 |
| 1 | 0 | 2 | 0 | 0 | 9 |
3. В качестве базовой переменной выбираем x3.
Разрешающий элемент РЭ=2. Строка, соответствующая переменной x3, получена в результате деления всех элементов строки x3 на разрешающий элемент РЭ=2. На месте разрешающего элемента получаем 1. В остальных клетках столбца x3 записываем нули. Все остальные элементы определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:
| 4-(1 • 6 1 /2):2 | 0-(0 • 6 1 /2):2 | 6 1 /2-(2 • 6 1 /2):2 | 1-(0 • 6 1 /2):2 | -1 1 /2-(0 • 6 1 /2):2 | 14 1 /2-(9 • 6 1 /2):2 |
| 0-(1 • -2 1 /2):2 | 1-(0 • -2 1 /2):2 | -2 1 /2-(2 • -2 1 /2):2 | 0-(0 • -2 1 /2):2 | 1 /2-(0 • -2 1 /2):2 | -1 1 /2-(9 • -2 1 /2):2 |
| 1 : 2 | 0 : 2 | 2 : 2 | 0 : 2 | 0 : 2 | 9 : 2 |
Получаем новую матрицу:
| 3 /4 | 0 | 0 | 1 | -1 1 /2 | -14 3 /4 |
| 1 1 /4 | 1 | 0 | 0 | 1 /2 | 9 3 /4 |
| 1 /2 | 0 | 1 | 0 | 0 | 4 1 /2 |
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (4,2,3).
Соответствующие уравнения имеют вид:
3 /4x1 + x4 — 1 1 /2x5 = -14 3 /4
1 1 /4x1 + x2 + 1 /2x5 = 9 3 /4
1 /2x1 + x3 = 4 1 /2
Выразим базисные переменные через остальные:
x4 = — 3 /4x1 + 1 1 /2x5-14 3 /4
x2 = — 1 1 /4x1 — 1 /2x5+9 3 /4
x3 = — 1 /2x1+4 1 /2
Подставим их в целевую функцию:
F(X) = — x1 — 2(- 1 1 /4x1 — 1 /2x5+9 3 /4) + 2(- 1 /2x1+4 1 /2)
или
F(X) = 1 /2x1 + x5-10 1 /2 → max
Система неравенств:
— 3 /4x1 + 1 1 /2x5-14 3 /4 ≥ 0
— 1 1 /4x1 — 1 /2x5+9 3 /4 ≥ 0
— 1 /2x1+4 1 /2 ≥ 0
Приводим систему неравенств к следующему виду:
3 /4x1 — 1 1 /2x5 ≤ -14 3 /4
1 1 /4x1 + 1 /2x5 ≤ 9 3 /4
1 /2x1 ≤ 4 1 /2
F(X) = 1 /2x1 + x5-10 1 /2 → max
Упростим систему.
3 /4x1 — 1 1 /2x2 ≤ -14 3 /4
1 1 /4x1 + 1 /2x2 ≤ 9 3 /4
1 /2x1 ≤ 4 1 /2
F(X) = 1 /2x1 + x2-10 1 /2 → max
6.1.2. Метод исключения переменных Пусть дана задача линейного программирования в канонической форме
f(x) = ,
аij xj = bi , i :m, (6.8)
xj ≥ 0, j = 1:n,
где число переменных на два больше числа ограничений − равенств, т.е. n —m= 2, причем ранг матрицыА =m. Тогда две переменные в указанной системе уравнений, скажемх1их2, являются свободными, т.е. через них можно выразить все остальные переменные:
, (6.9)
где − некоторые числа. Подставляя эти выражения в целевую функцию, получаем
где γ1, γ2, δ − некоторые числа.
Рассмотрим задачу линейного программирования с двумя переменными:
Используя геометрические построения, находим ее решение (). Подставляя эти числа в (6.9), (6.10), получаем решение и значение исходной задачи (6.8).
Пример6.2.Используя графический метод, найти решение
Рис. 6.2. Допустимое множество задачи 6.2
Решение. Изобразим на плоскости (х1, х2) допустимое множество данной задачи (многоугольник ABCDE, рис. 6.2) и одну из линий уровня —х1 -2х2 = — 3 целевой функции х. Направление убывания (x) указывает вектор l = (1,2). Совершая параллельный перенос линии уровня вдоль направления l, находим ее крайнее положение. В этом положении прямая —х1 — 2х2 = — 3 проходит через сторону CD полиэдра ABCDE. Таким образом, все точки отрезка CD являются точками минимума функции х на множестве X. Так как концы C и D этого отрезка имеют координаты (1,3) и (3,2) соответственно, то любая точка минимума функции х представима в виде
где . Минимальное значение целевой функции * =(х*) = –7.

Рис. 6.3. Неограниченное многоугольное множество
Решение. Допустимое множество этой задачи представляет собой неограниченное многоугольное множество (рис. 6.3). Функцияf(x) убывает в направленииl= (1,2). При параллельном переносе линии уровнявдоль направленияlона всегда пересекает множествоХ, а целевая функцияf(x) неограниченно убывает. Поэтому рассмотренная задача не имеет решений.
Пример 6.4.Найти максимальное значение функции
при условиях:
Решение.В отличие от рассмотренных выше задач в исходной задаче ограничения заданы в виде уравнений. При этом число неизвестных равно пяти. Поэтому данную задачу следует свести к задаче, в которой число неизвестных было бы равно двум. В рассматриваемом случае это можно сделать путем перехода от исходной задачи, записанной в форме основной, к задаче, записанной в форме стандартной.
Из целевой функции исходной задачи исключаем переменные x3, x4, x5 с помощью подстановки их значений из соответствующих уравнений системы ограничений. Получаем постановку задачи в стандартной форме:
f(x) = 2x1 +3x2,
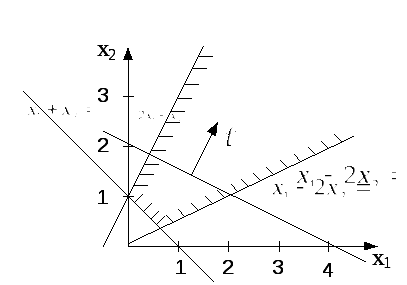
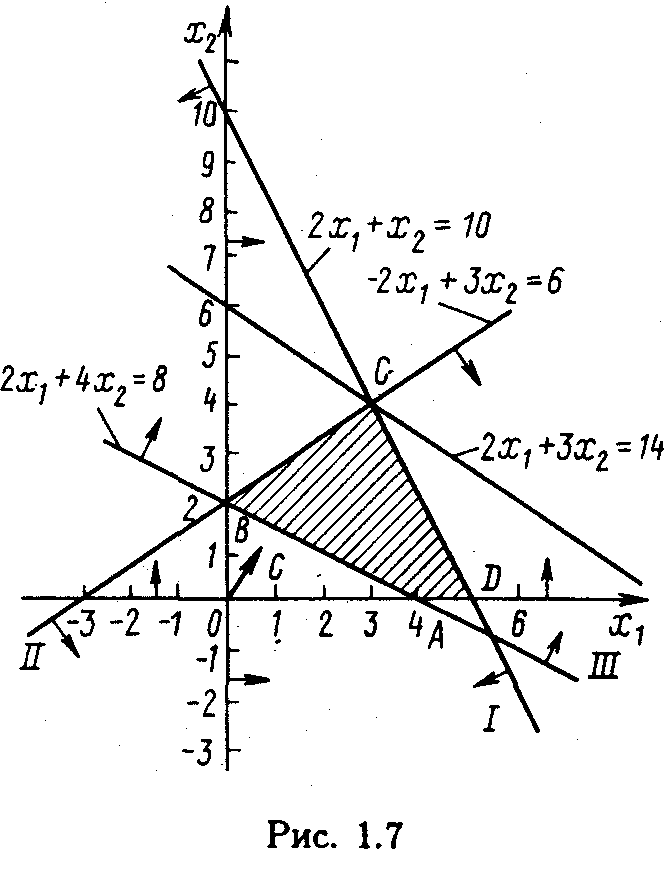
Рис. 6.4. Многоугольник решений
Построим многоугольник решений полученной задачи (рис. 6.4). Как видно из рис. 6.4., максимальное значение целевая функция задачи принимает в точке С пересечения прямыхIиII.Вдоль каждой из граничных прямых значение одной из переменных, исключенной при переходе к соответствующему неравенству, равно нулю. Поэтому в каждой из вершин полученного многоугольника решений последней задачи по крайней мере две переменные исходной задачи принимают нулевые значения. Так, в точкеС имеемx3 = 0 иx4 = 0. Подставляя эти значения в первое и второе уравнения системы ограничений исходной задачи, получаем систему двух уравнений
решая которую, находим x1* =3,x2* = 4.
Подставляя найденные значения x1иx2в третье уравнение системы ограничений исходной задачи, определяем значение переменнойx5 равное 14.
Следовательно, оптимальным планом рассматриваемой задачи является x* = (3; 4; 0; 0; 14). При этом плане значение целевой функции есть max = 18.
Задача 6
Используя метод исключения переменных и геометрические построения, найти решение задачи Линейного Программирования: 
- Из третьего ограничения
можно выразить
:
- Подставим выражение для
в первое ограничение
:
- Подставим выражение для
во второе ограничение
:
- Таким образом, после применения метода исключения переменных от исходной задачи перейдем к задаче вида:

- Необходимо на плоскости построить прямые, соответствующие заданным неравенствам.
Прямая, соответствующая неравенству 




- Строим на плоскости прямые, соответствующие данным прямым.
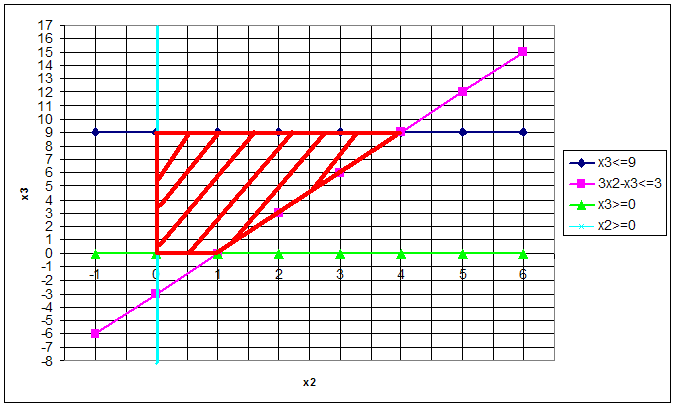
- Определяем ОДЗ (Область допустимых значений) данной системы неравенств. ОДЗ- это многогранник, ограниченный заданной системой неравенств, каждая точка которого удовлетворяет всем неравенствам ( условиям).

- Строим вектор целевой функции
. Для этого необходимо построить линию уровня целевой функции, где
, а затем определить в какую сторону целевая функция возрастает.
Линия уровня целевой функции 









- Мысленно передвигая параллельно линию уровня целевой функции вверх, нужно определить крайнюю точку ОДЗ, которую пересекают линии уровня целевой функции.
Для данной ОДЗ целевая функция 


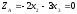











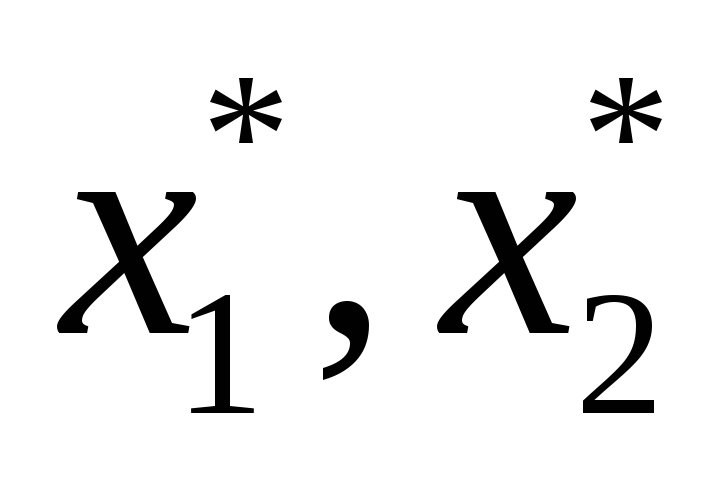







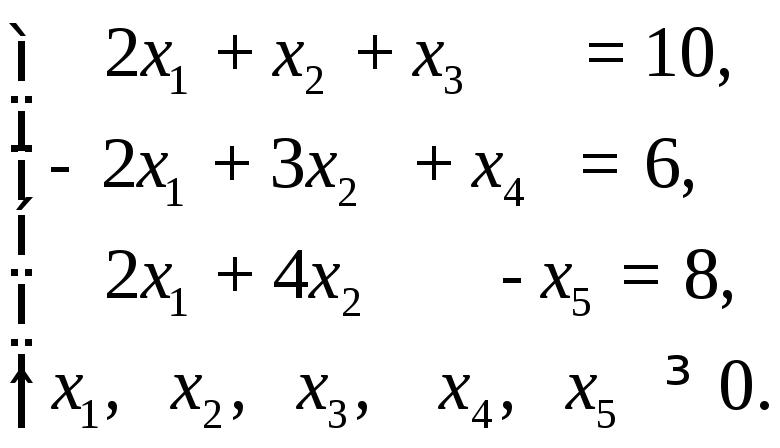



 можно выразить
можно выразить :
:
 в первое ограничение
в первое ограничение :
:
 во второе ограничение
во второе ограничение :
: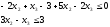


 . Для этого необходимо построить линию уровня целевой функции, где
. Для этого необходимо построить линию уровня целевой функции, где , а затем определить в какую сторону целевая функция возрастает.
, а затем определить в какую сторону целевая функция возрастает.
