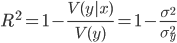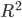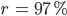Multi linear regression python

Machine Learning — Multiple Regression

Multiple regression is like linear regression, but with more than one independent value, meaning that we try to predict a value based on two or more variables.

Take a look at the data set below, it contains some information about cars.

Toyota	Aygo	1000	790	99
Mitsubishi	Space Star	1200	1160	95
Skoda	Citigo	1000	929	95
Fiat	500	900	865	90
Mini	Cooper	1500	1140	105
VW	Up!	1000	929	105
Skoda	Fabia	1400	1109	90
Mercedes	A-Class	1500	1365	92
Ford	Fiesta	1500	1112	98
Audi	A1	1600	1150	99
Hyundai	I20	1100	980	99
Suzuki	Swift	1300	990	101
Ford	Fiesta	1000	1112	99
Honda	Civic	1600	1252	94
Hundai	I30	1600	1326	97
Opel	Astra	1600	1330	97
BMW	1	1600	1365	99
Mazda	3	2200	1280	104
Skoda	Rapid	1600	1119	104
Ford	Focus	2000	1328	105
Ford	Mondeo	1600	1584	94
Opel	Insignia	2000	1428	99
Mercedes	C-Class	2100	1365	99
Skoda	Octavia	1600	1415	99
Volvo	S60	2000	1415	99
Mercedes	CLA	1500	1465	102
Audi	A4	2000	1490	104
Audi	A6	2000	1725	114
Volvo	V70	1600	1523	109
BMW	5	2000	1705	114
Mercedes	E-Class	2100	1605	115
Volvo	XC70	2000	1746	117
Ford	B-Max	1600	1235	104
BMW	2	1600	1390	108
Opel	Zafira	1600	1405	109
Mercedes	SLK	2500	1395	120

We can predict the CO2 emission of a car based on the size of the engine, but with multiple regression we can throw in more variables, like the weight of the car, to make the prediction more accurate.

How Does it Work?

In Python we have modules that will do the work for us. Start by importing the Pandas module.

Learn about the Pandas module in our Pandas Tutorial.

The Pandas module allows us to read csv files and return a DataFrame object.

The file is meant for testing purposes only, you can download it here: data.csv

Then make a list of the independent values and call this variable X .

Put the dependent values in a variable called y .

X = df[[‘Weight’, ‘Volume’]]
y = df[‘CO2’]

Tip: It is common to name the list of independent values with a upper case X, and the list of dependent values with a lower case y.

We will use some methods from the sklearn module, so we will have to import that module as well:

from sklearn import linear_model

From the sklearn module we will use the LinearRegression() method to create a linear regression object.

This object has a method called fit() that takes the independent and dependent values as parameters and fills the regression object with data that describes the relationship:

regr = linear_model.LinearRegression()
regr.fit(X, y)

Now we have a regression object that are ready to predict CO2 values based on a car’s weight and volume:

#predict the CO2 emission of a car where the weight is 2300kg, and the volume is 1300cm 3 :
predictedCO2 = regr.predict([[2300, 1300]])

Example

See the whole example in action:

import pandas
from sklearn import linear_model

X = df[[‘Weight’, ‘Volume’]]y = df[‘CO2’]

regr = linear_model.LinearRegression()
regr.fit(X, y)

#predict the CO2 emission of a car where the weight is 2300kg, and the volume is 1300cm 3 :
predictedCO2 = regr.predict([[2300, 1300]])

Result:

We have predicted that a car with 1.3 liter engine, and a weight of 2300 kg, will release approximately 107 grams of CO2 for every kilometer it drives.

Coefficient

The coefficient is a factor that describes the relationship with an unknown variable.

Example: if x is a variable, then 2x is x two times. x is the unknown variable, and the number 2 is the coefficient.

In this case, we can ask for the coefficient value of weight against CO2, and for volume against CO2. The answer(s) we get tells us what would happen if we increase, or decrease, one of the independent values.

Example

Print the coefficient values of the regression object:

import pandas
from sklearn import linear_model

X = df[[‘Weight’, ‘Volume’]]y = df[‘CO2’]

regr = linear_model.LinearRegression()
regr.fit(X, y)

Result:

Result Explained

The result array represents the coefficient values of weight and volume.

Weight: 0.00755095
Volume: 0.00780526

These values tell us that if the weight increase by 1kg, the CO2 emission increases by 0.00755095g.

And if the engine size (Volume) increases by 1 cm 3 , the CO2 emission increases by 0.00780526 g.

I think that is a fair guess, but let test it!

We have already predicted that if a car with a 1300cm 3 engine weighs 2300kg, the CO2 emission will be approximately 107g.

What if we increase the weight with 1000kg?

Example

Copy the example from before, but change the weight from 2300 to 3300:

import pandas
from sklearn import linear_model

X = df[[‘Weight’, ‘Volume’]]y = df[‘CO2’]

regr = linear_model.LinearRegression()
regr.fit(X, y)

predictedCO2 = regr.predict([[3300, 1300]])

Result:

We have predicted that a car with 1.3 liter engine, and a weight of 3300 kg, will release approximately 115 grams of CO2 for every kilometer it drives.

Which shows that the coefficient of 0.00755095 is correct:

107.2087328 + (1000 * 0.00755095) = 114.75968

Источник

Пример решения задачи множественной регрессии с помощью Python

Добрый день, уважаемые читатели.
В прошлых статьях, на практических примерах, мной были показаны способы решения задач классификации (задача кредитного скоринга) и основ анализа текстовой информации (задача о паспортах). Сегодня же мне бы хотелось коснуться другого класса задач, а именно восстановления регрессии. Задачи данного класса, как правило, используются при прогнозировании.
Для примера решения задачи прогнозирования, я взял набор данных Energy efficiency из крупнейшего репозитория UCI. В качестве инструментов по традиции будем использовать Python c аналитическими пакетами pandas и scikit-learn.

Описание набора данных и постановка задачи

Дан набор данных, котором описаны следующие атрибуты помещения:

Поле	Описание	Тип
X1	Относительная компактность	FLOAT
X2	Площадь	FLOAT
X3	Площадь стены	FLOAT
X4	Площадь потолка	FLOAT
X5	Общая высота	FLOAT
X6	Ориентация	INT
X7	Площадь остекления	FLOAT
X8	Распределенная площадь остекления	INT
y1	Нагрузка при обогреве	FLOAT
y2	Нагрузка при охлаждении	FLOAT

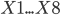
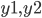
В нем — характеристики помещения на основании которых будет проводиться анализ, а — значения нагрузки, которые надо спрогнозировать.

Предварительный анализ данных

Для начала загрузим наши данные и посмотрим на них:

from pandas import read_csv, DataFrame from sklearn.neighbors import KNeighborsRegressor from sklearn.linear_model import LinearRegression, LogisticRegression from sklearn.svm import SVR from sklearn.ensemble import RandomForestRegressor from sklearn.metrics import r2_score from sklearn.cross_validation import train_test_split dataset = read_csv('EnergyEfficiency/ENB2012_data.csv',';') dataset.head() 

X1	X2	X3	X4	X5	X6	X7	X8	Y1	Y2
0	0.98	514.5	294.0	110.25	7	2	0	0	15.55	21.33
1	0.98	514.5	294.0	110.25	7	3	0	0	15.55	21.33
2	0.98	514.5	294.0	110.25	7	4	0	0	15.55	21.33
3	0.98	514.5	294.0	110.25	7	5	0	0	15.55	21.33
4	0.90	563.5	318.5	122.50	7	2	0	0	20.84	28.28

Теперь давайте посмотрим не связаны ли между собой какие-либо атрибуты. Сделать это можно рассчитав коэффициенты корреляции для всех столбцов. Как это сделать было описано в предыдущей статье:

dataset = dataset.drop(['X1','X4'], axis=1) dataset.head() 

Помимо этого, можно заметить, что поля Y1 и Y2 очень тесно коррелируют между собой. Но, т. к. нам надо спрогнозировать оба значения мы их оставляем «как есть».

Выбор модели

Отделим от нашей выборки прогнозные значения:

trg = dataset[['Y1','Y2']] trn = dataset.drop(['Y1','Y2'], axis=1) 

, где 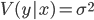— условная дисперсия зависимой величины у по фактору х.
Коэффициент принимает значение на промежутке 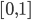и чем он ближе к 1 тем сильнее зависимость.
Ну что же теперь можно перейти непосредственно к построению модели и выбору модели. Давайте поместим все наши модели в один список для удобства дальнейшего анализа:

 models = [LinearRegression(), # метод наименьших квадратов RandomForestRegressor(n_estimators=100, max_features ='sqrt'), # случайный лес KNeighborsRegressor(n_neighbors=6), # метод ближайших соседей SVR(kernel='linear'), # метод опорных векторов с линейным ядром LogisticRegression() # логистическая регрессия ] 

Итак модели готовы, теперь мы разобьем наши исходные данные на 2 подвыборки: тестовую и обучающую. Кто читал мои предыдущие статьи знает, что сделать это можно с помощью функции train_test_split() из пакета scikit-learn:

Xtrn, Xtest, Ytrn, Ytest = train_test_split(trn, trg, test_size=0.4) 

Теперь, т. к. нам надо спрогнозировать 2 параметра , надо построить регрессию для каждого из них. Кроме этого, для дальнейшего анализа, можно записать полученные результаты во временный DataFrame. Сделать это можно так:

 #создаем временные структуры TestModels = DataFrame() tmp = <> #для каждой модели из списка for model in models: #получаем имя модели m = str(model) tmp['Model'] = m[:m.index('(')] #для каждого столбцам результирующего набора for i in xrange(Ytrn.shape[1]): #обучаем модель model.fit(Xtrn, Ytrn[:,i]) #вычисляем коэффициент детерминации tmp['R2_Y%s'%str(i+1)] = r2_score(Ytest[:,0], model.predict(Xtest)) #записываем данные и итоговый DataFrame TestModels = TestModels.append([tmp]) #делаем индекс по названию модели TestModels.set_index('Model', inplace=True) 

Как можно заметить из кода выше, для расчета коэффициента используется функция r2_score().
Итак, данные для анализа получены. Давайте теперь построим графики и посмотрим какая модель показала лучший результат:

fig, axes = plt.subplots(ncols=2, figsize=(10,4)) TestModels.R2_Y1.plot(ax=axes[0], kind='bar', title='R2_Y1') TestModels.R2_Y2.plot(ax=axes[1], kind='bar', color='green', title='R2_Y2') 

Анализ результатов и выводы

Из графиков, приведенных выше, можно сделать вывод, что лучше других с задачей справился метод RandomForest (случайный лес). Его коэффициенты детерминации выше остальных по обоим переменным:
ля дальнейшего анализа давайте заново обучим нашу модель:

model = models[1] model.fit(Xtrn, Ytrn) 

При внимательном рассмотрении, может возникнуть вопрос, почему в предыдущий раз и делили зависимую выборку Ytrn на переменные(по столбцам), а теперь мы этого не делаем.
Дело в том, что некоторые методы, такие как RandomForestRegressor, может работать с несколькими прогнозируемыми переменными, а другие (например SVR) могут работать только с одной переменной. Поэтому на при предыдущем обучении мы использовали разбиение по столбцам, чтобы избежать ошибки в процессе построения некоторых моделей.
Выбрать модель это, конечно же, хорошо, но еще неплохо бы обладать информацией, как каждый фактор влиет на прогнозное значение. Для этого у модели есть свойство feature_importances_.
С помощью него, можно посмотреть вес каждого фактора в итоговой моделей:

model.feature_importances_ 

array([ 0.40717901, 0.11394948, 0.34984766, 0.00751686, 0.09158358,
0.02992342])

В нашем случае видно, что больше всего на нагрузку при обогреве и охлаждении влияют общая высота и площадь. Их общий вклад в прогнозной модели около 72%.
Также необходимо отметить, что по вышеуказанной схеме можно посмотреть влияние каждого фактора отдельно на обогрев и отдельно на охлаждение, но т. к. эти факторы у нас очень тесно коррелируют между собой (), мы сделали общий вывод по ним обоим который и был написан выше.

Заключение

В статье я постарался показать основные этапы при регрессионном анализе данных с помощью Python и аналитческих пакетов pandas и scikit-learn.
Необходимо отметить, что набор данных специально выбирался таким образом чтобы быть максимально формализованым и первичная обработка входных данных была бы минимальна. На мой взгляд статья будет полезна тем, кто только начинает свой путь в анализе данных, а также тем кто имеет хорошую теоретическую базу, но выбирает инструментарий для работы.

Источник