Matrix multiply in java

Matrix Multiplication in Java

In this post, we will discuss Matrix Multiplication in Java | How to find Multiplication of two matrix in java? How to write a Java program to multiply two matrices? What are the different techniques to find the matrix multiplication in Java? Since a matrix is also known as an array of arrays, therefore matrix multiplication can be called array multiplication in Java.

What is Matrix Multiplication?

Let A be an m×k matrix and B be a k ×n matrix. The product of A and B, denoted by AB, is the m × n matrix with its (i, j )th entry equal to the sum of the products of the corresponding elements from the ith row of A and the jth column of B. In other words, if AB =[c_ij], then c_ij = a_i1b_1j + a_i2b_2j +···+a_ikb_kj.

Condition for the Matrix multiplication:- The product of two matrices is not defined when the number of columns in the first matrix and the number of rows in the second matrix are not the same.

Example of Matrix Multiplication,

The product of A and B is denoted as AB and it can be calculated as AB=
(a11*b11+a12*b21) (a11*b12+a12*b22)
(a21*b11+a22*b21) (a21*b12+a22*b22)

Example using 2×2 matrices,

C = 1*6+3*4 1*8+3*2 7*6+5*4 7*8+5*2 = 18 14 62 66

Java Method to find Matrix Multiplication for Square Matrix

// method to calculate product of two matrix public static int[][] multiplyMatrix(int[][] a, int[][] b) < // find size of matrix // (Assuming both matrix is square matrix // of same size) int size = a.length; // declare new matrix to store result int product[][] = new int[size][size]; // find product of both matrices // outer loop for (int i = 0; i < size; i++) < // inner-1 loop for (int j = 0; j < size; j++) < // assign 0 to the current element product[i][j] = 0; // inner-2 loop for (int k = 0; k < size; k++) < product[i][j] += a[i][k] * b[k][j]; >> > return product; >

Time Complexity:- O(N 3 )

Why does it need three for loops? For accessing all the elements of any matrix we need two for loop. But for finding the product requires one additional for loop. Therefore the time complexity is O(N 3 ).

Matrix Multiplication in Java Using Methods

In this program, values for the matrices are already given just call the method to multiply both matrices, and then display the resultant matrix.

import java.util.Arrays; public class Matrix < // main method public static void main(String[] args) < // declare and initialize a matrix int a[][] = < < 1, 3 >, < 7, 5 >>; int b[][] = < < 6, 8 >, < 4, 2 >>; // find size of matrix // (Assuming both matrix is square matrix // of same size) int size = a.length; // 2 // declare new matrix to store result (2x2) int c[][] = new int[size][size]; // multiplication of matrix c = multiplyMatrix(a, b); // display all matrices System.out.println("A = " + Arrays.deepToString(a)); System.out.println("B = " + Arrays.deepToString(b)); System.out.println("C (Product) = " + Arrays.deepToString(c)); > // method to calculate product of two matrix public static int[][] multiplyMatrix(int[][] a, int[][] b) < // find size of matrix // (Assuming both matrix is square matrix // of same size) int size = a.length; // declare new matrix to store result int product[][] = new int[size][size]; // find product of both matrices // outer loop for (int i = 0; i < size; i++) < // inner-1 loop for (int j = 0; j < size; j++) < // assign 0 to the current element product[i][j] = 0; // inner-2 loop for (int k = 0; k < size; k++) < product[i][j] += a[i][k] * b[k][j]; >> > return product; > >

A = [[ 1, 3 ] , [ 7, 5 ]]
B = [[ 6, 8 ] , [ 4, 2 ]]
C (Product) = [[ 18, 14 ] , [ 62, 66 ]]

In this program, to display the matrix we had used deepToString() method of the Arrays class, but you can also use the nested loops. See:- Different ways to print array in Java

Matrix Multiplication by taking Input from the User

In the above program both matrices A and B were initialized within the program, now let us see another Java program for matrix multiplication by taking input values from users using Scanner. If you want then you can also use BufferedReader class.

import java.util.Scanner; public class Matrix < // create Scanner class object to read input private static Scanner scan = new Scanner(System.in); // main method public static void main(String[] args) < // declare variables int size = 0; int a[][] = null; // first matrix int b[][] = null; // second matrix int c[][] = null; // resultant matrix // ask size // (assume matrices are square matrix with same size) System.out.println("Enter the Size of Matrix,"); System.out.println("Enter 2 for 2x2, 3 for 3x3 and e.t.c: "); size = scan.nextInt(); // initialize matrices a = new int[size][size]; b = new int[size][size]; c = new int[size][size]; // read matrix A and B System.out.println("Enter Matrix A: "); a = readMatrix(a); System.out.println("Enter Matrix B: "); b = readMatrix(b); // multiplication of matrix c = multiplyMatrix(a, b); // display resultant matrix System.out.println("Result Matrix: "); for(int i=0; iSystem.out.println(); // new line > > // method to read matrix elements as input public static int[][] readMatrix(int[][] temp) < for (int i = 0; i < temp.length; i++) < for (int j = 0; j < temp[0].length; j++) < // read matrix elements temp[i][j] = scan.nextInt(); >> return temp; > // method to calculate product of two matrix public static int[][] multiplyMatrix(int[][] a, int[][] b) < // find size of matrix // (Assuming both matrix is square matrix // of same size) int size = a.length; // declare new matrix to store result int product[][] = new int[size][size]; // find product of both matrices // outer loop for (int i = 0; i < size; i++) < // inner-1 loop for (int j = 0; j < size; j++) < // assign 0 to the current element product[i][j] = 0; // inner-2 loop for (int k = 0; k < size; k++) < product[i][j] += a[i][k] * b[k][j]; >> > return product; > >

Enter the Size of Matrix,
Enter 2 for 2×2, 3 for 3×3 and e.t.c:
3
Enter Matrix A:
1 2 3
4 5 6
7 8 9
Enter Matrix B:
5 6 7
8 9 10
3 1 2
Result Matrix:
30 27 33
78 75 90
126 123 147

In this program, we had created Scanner class object as a private static variable which is outside of the main method because we need to read input values in two methods, in the main method to read row and column values and in the readMatrix() method to read matrix elements. Therefore instead of creating Scanner class objects in both classes separately, it is better to create them as a static variable only once and use it multiple times anywhere in the program.

Program for Both Square and Non Square matrix

In the above examples we were assuming that matrix is a square matrix, therefore those methods will work only for a square matrix. For non-square matrix, row and column sizes vary. Below Java program is capable to calculate the product of both Square and Non-Square matrices.

public class Matrix < // main method public static void main(String[] args) < // declare and initialize a 3x2 matrix int a[][] = < < 1, 2 >, < 3, 4 >, >; // declare and initialize a 2x4 matrix int b[][] = < < 6, 7, 8, 9 >, < 1, 2, 3, 4 >>; // find row size of first matrix int row = a.length; // 3 // find column size of second matrix int column = b[0].length; // 4 // declare new matrix to store result (3x4) int c[][] = new int[row][column]; // multiplication of matrix c = multiplyMatrix(a, b); // display all matrices System.out.println("Matrix A = "); displayMatrix(a); System.out.println("Matrix B = "); displayMatrix(b); System.out.println("Matrix C (Product) = "); displayMatrix(c); > // method to display the matrix public static void displayMatrix(int[][] matrix) < // outer loop for row for(int i=0; iSystem.out.println(); // new line > > // method to calculate product of two matrix // matrices can be square or non-square matrix public static int[][] multiplyMatrix(int[][] a, int[][] b) < // find row size of first matrix int row = a.length; // find column size of second matrix int column = b[0].length; // declare new matrix to store result int product[][] = new int[row][column]; // find product of both matrices // outer loop upto row of A for (int i = 0; i < row; i++) < // inner-1 loop utp0 column of B for (int j = 0; j < column; j++) < // assign 0 to the current element product[i][j] = 0; // inner-2 loop utpo A[0].length for (int k = 0; k < a[0].length; k++) < product[i][j] += a[i][k] * b[k][j]; >> > return product; > >

Matrix A =
1 2
3 4
5 6
Matrix B =
6 7 8 9
1 2 3 4
Matrix C (Product) =
8 11 14 17
22 29 36 43
36 47 58 69

Using Divide and Conquer Method

In the divide and conquer method we say that if the problem is larger then we break the problem into sub-problems and solve those sub-problems. Later combine the solutions of sub-problems to get the solution for the actual problem.

If it is a smaller problem then it can be solved directly but if it is a large problem then using divide and conquer break them into small problems. Therefore let us see the solution for the smaller problems.

To solve our problem assume 2×2 is the smallest square matrix. Let A and B be two different matrices.

Since this method requires 8 multiplication and 4 addition therefore it requires constant time. The time complexity is:- O(N 3 )

What if the size is greater than 2×2? We assume that the matrices are having dimensions in powers of 2 like 2×2, 4×4, 8×8, 16×16, 256×256, and e.t.c. If it is not of power 2×2 then we can fill zeros and makes it a square matrix of 2×2.

The next matrix multiplication algorithm given by Strassen is also using the divide and conquer technique and gives better performance O(N2.8041) therefore we are not writing the program for this method.

Strassen’s Matrix Multiplication in Java

Strassen’s had given another algorithm for finding the matrix multiplication. Unlike a simple divide and conquer method which uses 8 multiplications and 4 additions, Strassen’s algorithm uses 7 multiplications which reduces the time complexity of the matrix multiplication algorithm a little bit.

The addition and subtraction operation takes less time compared to the multiplication process. In Strassen’s matrix multiplication algorithm, the number of multiplication was reduced but the number of addition and subtraction increased.

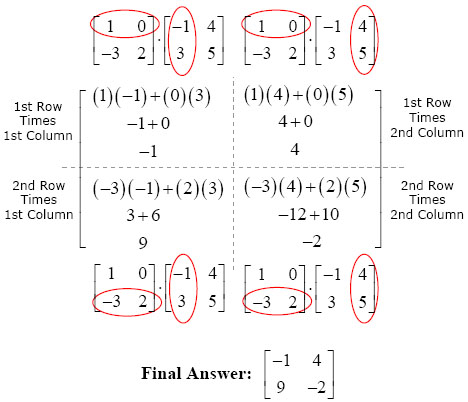
/** ** Java Program to Implement Strassen Algorithm **/ package com.know.program; import java.util.Scanner; public class Matrix < // create Scanner class object to read input private static Scanner scan = new Scanner(System.in); // method to calculate product of two matrix // Strassen Algorithm public int[][] multiply(int[][] a, int[][] b) < // find size of matrix int n = a.length; // create new matrix to store resultant int[][] c = new int[n][n]; /** base case **/ if (n == 1) c[0][0] = a[0][0] * b[0][0]; else < /* general case */ int[][] A11 = new int[n / 2][n / 2]; int[][] A12 = new int[n / 2][n / 2]; int[][] A21 = new int[n / 2][n / 2]; int[][] A22 = new int[n / 2][n / 2]; int[][] B11 = new int[n / 2][n / 2]; int[][] B12 = new int[n / 2][n / 2]; int[][] B21 = new int[n / 2][n / 2]; int[][] B22 = new int[n / 2][n / 2]; // divide matrix A into 4 halves split(a, A11, 0, 0); split(a, A12, 0, n / 2); split(a, A21, n / 2, 0); split(a, A22, n / 2, n / 2); // divide matrix B into 4 halves split(b, B11, 0, 0); split(b, B12, 0, n / 2); split(b, B21, n / 2, 0); split(b, B22, n / 2, n / 2); /** * p1 = (A11 + A22)(B11 + B22) * p2 = (A21 + A22) B11 * p3 = A11 (B12 - B22) * p4 = A22 (B21 - B11) * p5 = (A11 + A12) B22 * p6 = (A21 - A11) (B11 + B12) * p7 = (A12 - A22) (B21 + B22) **/ int[][] p1 = multiply(add(A11, A22), add(B11, B22)); int[][] p2 = multiply(add(A21, A22), B11); int[][] p3 = multiply(A11, sub(B12, B22)); int[][] p4 = multiply(A22, sub(B21, B11)); int[][] p5 = multiply(add(A11, A12), B22); int[][] p6 = multiply(sub(A21, A11), add(B11, B12)); int[][] p7 = multiply(sub(A12, A22), add(B21, B22)); /** * C11 = p1 + p4 - p5 + p7 * C12 = p3 + p5 * C21 = p2 + p4 * C22 = p1 - p2 + p3 + p6 **/ int[][] C11 = add(sub(add(p1, p4), p5), p7); int[][] C12 = add(p3, p5); int[][] C21 = add(p2, p4); int[][] C22 = add(sub(add(p1, p3), p2), p6); /** join 4 halves into one result matrix **/ join(C11, c, 0, 0); join(C12, c, 0, n / 2); join(C21, c, n / 2, 0); join(C22, c, n / 2, n / 2); >// end-of-else-part // return resultant matrix return c; > // method to add two matrices public int[][] add(int[][] a, int[][] b) < int n = a.length; int[][] c = new int[n][n]; for (int i = 0; i < n; i++) for (int j = 0; j < n; j++) c[i][j] = a[i][j] + b[i][j]; return c; >// method to subract two matrices public int[][] sub(int[][] a, int[][] b) < int n = a.length; int[][] c = new int[n][n]; for (int i = 0; i < n; i++) for (int j = 0; j < n; j++) c[i][j] = a[i][j] - b[i][j]; return c; >// method to split parent matrix into child matrices public void split(int[][] parentMatrix, int[][] childMatrix, int fromIndex, int toIndex) < for (int i1=0, i2=fromIndex; i1 < childMatrix.length; i1++, i2++) for (int j1=0, j2=toIndex; j1 < childMatrix.length; j1++, j2++) childMatrix[i1][j1] = parentMatrix[i2][j2]; >// method to join child matrices into parent matrix public void join(int[][] childMatrix, int[][] parentMatrix, int fromIndex, int toIndex) < for (int i1=0, i2=fromIndex; i1 < childMatrix.length; i1++, i2++) for (int j1=0, j2=toIndex; j1 < childMatrix.length; j1++, j2++) parentMatrix[i2][j2] = childMatrix[i1][j1]; >// method to read matrix elements as input public int[][] readMatrix(int[][] temp) < for (int i = 0; i < temp.length; i++) < for (int j = 0; j < temp[0].length; j++) < // read matrix elements temp[i][j] = scan.nextInt(); >> return temp; > // main method public static void main(String[] args) < System.out.println("Strassen Multiplication Algorithm Test\n"); // Create an object of Matrix class Matrix mtx = new Matrix(); // declare variables int size = 0; int a[][] = null; // first matrix int b[][] = null; // second matrix int c[][] = null; // resultant matrix System.out.print("Enter Matrix Order: "); size = scan.nextInt(); // initialize matrices a = new int[size][size]; b = new int[size][size]; c = new int[size][size]; // read matrix A and B System.out.println("Enter Matrix A: "); a = mtx.readMatrix(a); System.out.println("Enter Matrix B: "); b = mtx.readMatrix(b); // multiplication of matrix c = mtx.multiply(a, b); // display resultant matrix System.out.println("Resultant Matrix: "); for(int i=0; iSystem.out.println(); // new line > > >

Output for different test-cases:-

Strassen Multiplication Algorithm Test

Enter Matrix Order: 2
Enter Matrix A:
1 3
7 5
Enter Matrix B:
6 8
4 2
Resultant Matrix:
18 14
62 66

Strassen Multiplication Algorithm Test

Enter Matrix Order: 4
Enter Matrix A:
5 2 6 1
0 6 2 0
3 8 1 4
1 8 5 6
Enter Matrix B:
7 5 8 0
1 8 2 6
9 4 3 8
5 3 7 9
Resultant Matrix:
96 68 69 69
24 56 18 52
58 95 71 92
90 107 81 142

Time complexity = O(n log 7/2) = O(n 2.8074 )

The O(n 2.8074 ) is slightly lesser than O(n 3 ) but this method is usually not preferred for practical purposes.

The constants used in Strassen’s method are high and most of the time the first basic method works better. To find multiplication of Sparse matrices (which contains very few non-zero elements) better algorithms are available. The submatrices in recursion take extra space. Because of the limited precision of computer arithmetic on noninteger values, larger errors accumulate in Strassen’s algorithm than in the first basic method.

If you enjoyed this post, share it with your friends. Do you want to share more information about the topic discussed above or do you find anything incorrect? Let us know in the comments. Thank you!

Источник

Matrix Multiplication In Java – 4 Ways | Programs

Matrix Multiplication In Java – Here, we will discuss the various methods on how to multiply two matrices using Java. The compiler has been added so that you can execute the given programs yourself, alongside suitable examples and sample outputs.

How To Perform Matrix Multiplication:

Matrix multiplication is a simple binary operation that produces a single matrix from the entries of two given matrices. When two Matrices P & Q of order a*b and b*c are multiplied, the resultant matrix will be of the order a*c.

Here, the a entries across a row of P are multiplied with the b entries down a column of Q to produce the entry of PQ. The example given below explains the multiplication between two 2*2 matrices.

Matrix Multiplication In Java – Using For Loop

1) Condition for multiplication of two matrices is -1st matrix column number equal to 2nd matrix row number.

2) Read row,column numbers of matrix1, matrix2 and check column number of matrix1= row number of matrix2. If condition is true then

a) Insert the elements at matrix1 using two for loops:

b) Similarly insert the elements at matrix2 using 2 loops with the structures for (i=0;i

Источник

Matrix Programs in Java

While we believe that this content benefits our community, we have not yet thoroughly reviewed it. If you have any suggestions for improvements, please let us know by clicking the “report an issue“ button at the bottom of the tutorial.

A Matrix is a rectangular array. The elements are arranged in the rows and columns. In this tutorial, we will look at some matrix programs in Java.

Graphical Representation of Matrix

Matrix in Java

We can implement a matrix using two dimensional array in Java. The element at row “r” and column “c” can be accessed using index “array[r][c]”.

Matrix Programs in Java

Since we are using two-dimensional arrays to create a matrix, we can easily perform various operations on its elements. In this tutorial, we will learn how to create a matrix from user input. Then we will add, subtract, and multiply two matrices and print the result matrix on the console.

1. Adding Two Matrix

Here is the simple program to populate two matrices from the user input. Then add its elements at the corresponding indices to get the addition of the matrices. Finally, we will print the sum of the matrices.

package com.journaldev.examples; import java.util.Scanner; public class MatrixPrograms < public static void main(String[] args) < System.out.println("Please enter the rows in the matrix"); Scanner sc = new Scanner(System.in); int row = sc.nextInt(); System.out.println("Please enter the columns in the matrix"); int column = sc.nextInt(); int[][] first = new int[row][column]; int[][] second = new int[row][column]; for (int r = 0; r < row; r++) < for (int c = 0; c < column; c++) < System.out.println(String.format("Enter first[%d][%d] integer", r, c)); first[r][c] = sc.nextInt(); >> for (int r = 0; r < row; r++) < for (int c = 0; c < column; c++) < System.out.println(String.format("Enter second[%d][%d] integer", r, c)); second[r][c] = sc.nextInt(); >> // close the scanner sc.close(); // print both matrices System.out.println("First Matrix:\n"); print2dArray(first); System.out.println("Second Matrix:\n"); print2dArray(second); // sum of matrices sum(first, second); > // below code doesn't take care of exceptions private static void sum(int[][] first, int[][] second) < int row = first.length; int column = first[0].length; int[][] sum = new int[row][column]; for (int r = 0; r < row; r++) < for (int c = 0; c < column; c++) < sum[r][c] = first[r][c] + second[r][c]; >> System.out.println("\nSum of Matrices:\n"); print2dArray(sum); > private static void print2dArray(int[][] matrix) < for (int r = 0; r < matrix.length; r++) < for (int c = 0; c < matrix[0].length; c++) < System.out.print(matrix[r][c] + "\t"); >System.out.println(); > > > 

2. Subtracting Two Matrices

Here is the function to subtraction second matrix elements from the first matrix and then print the result matrix.

private static void subtract(int[][] first, int[][] second) < int row = first.length; int column = first[0].length; int[][] sum = new int[row][column]; for (int r = 0; r < row; r++) < for (int c = 0; c < column; c++) < sum[r][c] = first[r][c] - second[r][c]; >> System.out.println("\nSubtraction of Matrices:\n"); print2dArray(sum); > 

3. Multiplying Two Matrices

private static void multiply(int[][] first, int[][] second) < int row = first.length; int column = first[0].length; int[][] sum = new int[row][column]; for (int r = 0; r < row; r++) < for (int c = 0; c < column; c++) < sum[r][c] = first[r][c] * second[r][c]; >> System.out.println("\nMultiplication of Matrices:\n"); print2dArray(sum); > 

Thanks for learning with the DigitalOcean Community. Check out our offerings for compute, storage, networking, and managed databases. Learn more about us

Источник