Matrices program in java

Matrix Programs in Java

While we believe that this content benefits our community, we have not yet thoroughly reviewed it. If you have any suggestions for improvements, please let us know by clicking the “report an issue“ button at the bottom of the tutorial.

A Matrix is a rectangular array. The elements are arranged in the rows and columns. In this tutorial, we will look at some matrix programs in Java.

Graphical Representation of Matrix

Matrix in Java

We can implement a matrix using two dimensional array in Java. The element at row “r” and column “c” can be accessed using index “array[r][c]”.

Matrix Programs in Java

Since we are using two-dimensional arrays to create a matrix, we can easily perform various operations on its elements. In this tutorial, we will learn how to create a matrix from user input. Then we will add, subtract, and multiply two matrices and print the result matrix on the console.

1. Adding Two Matrix

Here is the simple program to populate two matrices from the user input. Then add its elements at the corresponding indices to get the addition of the matrices. Finally, we will print the sum of the matrices.

package com.journaldev.examples; import java.util.Scanner; public class MatrixPrograms < public static void main(String[] args) < System.out.println("Please enter the rows in the matrix"); Scanner sc = new Scanner(System.in); int row = sc.nextInt(); System.out.println("Please enter the columns in the matrix"); int column = sc.nextInt(); int[][] first = new int[row][column]; int[][] second = new int[row][column]; for (int r = 0; r < row; r++) < for (int c = 0; c < column; c++) < System.out.println(String.format("Enter first[%d][%d] integer", r, c)); first[r][c] = sc.nextInt(); >> for (int r = 0; r < row; r++) < for (int c = 0; c < column; c++) < System.out.println(String.format("Enter second[%d][%d] integer", r, c)); second[r][c] = sc.nextInt(); >> // close the scanner sc.close(); // print both matrices System.out.println("First Matrix:\n"); print2dArray(first); System.out.println("Second Matrix:\n"); print2dArray(second); // sum of matrices sum(first, second); > // below code doesn't take care of exceptions private static void sum(int[][] first, int[][] second) < int row = first.length; int column = first[0].length; int[][] sum = new int[row][column]; for (int r = 0; r < row; r++) < for (int c = 0; c < column; c++) < sum[r][c] = first[r][c] + second[r][c]; >> System.out.println("\nSum of Matrices:\n"); print2dArray(sum); > private static void print2dArray(int[][] matrix) < for (int r = 0; r < matrix.length; r++) < for (int c = 0; c < matrix[0].length; c++) < System.out.print(matrix[r][c] + "\t"); >System.out.println(); > > > 

2. Subtracting Two Matrices

Here is the function to subtraction second matrix elements from the first matrix and then print the result matrix.

private static void subtract(int[][] first, int[][] second) < int row = first.length; int column = first[0].length; int[][] sum = new int[row][column]; for (int r = 0; r < row; r++) < for (int c = 0; c < column; c++) < sum[r][c] = first[r][c] - second[r][c]; >> System.out.println("\nSubtraction of Matrices:\n"); print2dArray(sum); > 

3. Multiplying Two Matrices

private static void multiply(int[][] first, int[][] second) < int row = first.length; int column = first[0].length; int[][] sum = new int[row][column]; for (int r = 0; r < row; r++) < for (int c = 0; c < column; c++) < sum[r][c] = first[r][c] * second[r][c]; >> System.out.println("\nMultiplication of Matrices:\n"); print2dArray(sum); > 

Thanks for learning with the DigitalOcean Community. Check out our offerings for compute, storage, networking, and managed databases. Learn more about us

Источник

Java Matrix Example

In this article, we will discuss the Matrix in Java. We will cover what matrix are, how to create a Java matrix, how to traverse a matrix, and some of the common operations on matrices.

1. What is a Matrix in Java?

A Matrix is a rectangular array. The elements are arranged in rows and columns. Since there are two directions or dimensions of traversing a matrix, they are also known as 2D arrays.

2. Representation of Matrix

In this section, we will discuss the representation of a matrix. In simple terms, a matrix can be visualized as a table where each row in the table represents one row of the matrix, and the number of columns of the table is determined via the number of columns of the matrix.

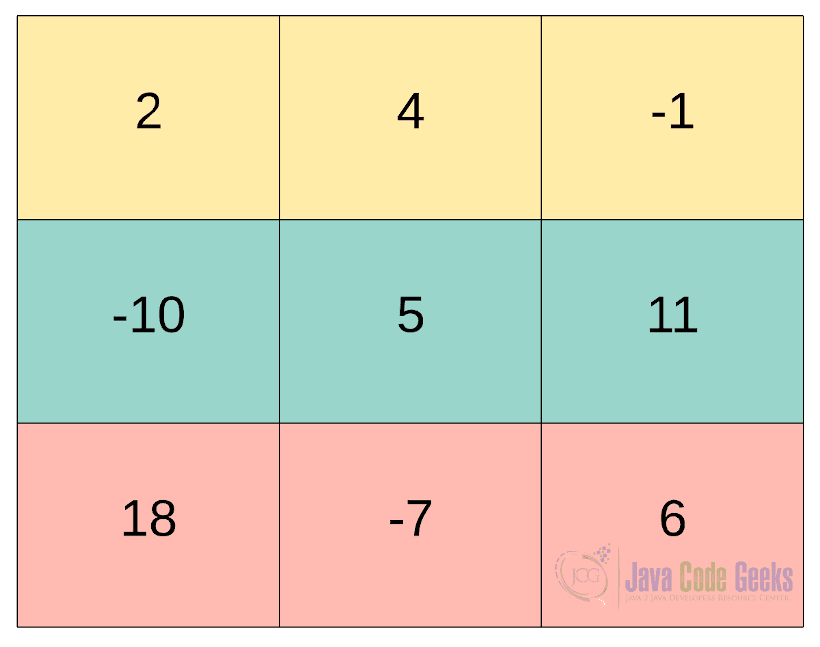
for example, in the snapshot below, we show an example of a matrix, which is referenced from here.

As per the image showed above, each element of the above matrix can be represented in Java as shown below,

As shown in the above snapshot, the first value, 2, from the matrix will be stored at the first index for both row and column [0,0]. After that, we first move on to fill the first row and then repeat the process for all the remaining rows.

3. Common Operation on Matrices

In this section, we will discuss some of the common operations on the matrices, including addition and multiplication of 2 matrices, transpose a matrix, etc.

We will first discuss how to add 2 matrices. In order to add 2 matrices, there is a pre-condition, the number of rows in both matrices should be equal and the number of columns in both should be equal.

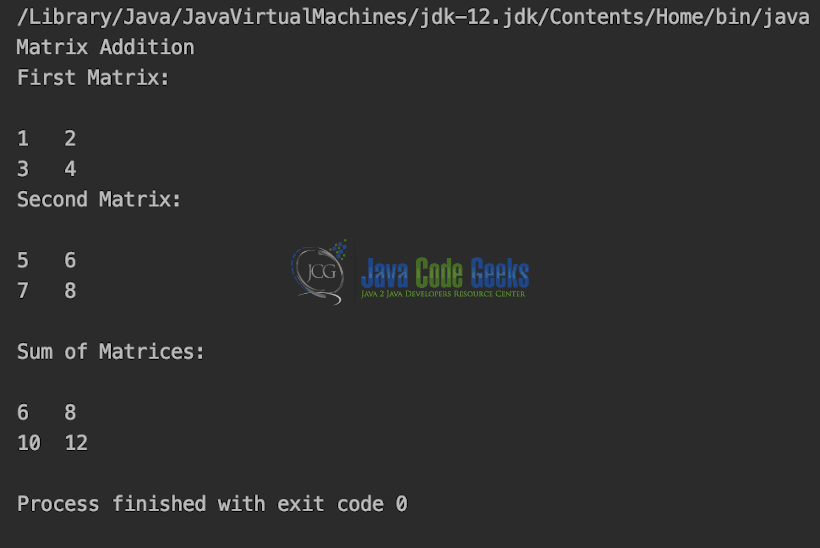
In the code snippet, we will show the Matrix addition in action. MatrixAddition.java

package org.example; public class MatrixAddition < public static void main(String[] args) < System.out.println("Matrix Addition"); int[][] firstMatrix = , >; int[][] secondMatrix = , >; System.out.println("First Matrix:\n"); displayMatrix(firstMatrix); System.out.println("Second Matrix:\n"); displayMatrix(secondMatrix); sum(firstMatrix, secondMatrix); > private static void sum(int[][] first, int[][] second) < int row = first.length; int column = first[0].length; int[][] sum = new int[row][column]; for (int r = 0; r < row; r++) < for (int c = 0; c < column; c++) < sum[r][c] = first[r][c] + second[r][c]; >> System.out.println("\nSum of Matrices:\n"); displayMatrix(sum); > private static void displayMatrix(int[][] matrix) < for (int r = 0; r < matrix.length; r++) < for (int c = 0; c < matrix[0].length; c++) < System.out.print(matrix[r][c] + "\t"); >System.out.println(); > > >

The output is shown in the snapshot below.

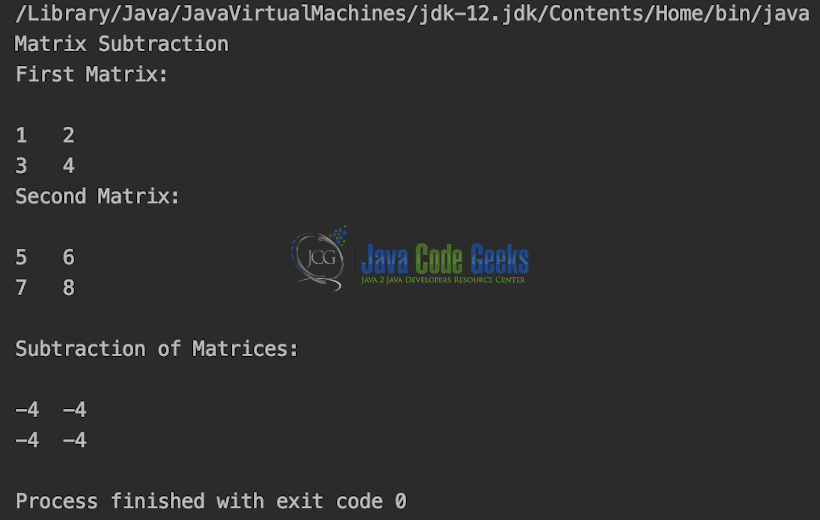
Another similar operation with the same prerequisites as matrix addition is matrix subtraction. MatrixSubtraction.java

package org.example; public class MatrixSubtraction < public static void main(String[] args) < System.out.println("Matrix Subtraction"); int[][] firstMatrix = , >; int[][] secondMatrix = , >; System.out.println("First Matrix:\n"); displayMatrix(firstMatrix); System.out.println("Second Matrix:\n"); displayMatrix(secondMatrix); subtract(firstMatrix, secondMatrix); > private static void subtract(int[][] first, int[][] second) < int row = first.length; int column = first[0].length; int[][] diff = new int[row][column]; for (int r = 0; r < row; r++) < for (int c = 0; c < column; c++) < diff[r][c] = first[r][c] - second[r][c]; >> System.out.println("\nSubtraction of Matrices:\n"); displayMatrix(diff); > private static void displayMatrix(int[][] matrix) < for (int r = 0; r < matrix.length; r++) < for (int c = 0; c < matrix[0].length; c++) < System.out.print(matrix[r][c] + "\t"); >System.out.println(); > > >

The output is shown in the snapshot below,

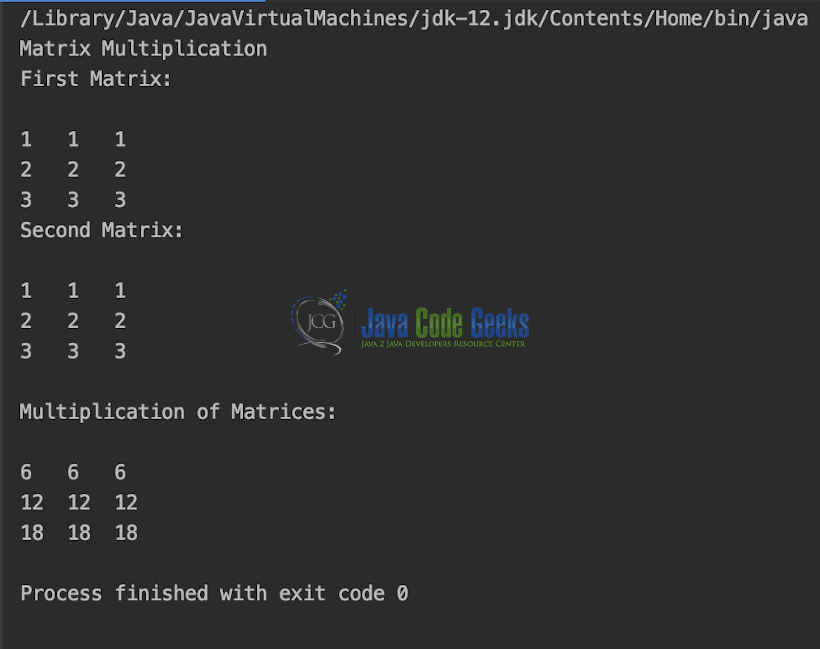
The next operation which we will discuss is the Matrix multiplication. The pre-requisites are, For matrix multiplication, the number of columns in the first matrix must be equal to the number of rows in the second matrix. MatrixMultiplication.java

package org.example; public class MatrixMultiplication < public static void main(String[] args) < System.out.println("Matrix Multiplication"); int[][] firstMatrix = , , >; int[][] secondMatrix = , , >; System.out.println("First Matrix:\n"); displayMatrix(firstMatrix); System.out.println("Second Matrix:\n"); displayMatrix(secondMatrix); multiply(firstMatrix, secondMatrix); > private static void multiply(int[][] first, int[][] second) < int row = first.length; int column = first[0].length; int[][] product = new int[row][column]; for (int i = 0; i < 3; i++) < for (int j = 0; j < 3; j++) < product[i][j] = 0; for (int k = 0; k < 3; k++) < product[i][j] += first[i][k] * second[k][j]; >> > System.out.println("\nMultiplication of Matrices:\n"); displayMatrix(product); > private static void displayMatrix(int[][] matrix) < for (int r = 0; r < matrix.length; r++) < for (int c = 0; c < matrix[0].length; c++) < System.out.print(matrix[r][c] + "\t"); >System.out.println(); > > >

The output is shown in the snapshot below,

Another common operation of Matrix is Transposition. Transpose of a matrix is obtained by changing rows to columns and columns to rows. MatrixTranspose.java

package org.example; public class MatrixTranspose < static final int N = 4; static void transpose(int A[][], int B[][]) < int i, j; for (i = 0; i < N; i++) for (j = 0; j < N; j++) B[i][j] = A[j][i]; >public static void main(String[] args) < int A[][] = , , , >; int B[][] = new int[N][N], i, j; System.out.println("Transpose of Matrix"); System.out.println("Before Transpose"); display(A); transpose(A, B); System.out.println("After Transpose"); display(B); > private static void display(int[][] b) < int i; int j; for (i = 0; i < N; i++) < for (j = 0; j < N; j++) System.out.print(b[i][j] + " "); System.out.print("\n"); >> >

The output is shown in the snapshot below,

This covers most of the commonly used operations of a matrix.

4. 3rd Party Library

In this section, we will discuss the commons-math3 library. It’s a library from the Apache foundation. Apache Commons Math consists of mathematical functions (erf for instance), structures representing mathematical concepts (like complex numbers, polynomials, vectors, etc.), and algorithms.

In this article, we will cover the linear equation solver. If we have a linear system of equations under the form AX = B where A is a matrix of real numbers, and B a vector of real numbers. Commons Math provides structures to represent both the matrix and the vector, and also provide solvers to find the value of X. AlgebraSolver.java

package org.example; import org.apache.commons.math3.linear.*; public class AlgebraSolver < public static void main(String[] args) < System.out.println("Equation in the form of AX=B solver"); System.out.println("Matrix representing A"); RealMatrix a = new Array2DRowRealMatrix( new double[][], , >, false); System.out.println(a.toString()); System.out.println("Vector Representing B"); RealVector b = new ArrayRealVector(new double[], false); System.out.println(b.toString()); System.out.println("Creating Solver Object"); DecompositionSolver solver = new LUDecomposition(a).getSolver(); System.out.println("Calculation Solution"); RealVector solution = solver.solve(b); System.out.println("Solution is " + solution.toString()); > >

The output is shown in the snapshot below,

Commons-math3 library provides many operations, which are useful in solving the Statistical problems, geometrical problems, and also problems which are related to Machine Learning and optimization, but the discussion of this is beyond the scope of this article. For further details about this library please refer here.

5. Summary

To Summarise, we have covered the basics of matrices including the representation, storage, traversal, and some of the common operations on them. We have also covered a brief introduction of the commons-math3 library, which has some operations specifically for matrices.

Источник