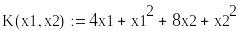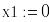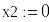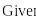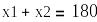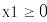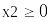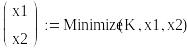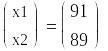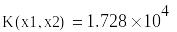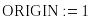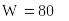Практическая часть
1. Решение задачи целочисленного линейного программирования в Mathcad. В Mathcad нет реализаций методов решения задач целочисленного линейного программирования. Существуют задачи, в которых можно определить пределы изменения значений переменных из системы ограничений, при этом полученные диапазоны изменения значений переменных позволяют получить решение задачи, осуществив полный перебор всех возможных значений переменных. Учитывая небольшое количество возможных вариантов, а также использование программных средств для автоматизации вычислений будем решать такие задачи методом полного или сплошного перебора.
Метод заключается в переборе всех возможных вариантов сочетаний допустимых значений, проверке выполнения для каждого из ограничений и вычислении в удовлетворительных случаях соответствующих значений целевой функции. Из полученного множества значений выбирается максимальное (или минимальное), а набор значений переменных для него и будет решением задачи. Данный метод имеет простой алгоритм и может быть легко реализован с использованием средств программирования пакета Mathcad.
Если вычисление функции требует выполнения нескольких операторов, то в этом случае необходимо использовать операторы из палитры программирования (рис. 4). Составление программы начинается с нажатия кнопки Add line (Добавить строку), после чего в появившиеся шаблоны можно вставлять операторы программирования. Реализуем поэтапно, например, программу вычисления функции, которая задает единичный скачок в точке а (рис. 5).
Рис. 4. Панель программирования
Рис. 5. Создание программы вычисления функции
В этом примере вначале набрано имя функции с двумя формальными параметрами х и а, затем оператор присвоения и нажата кнопка Add line. На втором этапе в первый шаблон вставлен оператор if (если). На следующем этапе в шаблоны оператора if вставлено значение функции при х>а. Затем нажата кнопка otherwise (иначе), и в шаблон этого оператора вставлено нулевое значение функции, которое она принимает при х Обращение к функции с фактическими параметрами дает требуемые значения функции.
В более сложных программах необходима операция присвоения. Оператор присвоения в палитре программирования изображен в виде стрелки, направленной влево: .
Рассмотрим пример использования оператора цикла for (для), показанный на рис. 6. После ввода оператора присвоения нажать кнопка Add line дважды.
Рис. 6. Программа с оператором цикла for
На первом этапе обнуляем переменную суммирования s и вводим во вторую строку программы оператор for, получая в результате и третью строку — шаблон для тела цикла. Далее вставляем в шаблоны для оператора цикла имя циклической переменной и пределы ее изменения. На следующем этапе вводим оператор тела цикла, осуществляющий суммирование квадратов целых чисел и, добавляя еще одну строку нажатием Add line, в последнюю строку программы вводим имя переменной s как результат выполнения программы — суммы квадратов всех целых чисел от m до n.
Пример решения задачи целочисленного линейного программирования в Mathcad. Предприниматель для приобретения оборудования выделяет 40 денежных единиц. Оборудование должно быть размещено на площади, не превышающей 100 кв. м. Предприниматель может заказать оборудование трех типов, стоимость, занимаемая производственная площадь и производительность которых приведены в таблице:
4. Задачи нелинейного программирования
В оптимизационных задачах нелинейного программирования (НЛП) математические модели содержат нелинейные зависимости от переменных. Источники нелинейности относятся в основном к одной из двух категорий:
1) реально существующие и эмпирически наблюдаемые нелинейные соотношения, например: непропорциональные зависимости между объемом производства и затратами; между количеством используемого в производстве компонента и некоторыми показателями качества готовой продукции; между затратами сырья и физическими параметрами (давление, температура и т.п.) соответствующего производственного процесса; между выручкой и объемом реализации и др.;
2) установленные (постулируемые) руководством правила поведения или задаваемые зависимости, например: формулы или правила расчета с потребителями энергии или других видов услуг; эвристические правила определения страховых уровней запаса продукции; гипотезы о характере вероятностного распределения рассматриваемых в модели случайных величин и др.
В отличие от задач линейного программирования, любая из которых может быть решена симплекс-методом, не существует одного или нескольких алгоритмов, эффективных для решения любых нелинейных задач. Эффективность алгоритма может даже существенно зависеть от постановки задачи, например, от изменения масштабов измерения тех или иных переменных. Поэтому алгоритмы разрабатываются для каждого класса (типа) задач.
4.1. Пример решения задачи нелинейного программирования в Mathcad
Для решения задач оптимизации используется блок решения, начинающийся словом Given (дано). До этого ключевого слова должны быть определены начальные значения переменных и целевая функция. После слова Given формируется система ограничений на переменные задачи.
Для задач оптимизации имеются функции Minimize(f, х, у …) и Maximize(f‘, х, у…), решающие задачи минимума и максимума соответственно, где f – оптимизируемая функция, остальные параметры — переменные этой функции.
Пример задачи. Известен рыночный спрос на определенное изделие в количестве 180 штук. Это изделие может быть изготовлено двумя предприятиями по различным технологиям. При производстве первым предприятием его затраты составят руб., а при изготовлении изделий вторым предприятием они составят руб. Определить сколько изделий, изготовленных по каждой технологии, может предложить концерн, чтобы общие издержки его производства были минимальными. Решить задачу средствами Mathcad.
Протокол решения задачи в Mathcad приведен ниже.
Общие затраты на производство
Ответ. На первом предприятии надо произвести 91 изделие, на втором предприятии — 89 изделий.
Задание 4. Решить задачу нелинейного программирования в Mathcad.
Варианты 1-5. Известен рыночный спрос на определенное изделие в количестве N штук. Это изделие может быть изготовлено двумя предприятиями по различным технологиям. При производстве первым предприятием его затраты составят F руб., а при изготовлении изделий вторым предприятием они составят G руб. Определить сколько изделий, изготовленных по каждой технологии, может предложить концерн, чтобы общие издержки его производства были минимальными.
3.2. Пример решения задачи целочисленного линейного программирования в Mathcad
Предприниматель для приобретения оборудования выделяет 40 денежных единиц. Оборудование должно быть размещено на площади, не превышающей 100 кв. м. Предприниматель может заказать оборудование трех типов, стоимость, занимаемая производственная площадь и производительность которых приведены в таблице:
Составить оптимальный план приобретения оборудования, обеспечивающий максимальную общую производительность при условии, что количество единиц 1-го типа оборудования должно быть не меньше, чем количество единиц 2-го типа.
Построим математическую модель задачи. Обозначим через , количество единиц оборудования соответственно 1, 2 и 3 типа. Математическая модель задачи примет вид:
Это задача целочисленного линейного программирования. Найдем решение задачи средствами Mathcad. Будем использовать средства программирования пакета Mathcad для реализации метода полного или сплошного перебора. Для этого определим пределы изменения переменных. Из ограничений получим, что , а
Протокол решения задачи в Mathcad приведен ниже.

Ответ. Максимальную производительность 80 можно получить приобретением 2 единиц 1-го типа оборудования и 5 единиц 3-го типа оборудования.
Задание 3.
Построить математическую модель задачи. Решить задачу целочисленного линейного программирования средствами Mathcad.
Вариант 1. Для приобретения оборудования выделено 34 ден. ед. Оборудование должно быть размещено на площади, не превышающей 60 кв. м. Можно заказать оборудование двух видов: менее мощные машины типа А стоимостью 3 ден. ед, требующие производственную площадь 3 кв. м (с учетом проходов) и обеспечивающие производительность за смену 200 единиц продукции, и более мощные машины типа В стоимостью 4 ден.ед., занимающие площадь 5 кв.м. и обеспечивающие производительность за смену 300. Требуется составить оптимальный план приобретения оборудования, обеспечивающий максимальную общую производительность при условии, что фермер может приобрести не более 8 машин типа В.
Вариант 2. Для приобретения оборудования выделено 38 ден. ед. Оборудование должно быть размещено на площади, не превышающей 50 кв. м. Можно заказать оборудование двух видов: менее мощные машины типа А стоимостью 3 ден. ед, требующие производственную площадь 3 кв. м (с учетом проходов) и обеспечивающие производительность за смену 150 единиц, и более мощные машины типа В стоимостью 4 ден.ед., занимающие площадь 4 кв.м. и обеспечивающие производительность за смену 100. Требуется составить оптимальный план приобретения оборудования, обеспечивающий максимальную общую производительность при условии, что фермер может приобрести не более 8 машин типа В.
Вариант 3. Для приобретения оборудования выделено 40 ден. ед. Оборудование должно быть размещено на площади, не превышающей 60 кв. м. Можно заказать оборудование двух видов: менее мощные машины типа А стоимостью 3 ден. ед, требующие производственную площадь 4 кв. м (с учетом проходов) и обеспечивающие производительность за смену 120 единиц, и более мощные машины типа В стоимостью 4 ден.ед., занимающие площадь 5 кв.м. и обеспечивающие производительность за смену 130. Требуется составить оптимальный план приобретения оборудования, обеспечивающий максимальную общую производительность при условии, что можно приобрести не более 8 машин типа В.
Варианты 4-10. Предприниматель для приобретения оборудования выделяет С денежных единиц. Оборудование должно быть размещено на площади, не превышающей S кв. м. Предприниматель может заказать оборудование трех типов, стоимость, занимаемая производственная площадь и производительность которых приведены в таблице. Составить оптимальный план приобретения оборудования, обеспечивающий максимальную общую производительность при условии, что количество единиц 1-го типа оборудования должно быть не меньше, чем количество единиц 2-го типа.