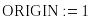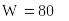Mathcad решение задачи линейного программирования графическим методом

Графический метод решения задачи линейного программирования с использованием системы Mathcad

В работе предлагается при решении задачи линейного программирования графическим методом использовать средства интегрированной системы MATHCAD.

Одной из важнейших задач, стоящих перед высшей школой, является формирование всесторонне образованного специалиста, умеющего применять полученные знания в различных областях инженерной деятельности. В этой связи использование такого средства, как математическая интегрированная система MATHCAD, является мощным инструментом для решения многих практических задач.

При изучении таких дисциплин, как «Прикладная математика», «Математическое обеспечение технологических процессов» и др. рассматривается задача линейного программирования и ее решение графическим методом в двумерном пространстве. Трудно переоценить значение этого метода, позволяющего наглядно представить полученный результат. Реализуется графический метод практически всегда «вручную».

Ниже приводится пример[1,4] графического решения задачи линейного

программирования с использованием средств интегрированной системы MATHCAD.

Постановка одной из прикладных задач. Для изготовления двух видов продукции Р1 и Р2 используют 3 вида сырья: Sj, S2 и S3 .

Запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также величина прибыли, получаемая от реализации единицы продукции, записаны в постановке задачи линейного программирования, где xi — количество единиц продукции Pi, x2 — количество единиц продукции P2, z- функция цели.

Пусть математическая модель задачи имеет вид:

Найти максимум целевой функции z= x1 + 2×2

при заданных ограничениях:

Xi — X2 < 5 15x1 + 4x2 >132 8×1 +11 x2 < 230 xi >0, x2 > 0.

Источник

Mathcad решение задачи линейного программирования графическим методом

БлогNot. Решение задачи линейного программирования графическим методом — как проиллюстрир.

Решение задачи линейного программирования графическим методом — как проиллюстрировать в Mathcad?

Теория приведена, например, здесь (лекция 3). Отметим, что простейшим графическим методом решается задача только для двух неизвестных с линейной целевой функцией. Но рисовать на бумаге, что вышло, мне лично было бы лень.

Можно сделать похитрее и поавтоматизированней, чем в примере, например, попытаться автоматически штриховать область допустимых решений (ОДР), но не будем усложнять простую вещь.

Вот каким алгоритмом сделать понятнее всего. Возьмём классическую задачу линейного программирования (ЛП):

постановка задачи

Ограничения на неотрицательность x1 , x2 тривиальны, а остальные определим как функции 2 переменных r1 , r2 , r3 . Для построения графиков прямых, соответствующих этим трём ограничениям, решим их относительно переменной x2 как равенства, получатся функции f1(x1) , . f3(x1) :

представление ограничений задачи ЛП как уравнений прямых в Mathcad

Целевую функцию зададим как z(x1,x2) , определим для неё 2 любых различных тестовых значения, Level1 и Level2 . Они понадобятся, чтобы увидеть на графике направление возрастания функции (вектор градиента, перпендикулярный обеим линиям и направленный от z(x1,x2)=Level1 к z(x1,x2)=Level2) :

определение целевой функции для задачи ЛП в Mathcad

Чтобы было наглядней, переберём попарно комбинации ограничений-прямых f1 , f2 , f3 и подготовим точки их пересечения P12 , P13 , P23 для отображения на графике:

точки пересечения прямых, соответствующих ограничениям задачи ЛП

Следующий этап, на самом деле, будет выполнен после построения графика — нужно подобрать подходящий для отображения области допустимых решений интервал [a,b] по оси X , а также любую точку Seed , лежащую внутри многоугольника, образованного всеми прямыми-ограничениями. Затем для надёжности проверим, все ли ограничения неравенства выполняются внутри многоугольника ОДР. Если что-то не выполняется, исходное неравенство даст значение не 1, а 0, значит, нужно штриховать противоположную от Seed сторону прямой, многоугольник ОДР окажется разомкнутым. Это ещё не значит, что решения нет, подробнее см. в лекции по первой ссылке:

проверка выполнения исходных ограничений по тестовой точке, лежащей внутри ОДР

Всё готово для построения графика, вот каким наглядным он может быть:

графическое решение задачи ЛП в Mathcad

На первой вкладке свойств графика (войти в это окно можно двойным щелчком по графику) выставлены линии сетки, флажок «В одинаковом масштабе» и опция «Отображение осей по центру». Вторую вкладку («Трассировка») пришлось настроить детальней: кривые 1 и 2 — красные линии, с толщиной 1 и 2 соответственно, чтобы было видно направление градиента. Если бы задача была на минимум, нужно было бы двигаться перпендикулярно красным линиям от толстой к тонкой, у нас максимум, значит — от тонкой к толстой. Кривые 3-5 — чёрные линии, они соответствуют нашим трём ограничениям. Графики 6-8 — точки с символом «кружок» размером 3, они покажут углы многоугольника ОДР. График 9 тоже точка, она изображена фиолетовым квадратиком и контролирует, правильно ли мы выбрали Seed . По графику видно, что решение — точка P13 = (2,3) .

23.12.2015, 00:12 [14005 просмотров]

Источник

Решение задачи линейного программирования в среде Mathcad

Одним из способов решения подобных задач в Mathcad является использование блока given с функциями Minimize и Maximize (пишутся с заглавной буквы).

Описание алгоритма решения задачи

• Построение математической модели задачи

Пусть x_t = (*i, *₂) — количество выпускаемых моделей столов офисных и детских соответственно.

В этой связи целевая функция, в соответствии с формулой (6.4), будет иметь вид:

Имеющиеся ограничения по объёмам сырья: для производства обоих видов столов расходуется 80 м 3 древесины лиственных пород, 40 м 3 древесины хвойных пород и 2800 шт. крепежных элементов.

Запишем имеющееся ограничение по хвойной древесине:

Запишем имеющееся ограничение по лиственной древесине:

Запишем имеющееся ограничение по крепежным элементам:

Получим систему линейных уравнений (ограничений):

• Представление и ввод данных в Mathcad

Специальной переменной ORIGIN присваиваем значение, равное 1. Значением ORIGIN задается номер первого элемента строки или столбца в матрице. По умолчанию ORIGIN=0.

Введем исходные данные задачи в матричной форме.

Зададим количество элементов решения п := 2

Вводим исходные данные задачи в матричной форме, представив коэффициенты при неизвестных в виде матрицы а (в Mathcad целая часть числа отделяется точкой, а не запятой):

Коэффициенты правой части системы уравнений представим в виде матрицы Ь:

Коэффициенты с целевой функции /(*) представим в виде матрицы с:

Представим целевую функцию в общем виде:

Зададим начальные значения искомых (управляемых) переменных:

Используем блок given для задания имеющихся ограничений в Matcad:

Зададим ограничение на то, что переменные, полученные в ходе расчета, должны быть неотрицательны:

Для нахождения корней уравнений, решения задачи, используем функцию Maximize:

Результат расчета будет представлен в виде вектора х (ставим знак равно, а не присвоение):

Результат расчета функции:

На основании выполненных расчетов можно сделать следующий вывод: оптимальным планом для предприятия при имеющихся условиях будет выпуск 25 офисных и 175 детских столов, прибыль от продажи составит 875000 рублей.

Список литературы к разделу

• 6
• 1. Охорзин, В. А. Прикладная математика в системе Mathcad: учеб, пособие для студентов вузов по направлению подготовки дипломированного специалиста 160400 «Системы управления движением и навигации» и специальности 160403 «Системы управления летательными аппаратами» / В. А. Охорзин. — Изд. 3-е, стер. — СПб.: Лань, 2009. — 348 с.: ил.

• 2. Советов, Б. Я. Моделирование систем: учеб, для студентов вузов по направлениям «Информатика и вычислительная техника», «Информационные системы» / Б. Я. Советов, С. А. Яковлев. — 4-е изд., стер. — М.: Высш. шк., 2006. — 342 с.
• 3. By колов, Э. А. Основы статистического анализа: практикум по статистическим методам и исследованию операций с использованием пакетов STATISTIC А и EXCEL: учеб, пособие по специальности «Менеджмент организаций» / Э. А. Вуколов. — 2-е изд., испр. и доп. — М. : ФОРУМ, 2012. — 463 с.

Источник

3.2. Пример решения задачи целочисленного линейного программирования в Mathcad

Предприниматель для приобретения оборудования выделяет 40 денежных единиц. Оборудование должно быть размещено на площади, не превышающей 100 кв. м. Предприниматель может заказать оборудование трех типов, стоимость, занимаемая производственная площадь и производительность которых приведены в таблице:

Составить оптимальный план приобретения оборудования, обеспечивающий максимальную общую производительность при условии, что количество единиц 1-го типа оборудования должно быть не меньше, чем количество единиц 2-го типа.

Построим математическую модель задачи. Обозначим через , количество единиц оборудования соответственно 1, 2 и 3 типа. Математическая модель задачи примет вид:

Это задача целочисленного линейного программирования. Найдем решение задачи средствами Mathcad. Будем использовать средства программирования пакета Mathcad для реализации метода полного или сплошного перебора. Для этого определим пределы изменения переменных. Из ограничений получим, что , а

Протокол решения задачи в Mathcad приведен ниже.

Ответ. Максимальную производительность 80 можно получить приобретением 2 единиц 1-го типа оборудования и 5 единиц 3-го типа оборудования.

Задание 3.

Построить математическую модель задачи. Решить задачу целочисленного линейного программирования средствами Mathcad.

Вариант 1. Для приобретения оборудования выделено 34 ден. ед. Оборудование должно быть размещено на площади, не превышающей 60 кв. м. Можно заказать оборудование двух видов: менее мощные машины типа А стоимостью 3 ден. ед, требующие производственную площадь 3 кв. м (с учетом проходов) и обеспечивающие производительность за смену 200 единиц продукции, и более мощные машины типа В стоимостью 4 ден.ед., занимающие площадь 5 кв.м. и обеспечивающие производительность за смену 300. Требуется составить оптимальный план приобретения оборудования, обеспечивающий максимальную общую производительность при условии, что фермер может приобрести не более 8 машин типа В.

Вариант 2. Для приобретения оборудования выделено 38 ден. ед. Оборудование должно быть размещено на площади, не превышающей 50 кв. м. Можно заказать оборудование двух видов: менее мощные машины типа А стоимостью 3 ден. ед, требующие производственную площадь 3 кв. м (с учетом проходов) и обеспечивающие производительность за смену 150 единиц, и более мощные машины типа В стоимостью 4 ден.ед., занимающие площадь 4 кв.м. и обеспечивающие производительность за смену 100. Требуется составить оптимальный план приобретения оборудования, обеспечивающий максимальную общую производительность при условии, что фермер может приобрести не более 8 машин типа В.

Вариант 3. Для приобретения оборудования выделено 40 ден. ед. Оборудование должно быть размещено на площади, не превышающей 60 кв. м. Можно заказать оборудование двух видов: менее мощные машины типа А стоимостью 3 ден. ед, требующие производственную площадь 4 кв. м (с учетом проходов) и обеспечивающие производительность за смену 120 единиц, и более мощные машины типа В стоимостью 4 ден.ед., занимающие площадь 5 кв.м. и обеспечивающие производительность за смену 130. Требуется составить оптимальный план приобретения оборудования, обеспечивающий максимальную общую производительность при условии, что можно приобрести не более 8 машин типа В.

Варианты 4-10. Предприниматель для приобретения оборудования выделяет С денежных единиц. Оборудование должно быть размещено на площади, не превышающей S кв. м. Предприниматель может заказать оборудование трех типов, стоимость, занимаемая производственная площадь и производительность которых приведены в таблице. Составить оптимальный план приобретения оборудования, обеспечивающий максимальную общую производительность при условии, что количество единиц 1-го типа оборудования должно быть не меньше, чем количество единиц 2-го типа.

Источник