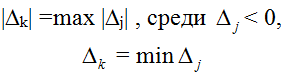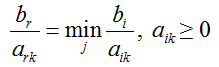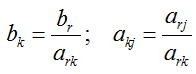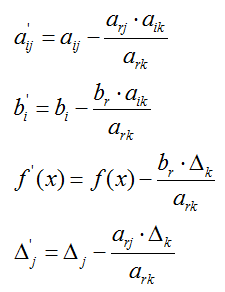Код java симплекс метод

Программирование на C, C# и Java

Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы

ОСТОРОЖНО МОШЕННИКИ! В последнее время в социальных сетях участились случаи предложения помощи в написании программ от лиц, прикрывающихся сайтом vscode.ru. Мы никогда не пишем первыми и не размещаем никакие материалы в посторонних группах ВК. Для связи с нами используйте исключительно эти контакты: vscoderu@yandex.ru, https://vk.com/vscode

Симплекс-метод. Реализация

В этой статье рассматривается симплекс-метод, который применяется при решении задач линейного программирования (ЗЛП). Приводится алгоритм метода, а также его реализация на языке C#. Реализация представлена в конце статьи.

Определения

Симплекс-метод — это алгоритм, используемый при решении оптимизационной задачи линейного программирования.

Линейное программирование — это раздел математики, занимающийся решением экстремальных задач (нахождением экстремума функции) на множестве пространства, заданном системой линейных уравнений и неравенств.

Оптимизация — задача нахождения минимума или максимума (экстремума) целевой функции.

Целевая функция — это функция нескольких переменных, подлежащая оптимизации в целях решения какой-либо оптимизационной задачи (например, задачи объемного планирования).

Алгоритм симплекс-метода

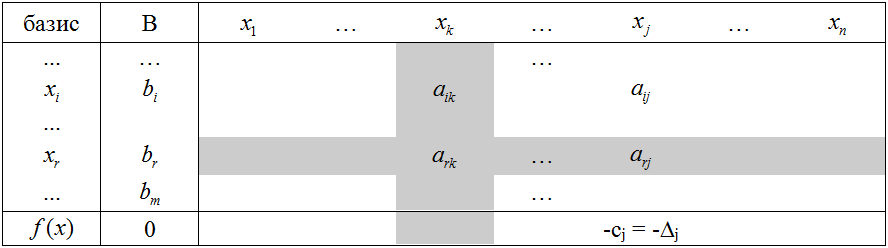
В начале исходную задачу линейного программирования приводят к каноническому виду, затем составляют симплекс-таблицу вида:

где в столбце «базис» указываются базисные переменные, а в последней строке столбца «базис» пишется f(x). В столбец «B» записываются свободные члены ограничений b_i и значение целевой функции (на 1-м этапе оно равно 0, т.е. никакой прибыли).

В столбцах x_j для не базисных переменных указываются коэффициенты при не базисных переменных из ограничений задачи. В столбцах базисных переменных содержится только 0 или 1 на пересечении столбца с соответствующей строкой базисной переменной.

В последней строке -c_j — это коэффициенты при переменных целевой функции взятые с противоположным знаком.

Симплекс-таблица составлена, теперь опишем сам симплекс-метод.

Шаг 1: Выполняется проверка полученного базисного плана на оптимальность по условию: если при каком-либо ДБР (допустимое базисное решение) в симплекс-таблице все коэффициенты строки f(x) (то есть -c_j) не отрицательны, то данное ДБР оптимально, следовательно КОНЕЦ решения. В противном случае:

Шаг 2: Переход к новому базисному плану. Для этого из числа небазисных переменных с отрицательными значениями в последней строке (то есть -c_j < 0) выбирается переменная, вводимая в базис — x_k, это переменная которой соответствует наибольшая по модулю отрицательная оценка:

Столбец, отвечающий переменной x_k, называется главным, или ведущим. Элементы данного столбца обозначаются через a_ik.

Если окажется несколько одинаковых наибольших по модулю отрицательных оценок, то выбирается любая из соответственных переменных.

Шаг 3: Выбираем переменную r — переменную, которая выводится из базиса. Данная переменная находится из соотношения:

Строка таблицы, в которой получено наименьшее отношение элемента столбца «В» к соответствующему положительному элементу ведущего столбца, является ведущей, или главной.

Элементы главной строки обозначаются через a_rj. Выбранная переменная x_r будет выводиться из базиса, то есть это исключаемая переменная.

Если окажется несколько одинаковых наименьших значений отношений, то выбирается любая из соответствующих им переменных.

Элемент, который стоит на пересечении главного столбца и строки называется главным, или ведущим, и обозначается a_rk.

Шаг 4: Для определения нового базисного плана проводится пересчет элементов симплекс-таблицы, и результаты заносятся в новую таблицу. Выбранные переменные среди базисных и не базисных, лежащих на главной строке и главном столбце, меняются местами.

Процедура пересчета элементов выполняется следующим образом:

а) элементы главной строки необходимо разделить на ведущий элемент:

б) элементы полученной строки умножаются на -a_ik, и результаты складываются с i-той строкой, причем i ≠ k:

После определения новой симплекс-таблицы переходят к шагу 1.

Симплекс-метод. Реализация C#

Приводим программную реализацию симплекс-метода. Программа написана на языке программирования C#.

Важная информация! Пожалуйста прочтите!

Входные данные: симплекс-таблица без базисных переменных в столбцах. То есть таблица должна быть построена только по коэффициентам при переменных из ограничений задачи и целевой функции.

Формат входных данных: двумерный массив из элементов типа double.

Входные данные передаются в качестве аргумента, при создании экземпляра класса Simplex.

При вызове метода Calculate в качестве аргумента вы должны передать одномерный массив из элементов типа double, длиной в количество переменных в целевой функции. В этот массив будут записаны найденные значения неизвестных.

Выходные данные: метод Calculate возвращает ссылку на двумерный массив, содержащий решенную симплекс-таблицу. Кроме того решение будет занесено в массив, переданный в качестве аргумента в метод Calculate.

Формат выходных данных: двумерный массив из элементов типа double и одномерный массив из элементов типа double.

Источник

Jason’s Blog

Simplex is one of the powerful algorithm to solve linear programming problems. With simplex, we can maximise or minimise objective function with the given list of constraint.

System.out.println(«M font-family: Monaco; font-size: 11px;»> System.out.println(«N font-family: Monaco; font-size: 11px;»> for (int i = 0; i

System.out.println(«value font-family: Monaco; font-size: 11px;»> for (int i = 0; i < numberOfConstraints; i++)

System.out.println(«x[» + i + «] font-family: Monaco; font-size: 11px;»> System.out.println(«Solution: » + simplex.value());

• Get link
• Facebook
• Twitter
• Pinterest
• Email
• Other Apps

Comments

hi Jason, I’m Yulius. I want to ask about your code in above. How when I have the constraint is X2 = X1 or Y = X Reply Delete

i am akash.i want to input constraint by user for solving dual simplex and output in the table form plzzz sir give me source code of this.
Reply Delete

I think the -z row(last row) is wrong, the equation function is not obtained through Gauss-Jordan elimination. Reply Delete

when i tried running the code. i got an errror saying.
C:\JAVACOURSEMAIN\LectureElements\simplex.java:3: error: class Simplex is public, should be declared in a file named Simplex.java
public class Simplex ^
1 error

Tool completed with exit code 1
Reply Delete

Источник

mik30s / SimplexClass.java

This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters

// The Following solves a linear programming problem

// In standardized form using the simplex method

// Please the read below.

/************************************************USAGE*************************************************************

* 1.Create an instance of the simplex class

* 2.Fill in the table with the standardized form of the problem by calling simplex.fillTable()

* 3.Create a while loop and call the simplex.compute() method until it returns ERROR.IS_OPTIMAL or ERROR.UNBOUNDED

* ****************************************************************************************************************/

public class Simplex

private int rows , cols ; // row and column

private float [][] table ; // simplex tableau

private boolean solutionIsUnbounded = false ;

public static enum ERROR

NOT_OPTIMAL ,

IS_OPTIMAL ,

UNBOUNDED

>;

public Simplex ( int numOfConstraints , int numOfUnknowns )

rows = numOfConstraints + 1 ; // row number + 1

cols = numOfUnknowns + 1 ; // column number + 1

table = new float [ rows ][]; // create a 2d array

// initialize references to arrays

for ( int i = 0 ; i < rows ; i ++)

table [ i ] = new float [ cols ];

>

>

// prints out the simplex tableau

public void print ()

for ( int i = 0 ; i < rows ; i ++)

for ( int j = 0 ; j < cols ; j ++)

String value = String . format ( «%.2f» , table [ i ][ j ]);

System . out . print ( value + » \t » );

>

System . out . println ();

>

System . out . println ();

>

// fills the simplex tableau with coefficients

public void fillTable ( float [][] data )

for ( int i = 0 ; i < table . length ; i ++)

System . arraycopy ( data [ i ], 0 , this . table [ i ], 0 , data [ i ]. length );

>

>

// computes the values of the simplex tableau

// should be use in a loop to continously compute until

// an optimal solution is found

public ERROR compute ()

// step 1

if ( checkOptimality ())

return ERROR . IS_OPTIMAL ; // solution is optimal

>

// step 2

// find the entering column

int pivotColumn = findEnteringColumn ();

System . out . println ( «Pivot Column: » + pivotColumn );

// step 3

// find departing value

float [] ratios = calculateRatios ( pivotColumn );

if ( solutionIsUnbounded == true )

return ERROR . UNBOUNDED ;

int pivotRow = findSmallestValue ( ratios );

//System.out.println(«Pivot row: «+ pivotRow);

// step 4

// form the next tableau

formNextTableau ( pivotRow , pivotColumn );

// since we formed a new table so return NOT_OPTIMAL

return ERROR . NOT_OPTIMAL ;

>

// Forms a new tableau from precomuted values.

private void formNextTableau ( int pivotRow , int pivotColumn )

float pivotValue = table [ pivotRow ][ pivotColumn ];

float [] pivotRowVals = new float [ cols ];

float [] pivotColumnVals = new float [ cols ];

float [] rowNew = new float [ cols ];

// divide all entries in pivot row by entry inpivot column

// get entry in pivot row

System . arraycopy ( table [ pivotRow ], 0 , pivotRowVals , 0 , cols );

// get entry inpivot colum

for ( int i = 0 ; i < rows ; i ++)

pivotColumnVals [ i ] = table [ i ][ pivotColumn ];

// divide values in pivot row by pivot value

for ( int i = 0 ; i < cols ; i ++)

rowNew [ i ] = pivotRowVals [ i ] / pivotValue ;

// subtract from each of the other rows

for ( int i = 0 ; i < rows ; i ++)

if ( i != pivotRow )

for ( int j = 0 ; j < cols ; j ++)

float c = pivotColumnVals [ i ];

table [ i ][ j ] = table [ i ][ j ] — ( c * rowNew [ j ]);

>

>

>

// replace the row

System . arraycopy ( rowNew , 0 , table [ pivotRow ], 0 , rowNew . length );

>

// calculates the pivot row ratios

private float [] calculateRatios ( int column )

float [] positiveEntries = new float [ rows ];

float [] res = new float [ rows ];

int allNegativeCount = 0 ;

for ( int i = 0 ; i < rows ; i ++)

if ( table [ i ][ column ] > 0 )

positiveEntries [ i ] = table [ i ][ column ];

>

else

positiveEntries [ i ] = 0 ;

allNegativeCount ++;

>

//System.out.println(positiveEntries[i]);

>

if ( allNegativeCount == rows )

this . solutionIsUnbounded = true ;

else

for ( int i = 0 ; i < rows ; i ++)

float val = positiveEntries [ i ];

if ( val > 0 )

res [ i ] = table [ i ][ cols — 1 ] / val ;

>

>

>

return res ;

>

// finds the next entering column

private int findEnteringColumn ()

float [] values = new float [ cols ];

int location = 0 ;

int pos , count = 0 ;

for ( pos = 0 ; pos < cols - 1 ; pos ++)

if ( table [ rows — 1 ][ pos ] < 0 )

//System.out.println(«negative value found»);

count ++;

>

>

if ( count > 1 )

for ( int i = 0 ; i < cols - 1 ; i ++)

values [ i ] = Math . abs ( table [ rows — 1 ][ i ]);

location = findLargestValue ( values );

> else location = count — 1 ;

return location ;

>

// finds the smallest value in an array

private int findSmallestValue ( float [] data )

float minimum ;

int c , location = 0 ;

minimum = data [ 0 ];

for ( c = 1 ; c < data . length ; c ++)

if ( data [ c ] > 0 )

if ( Float . compare ( data [ c ], minimum ) < 0 )

minimum = data [ c ];

location = c ;

>

>

>

return location ;

>

// finds the largest value in an array

private int findLargestValue ( float [] data )

float maximum = 0 ;

int c , location = 0 ;

maximum = data [ 0 ];

for ( c = 1 ; c < data . length ; c ++)

if ( Float . compare ( data [ c ], maximum ) > 0 )

maximum = data [ c ];

location = c ;

>

>

return location ;

>

// checks if the table is optimal

public boolean checkOptimality ()

boolean isOptimal = false ;

int vCount = 0 ;

for ( int i = 0 ; i < cols - 1 ; i ++)

float val = table [ rows — 1 ][ i ];

if ( val >= 0 )

vCount ++;

>

>

if ( vCount == cols — 1 )

isOptimal = true ;

>

return isOptimal ;

>

// returns the simplex tableau

public float [][] getTable ()

return table ;

>

>

Источник