Рекурсия в Java: пример программы + детальный обзор
В языке Java поддерживается рекурсия — процесс определения чего-либо относительно самого себя.
Применительно к программированию на Java рекурсия — это средство, которое позволяет методу вызывать самого себя. Такой метод называется рекурсивным.
Классическим примером рекурсии служит вычисление факториала числа. Факториал числа N — это произведение всех целых чисел от 1 до N. Например ,факториал числа 3 равен 1 х 2 х 3, т.е. 6. Ниже показано, как вычислить факториал, используя рекурсивный метод.
Ниже приведен результат, выводимый этой программой.
Тем, кто незнаком с рекурсивными методами, принцип действия метода fact() может быть не совсем понятным.
Метод fact() действует следующим образом. Когда этот метод вызывается со значением 1 своего аргумента, возвращается значение 1. В противном случае возвращается произведение fact(n — 1) * n .
Для вычисления этого выражения метод fact() вызывается со значением n — 1 своего аргумента. Этот процесс повторяется до тех пор, пока n не станет равным 1, после чего начнется возврат из последовательных вызовов метода fact().
Для того чтобы стал понятнее принцип действия рекурсивного метода fact(), обратимся к небольшому примеру.
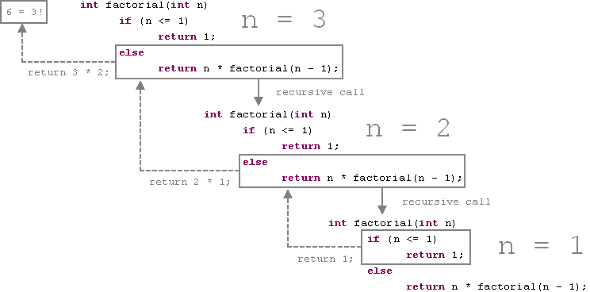
Для расчета факториала числа З вслед за первым вызовом метода fact() происходит второй вызов этого метода со значением 2 его аргумента.
Это, в свою очередь, приводит к третьему вызову метода fact() со значением 1 его аргумента. Возвращаемое из этого вызова значение 1 затем умножается на 2 (т.е. значение n при втором вызове метода).
Полученный результат ,равный 2 , возвращается далее исходному вызову метода fact() и умножается на 3 (исходное значение n).
В конечном итоге получается искомый результат, равный 6. В метод fact() можно было бы ввести вызовы метода println(), чтобы отображать уровень каждого вызова и промежуточные результаты вычисления факториала заданного числа.
Когда рекурсивный метод вызывает самого себя, новым локальным переменными параметрам выделяется место в стеке и код метода выполняется с этими новыми исходными значениями.
При каждом возврате из вызова рекурсивного методапрежние локальные переменные и параметры удаляются из стека, а выполнение продолжается с точки вызова в самом методе.
Рекурсивные методы выполняют действия, которые можно сравнить с раскладыванием и складыванием телескопа.
Вследствие издержек на дополнительные вызовы рекурсивные варианты многих процедур могут выполняться медленнее их итерационных аналогов.
Слишком большое количество вызовов рекурсивного метода может привести к переполнению стека, поскольку параметры и локальные переменные сохраняются в стеке, а при каждом новом вызове создаются новые копии этих значений.
В таком случаев исполняющей системе Jаvа возникнет исключение. Но подобная ситуация не возникнет, если не выпустить рекурсивный метод из-под контроля.
Главное преимущество рекурсивных методов заключается в том, что их можно применять для реализации более простых и понятных вариантов некоторых алгоритмов, чем их итерационные аналоги.
Например, алгоритм быстрой сортировки очень трудно реализовать итерационным способом. А некоторые виды алгоритмов, связанных с искусственным интеллектом, легче всего реализовать с помощью рекурсивных решений.
При написании рекурсивных методов следует позаботиться о том, чтобы в каком нибудь другом месте программы присутствовал условный оператор if, осуществляющий возврат из метода без его рекурсивного вызова.
В противном случае возврата из рекурсивно вызываемого метода так и не произойдет. Подобная ошибка очень часто встречается при организации рекурсии.
Поэтому на стадии разработки рекурсивных методов рекомендуется как можно чаще делать вызовы метода println(), чтобы следить за происходящим и прерывать выполнение при обнаружении ошибки.
Рассмотрим еще один пример организации рекурсии. В данном примере рекурсивный метод рrintArrау() выводит первые i элементов из массива values.
Рекурсия в Java
Чтобы понять, что такое рекурсия, нужно понять, что такое рекурсия. На самом деле, в понимании таких функций нет ничего сложного, нужно только один раз хорошо в этом разобраться. И попрактиковаться, если речь идёт о программировании. Рекурсия встречается не только в программировании, но и в реальной жизни. Возьми в руки зеркало и встань напротив другого зеркала. Отражение отражения отразится в отражении и так далее. Ты увидишь бесконечное количество отражений, уходящих в бесконечность. Больше о “реальной” рекурсии ты можешь найти в статье “Дню Сурка посвящается…” Возвратимся из реального мира к будням программиста. Простое определение: рекурсивные функции в java – это функции, которые вызывают сами себя. Приведу очень простой и очень вредный пример:
public void recursionFucn()
- Базис рекурсии – условие выхода из блока рекурсивных вызовов – базисное решение задачи, при условиях, когда нет необходимости вызывать рекурсию.
- Шаг рекурсии – вызов функцией самой себя при изменении параметров.
private int fact(int n) < int result = 1; for (int i = 1; i return result; > private int fact(int n) < if (n < 0) < System.out.println("Зачем тебе факториал из отрицательного числа?"); return null; >int result = 1; if (n == 0) < return result; >for (int i = 1; i return result; > private int factorial(int n) < int result = 1; if (n == 1 || n == 0) < return result; >result = n * factorial(n-1); return result; > System.out.println(factorial(0)); System.out.println(factorial(1)); System.out.println(factorial(2)); System.out.println(factorial(3)); System.out.println(factorial(4)); System.out.println(factorial(5)); System.out.println(factorial(6)); private int factorial(int n) < int result = 1; if (n == 0) < System.out.print(" = "); return result; >if (n == 1) < System.out.print(" * 1 = "); return result; >System.out.print(n); if (n != 2) < System.out.print(" * "); >result = n * factorial(n-1); return result; > System.out.println(factorial(15) + "!"); Получим: 15 * 14 * 13 * 12 * 11 * 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 1 307 674 368 000! В данном случае применение рекурсивной функции оправдано и безопасно. Мы четко обозначили условие выхода из рекурсивного блока, и мы уверены в том, что он достижим: мы вводим целое неотрицательное число, в случае, если число равно нулю или единице — возвращаем результат, если же число больше — умножаем результат на функцию от числа n-1 . На примере факториала от трех:
factorial(3) внутри себя выполнит следующее: result = 3 * factorial(2); (рекурсивный вызов) factorial(2) внутри себя выполнит следующее: result = 2 * factorial(1); (рекурсивный вызов) factorial(1) вернет 1 (базис рекурсии) factorial(2) вернет 2 * 1 factorial(3) вернет 3 * 2 * 1 По поводу осторожности применения: в чем уязвимость этой функции? Если дать методу в качестве параметра отрицательное число, то проверка
не имеет смысла и мы уйдем в бесконечный цикл вызовов методом самого себя. Стоит добавить проверку на неотрицательность:
В чем преимущество одного метода перед другим? Кажется, что большой разницы нет, но на самом деле множество рекурсивных вызовов негативно скажется на производительности и потребляемой памяти: стек вызовов – практически неконтролируемый ресурс и при разных условиях вызова одной и той же рекурсивной функции, мы можем получить или не получить проблемы, связанные с этим ресурсом. Практически все задачи, решаемые с помощью итераций (циклов типа for-each ), можно решить и рекурсивно. Преимущество рекурсии в читаемости и простоте написания, о недостатках мы говорили выше: возможность «выстрелить себе в ногу» неиллюзорна. Еще более осторожным надо быть при использовании так называемой «сложной рекурсии»: Функция A() вызовет функцию B() , вызывающую функцию A() .Для решения таких задач необходимо полное понимание того, как работает рекурсия. Пример такой задачи: вычисление значения x^n/(n!) . Факториал, как мы обсуждали выше, определен на множестве неотрицательных целых чисел. Напоследок приведу код решения. Сложная рекурсия будет состоять из двух методов:
private double calculate(int x, int n) < return power(x, n) / n; >private double power(int x, int n)
Для входа в рекурсию используется метод calculate , вызывающий метод power , в свою очередь вызывающий метод calculate . Базис рекурсии мы обозначили в методе power:
return x * calculate(x, n - 1); - Любое число, кроме нуля, в нулевой степени равно 1 . Если n = 0 , то n! = 1 . Нужно вернуть 1 .
- Нуль в любой степени равен нулю.
- Неопределенность типа 0^0 рассматривать не будем и примем такие входные данные за невалидные.
private double calculate(int x, int n) throws ArithmeticException < if (x == 0 && n == 0) < throw new ArithmeticException("Невалидные входные данные: Неопределенность типа 0^0"); >if (n < 0) < throw new ArithmeticException("Невалидные входные данные: Факториал из отрицательного числа!"); >if (n == 0) < return 1; >if (x == 0) < return 0; >if (x == 0) < return 0; >return power(x, n) / n; > private double power(int x, int n) try < System.out.println(calculate(x, n)); >catch (ArithmeticException e)
В двух словах о рекурсии
public class Recursion < public static void main(String[] args) < System.out.println("Изначальный REC ( 15 , 9 )" ); System.out.println(rec(15,9)); // запускаем sout с возвращаемым функцией [rec] результатом >static int rec (int m, int n) < // передаем в функцию [rec] 2 числа if(m % n == 0) < // если первое число [m] делится на второе число [n] нацело, то возвращаем его System.out.println("Окончателное число " + n); return n; >else < // если не делится нацело, то перезапускаем функцию и заносим в него другие аргументы : // в качестве первого уже будет второе число [n], // а в качестве второго будет остаток от деления первого[m] на второе[n] 15 / 9 = 1 (+ остаток 6) System.out.println("Заносим в REC (" + n + " , " + m % n + ")"); return rec(n,m % n); >> - Рекурсия в Java — это запуск функции, из самой функции.
- При запуске функции, все что было сделано внутри функции стирается и запускается новая функция, с новыми параметрами.
Не затронуто то, почему рекурсия плоха. Почему можем схватить стэк оверфлоу, с чем связано и как регулируется, на основе каких параметров. Чем заменяется рекурсия? Базовые задачи (числа Фибоначчи), как их лучше сделать (на степике был курс на эту тему + на хабре видел 1 или 2 отличные статьи на тему того, как улучшать такие алгоритмы). Какие прикладные задачи всё таки решаются при помощи рекурсии?
Рекурсия
— Привет, Амиго. Сегодня Билаабо расскажет тебе, что такое рекурсия.

Как ты знаешь, в Java одни методы вызывают другие методы. При этом, при вызове метода, в него передаются конкретные значения аргументов, а во время его работы локальные переменные метода принимают некоторые значения.
— И как ты знаешь, внутренние переменные разных методов независимы друг от друга.
— Так вот, представь ситуацию, когда метод может вызвать сам себя. Именно она называется рекурсией. Пример:
public static void main(String[] args) < countDown(10); > public static void countDown(int x) < if (x <=0) System.out.println("Boom!"); else < System.out.println(x); countDown(x - 1); > >10 9 8 7 6 5 4 3 2 1 Boom!— Честно говоря, вижу, что метод в коде сам себя вызывает, но не понимаю, что именно при этом происходит.
— Да примерно то же, что и при вызове другого метода.
— Нет, я спрашиваю, что происходит с переменными? С их значениями? И как мы выходим из метода? Или мы выходим из всех сразу?
— Господи. Да все гораздо проще. Представь что метод, который вызывает сам себя, размножили много раз. Тогда будет аналогичная ситуация:
public static void main(String[] args) < countDown(3); > public static void countDown(int x) < if (x <=0) System.out.println("Boom!"); else < System.out.println(x); countDown(x - 1); > >public static void main(String[] args) < countDown1(3); > public static void countDown1(int x) < if (x <=0) System.out.println("Boom!"); else < System.out.println(x); countDown2(x - 1); > > public static void countDown2(int x) < if (x <=0) System.out.println("Boom!"); else < System.out.println(x); countDown3(x - 1); > > public static void countDown3(int x) < if (x <=0) System.out.println("Boom!"); else < System.out.println(x); countDown4(x - 1); > > public static void countDown4(int x) < if (x <=0) System.out.println("Boom!"); else < System.out.println(x); countDown5(x - 1); > >Т.е. каждый раз при вызове метода (даже самого себя) создаются новые переменные, которые хранят данные для этого метода. Никаких общих переменных нет.
При каждом вызове в памяти появляется еще одна копия аргументов метода, но уже с новыми значениями. При возвращении в старый метод, там используются его переменные. Т.е. при рекурсии фактически мы вызываем другой метод, но с таким же кодом как наш!
— Ясно. А как работает выход из этих методов? Можно пример?
— Ладно. Один пример стоит тысячи слов. Вот тебе пример:
public static void main(String[] args) < print(3); > public static void print(int x) < if (x <=0) System.out.println("Boom!"); else < System.out.println(x); print(x - 1); System.out.println(x); > >public static void main(String[] args) < print1(3); > public static void print1(int x) < if (x <=0) System.out.println("Boom!"); else < System.out.println(x); print2(x - 1); System.out.println(x); > > public static void print2(int x) < if (x <=0) System.out.println("Boom!"); else < System.out.println(x); print3(x - 1); System.out.println(x); > > …— Ок. Вроде понял. А зачем нужна рекурсия?
— Есть очень много задач, которые разбиваются на отдельные подзадачи, идентичные первоначальной задаче. Например, надо обойти все элементы XML-дерева. У каждого элемента может быть несколько дочерних элементов, а у них — свои.
Или тебе нужно вывести список файлов, которые есть в директории и все ее поддиректориях. Тогда ты пишешь метод, который выводит файлы текущей директории, а потом для получения файлов всех поддиректорий вызываешь его же, но с другим параметром – поддиректорией.
public static void main(String[] args) < printAllFiles(new File("c:/windows/")); > public static void printAllFiles(File dir) < for (File file : dir.listFiles()) < if (file.isDirectory()) printAllFiles(file); else System.out.println(file.getAbsolutePath()); > >Строка 8 – получаем список всех файлов (и директорий) в директории dir.
Строки 10-11 – если файл на самом деле директория, то для вывода ее файлов опять вызываем printAllFiles , но уже с другим параметром – поддиректорией.
Строка 13 – выводим имя текущего файла.
— Ок. Вроде понял. Спасибо, Билаабо.