Graph program in python

Python Patterns — Implementing Graphs

This page stays here for historical reasons and it may contain outdated or incorrect information.

Change notes: 2/22/98, 3/2/98, 12/4/00: This version of this essay fixes several bugs in the code. 6/10/19: Retraction of find_shortest_path as «nearly optimal». 8/11/19: Fix accidental usage of find_graph() instead of find_path()

Copyright (c) 1998, 2000, 2003, 2019 Python Software Foundation. All rights reserved. Licensed under the PSF license.

Graphs are networks consisting of nodes connected by edges or arcs. In directed graphs, the connections between nodes have a direction, and are called arcs; in undirected graphs, the connections have no direction and are called edges. We mainly discuss directed graphs. Algorithms in graphs include finding a path between two nodes, finding the shortest path between two nodes, determining cycles in the graph (a cycle is a non-empty path from a node to itself), finding a path that reaches all nodes (the famous «traveling salesman problem»), and so on. Sometimes the nodes or arcs of a graph have weights or costs associated with them, and we are interested in finding the cheapest path.

There’s considerable literature on graph algorithms, which are an important part of discrete mathematics. Graphs also have much practical use in computer algorithms. Obvious examples can be found in the management of networks, but examples abound in many other areas. For instance, caller-callee relationships in a computer program can be seen as a graph (where cycles indicate recursion, and unreachable nodes represent dead code).

Few programming languages provide direct support for graphs as a data type, and Python is no exception. However, graphs are easily built out of lists and dictionaries. For instance, here’s a simple graph (I can’t use drawings in these columns, so I write down the graph’s arcs):

A -> B A -> C B -> C B -> D C -> D D -> C E -> F F -> C

This graph has six nodes (A-F) and eight arcs. It can be represented by the following Python data structure:

This is a dictionary whose keys are the nodes of the graph. For each key, the corresponding value is a list containing the nodes that are connected by a direct arc from this node. This is about as simple as it gets (even simpler, the nodes could be represented by numbers instead of names, but names are more convenient and can easily be made to carry more information, such as city names).

Let’s write a simple function to determine a path between two nodes. It takes a graph and the start and end nodes as arguments. It will return a list of nodes (including the start and end nodes) comprising the path. When no path can be found, it returns None. The same node will not occur more than once on the path returned (i.e. it won’t contain cycles). The algorithm uses an important technique called backtracking: it tries each possibility in turn until it finds a solution.

def find_path(graph, start, end, path=[]): path = path + [start] if start == end: return path if not graph.has_key(start): return None for node in graph[start]: if node not in path: newpath = find_path(graph, node, end, path) if newpath: return newpath return None

>>> find_path(graph, 'A', 'D') ['A', 'B', 'C', 'D'] >>>

The second ‘if’ statement is necessary only in case there are nodes that are listed as end points for arcs but that don’t have outgoing arcs themselves, and aren’t listed in the graph at all. Such nodes could also be contained in the graph, with an empty list of outgoing arcs, but sometimes it is more convenient not to require this.

Note that while the user calls find_path() with three arguments, it calls itself with a fourth argument: the path that has already been traversed. The default value for this argument is the empty list, ‘[]’, meaning no nodes have been traversed yet. This argument is used to avoid cycles (the first ‘if’ inside the ‘for’ loop). The ‘path’ argument is not modified: the assignment «path = path + [start]» creates a new list. If we had written «path.append(start)» instead, we would have modified the variable ‘path’ in the caller, with disastrous results. (Using tuples, we could have been sure this would not happen, at the cost of having to write «path = path + (start,)» since «(start)» isn’t a singleton tuple — it is just a parenthesized expression.)

It is simple to change this function to return a list of all paths (without cycles) instead of the first path it finds:

def find_all_paths(graph, start, end, path=[]): path = path + [start] if start == end: return [path] if not graph.has_key(start): return [] paths = [] for node in graph[start]: if node not in path: newpaths = find_all_paths(graph, node, end, path) for newpath in newpaths: paths.append(newpath) return paths

>>> find_all_paths(graph, 'A', 'D') [['A', 'B', 'C', 'D'], ['A', 'B', 'D'], ['A', 'C', 'D']] >>>

def find_shortest_path(graph, start, end, path=[]): path = path + [start] if start == end: return path if not graph.has_key(start): return None shortest = None for node in graph[start]: if node not in path: newpath = find_shortest_path(graph, node, end, path) if newpath: if not shortest or len(newpath) < len(shortest): shortest = newpath return shortest

>>> find_shortest_path(graph, 'A', 'D') ['A', 'C', 'D'] >>>

These functions are about as simple as they get. Yet, they are nearly optimal (for code written in Python). In another Python Patterns column, I will try to analyze their running speed and improve their performance, at the cost of more code.

UPDATE: Eryk Kopczyński pointed out that these functions are not optimal. To the contrary, "this program runs in exponential time, while find_shortest_path can be done in linear time using BFS [Breadth First Search]. Furthermore a linear BFS is simpler:"

# Code by Eryk Kopczyński def find_shortest_path(graph, start, end): dist = q = deque(start) while len(q): at = q.popleft() for next in graph[at]: if next not in dist: dist[next] = [dist[at], next] q.append(next) return dist.get(end)

Note that this returns the path in a weird format, e.g., [[['A'], 'B'], 'D'] . In particular, len(find_shortest_path(graph, 'A', 'D')) will give the incorrect answer (2, because the outer list is of length 2). This is because append is done as [dist[at], next] instead of dist[at]+[next] . The second method would use quadratic time and memory, but still should be fine for relatively small graphs; otherwise, it is easy to turn the list into the correct format.

Another variation would be to add more data abstraction: create a class to represent graphs, whose methods implement the various algorithms. While this appeals to the desire for structured programming, it doesn't make the code any more efficient (to the contrary). It does make it easier to add various labels to the nodes or arcs and to add algorithms that take those labels into account (e.g. to find the shortest route between two cities on a map). This, too, will be the subject of another column.

The PSF

The Python Software Foundation is the organization behind Python. Become a member of the PSF and help advance the software and our mission.

• About
  • Applications
  • Quotes
  • Getting Started
  • Help
  • Python Brochure
  • All releases
  • Source code
  • Windows
  • macOS
  • Other Platforms
  • License
  • Alternative Implementations
  • Docs
  • Audio/Visual Talks
  • Beginner's Guide
  • Developer's Guide
  • FAQ
  • Non-English Docs
  • PEP Index
  • Python Books
  • Python Essays
  • Diversity
  • Mailing Lists
  • IRC
  • Forums
  • PSF Annual Impact Report
  • Python Conferences
  • Special Interest Groups
  • Python Logo
  • Python Wiki
  • Code of Conduct
  • Community Awards
  • Get Involved
  • Shared Stories
  • Arts
  • Business
  • Education
  • Engineering
  • Government
  • Scientific
  • Software Development
  • Python News
  • PSF Newsletter
  • PSF News
  • PyCon US News
  • News from the Community
  • Python Events
  • User Group Events
  • Python Events Archive
  • User Group Events Archive
  • Submit an Event
  • Developer's Guide
  • Issue Tracker
  • python-dev list
  • Core Mentorship
  • Report a Security Issue

  Источник

  Python - Graphs

  A graph is a pictorial representation of a set of objects where some pairs of objects are connected by links. The interconnected objects are represented by points termed as vertices, and the links that connect the vertices are called edges. The various terms and functionalities associated with a graph is described in great detail in our tutorial here.

  In this chapter we are going to see how to create a graph and add various data elements to it using a python program. Following are the basic operations we perform on graphs.

  • Display graph vertices
  • Display graph edges
  • Add a vertex
  • Add an edge
  • Creating a graph

  A graph can be easily presented using the python dictionary data types. We represent the vertices as the keys of the dictionary and the connection between the vertices also called edges as the values in the dictionary.

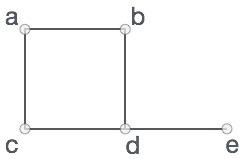
  Take a look at the following graph −

  

  Example

  We can present this graph in a python program as below −

  # Create the dictionary with graph elements graph = < "a" : ["b","c"], "b" : ["a", "d"], "c" : ["a", "d"], "d" : ["e"], "e" : ["d"] ># Print the graph print(graph)

  Output

  When the above code is executed, it produces the following result −

  Display graph vertices

  To display the graph vertices we simple find the keys of the graph dictionary. We use the keys() method.

  class graph: def __init__(self,gdict=None): if gdict is None: gdict = [] self.gdict = gdict # Get the keys of the dictionary def getVertices(self): return list(self.gdict.keys()) # Create the dictionary with graph elements graph_elements = < "a" : ["b","c"], "b" : ["a", "d"], "c" : ["a", "d"], "d" : ["e"], "e" : ["d"] >g = graph(graph_elements) print(g.getVertices())

  Output

  When the above code is executed, it produces the following result −

  Display graph edges

  Finding the graph edges is little tricker than the vertices as we have to find each of the pairs of vertices which have an edge in between them. So we create an empty list of edges then iterate through the edge values associated with each of the vertices. A list is formed containing the distinct group of edges found from the vertices.

  class graph: def __init__(self,gdict=None): if gdict is None: gdict = <> self.gdict = gdict def edges(self): return self.findedges() # Find the distinct list of edges def findedges(self): edgename = [] for vrtx in self.gdict: for nxtvrtx in self.gdict[vrtx]: if not in edgename: edgename.append() return edgename # Create the dictionary with graph elements graph_elements = < "a" : ["b","c"], "b" : ["a", "d"], "c" : ["a", "d"], "d" : ["e"], "e" : ["d"] >g = graph(graph_elements) print(g.edges())

  Output

  When the above code is executed, it produces the following result −

  Adding a vertex

  Adding a vertex is straight forward where we add another additional key to the graph dictionary.

  Example

  class graph: def __init__(self,gdict=None): if gdict is None: gdict = <> self.gdict = gdict def getVertices(self): return list(self.gdict.keys()) # Add the vertex as a key def addVertex(self, vrtx): if vrtx not in self.gdict: self.gdict[vrtx] = [] # Create the dictionary with graph elements graph_elements = < "a" : ["b","c"], "b" : ["a", "d"], "c" : ["a", "d"], "d" : ["e"], "e" : ["d"] >g = graph(graph_elements) g.addVertex("f") print(g.getVertices())

  Output

  When the above code is executed, it produces the following result −

  Adding an edge

  Adding an edge to an existing graph involves treating the new vertex as a tuple and validating if the edge is already present. If not then the edge is added.

  class graph: def __init__(self,gdict=None): if gdict is None: gdict = <> self.gdict = gdict def edges(self): return self.findedges() # Add the new edge def AddEdge(self, edge): edge = set(edge) (vrtx1, vrtx2) = tuple(edge) if vrtx1 in self.gdict: self.gdict[vrtx1].append(vrtx2) else: self.gdict[vrtx1] = [vrtx2] # List the edge names def findedges(self): edgename = [] for vrtx in self.gdict: for nxtvrtx in self.gdict[vrtx]: if not in edgename: edgename.append() return edgename # Create the dictionary with graph elements graph_elements = < "a" : ["b","c"], "b" : ["a", "d"], "c" : ["a", "d"], "d" : ["e"], "e" : ["d"] >g = graph(graph_elements) g.AddEdge() g.AddEdge() print(g.edges())

  Output

  When the above code is executed, it produces the following result −

  Источник