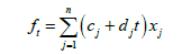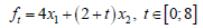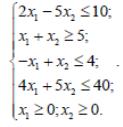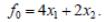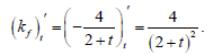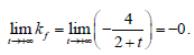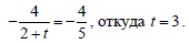Графическое решение задач параметрического программирования

Задачи параметрического программирования

Параметрическое программирование представляет собой один из разделов математического программирования, изучающий задачи, в которых целевая функция или ограничения зависят от одного или нескольких параметров t .

Инструкция . Выберите количество переменных и количество строк (количество ограничений). Полученное решение сохраняется в файле Word . При этом ограничения типа x_i≥0 не учитывайте.

С математической точки зрения параметрическое программирование выступает как одно из средств анализа чувствительности решения к вариации исходных данных, оценки устойчивости решения.

Алгоритм решения задач параметрического линейного программирования

1. Считая значение параметра λ равным некоторому числу λ ₀ ∈ [α, β], находим оптимальный план Х * или устанавливаем неразрешимость полученной задачи линейного программирования.
2. Определяют множество значений параметра λ, для которых найденный оптимальный план является оптимальным или задача неразрешима. Эти значения параметра исключаются из рассмотрения.
3. Полагают значение параметра λ равным некоторому числу, принадлежавшему оставшейся части промежутка [α, β], и находят решение полученной задачи линейного программирования.
4. Определяют множество значений параметра λ, для которых новый оптимальный план остается оптимальным или задача неразрешима. Вычисления повторяются до тех пор, пока не будут исследованы все значения параметра λ ∈ [α, β].

Источник

7. Параметрическое программирование. Постановка и геометрическая интерпретация задачи. Графическое решение задачи.

Задачи параметрического программирования являются обобщением задач линейного программирования. Это обобщение состоит в том, что данные задач параметрического программирования считают не постоянными величинами, а функциями, определенным образом зависящими от некоторых параметров. Целевую функцию задачи оптимального планирования такого производства можно выразить через коэффициенты, линейно зависящие от одного параметра, в частности от времени t. Часто на практике встречаются задачи, в которых значения коэффициентов целевой функции известны лишь приближенно. Представив их в виде линейных функций параметра , можно изучить поведение решений за- дач при различных значениях этих коэффициентов. Аналогично можно провести исследование для случая, когда изменяются коэффициенты сис- темы ограничений t.

8. Параметрическое программирование. Постановка и геометрическая интерпретация задачи. Аналитическое решение задачи.

Этап I. Параметру t дают фиксированное значение, например t =alfa.

Этим задача приводится к задаче линейного программирования. Решая эту задачу симплекс-методом, находят вершину, в которой ft достигает максимума.

Этап II. Определяют интервал изменений параметра t , для которого максимум ft достигается в одной и той же вершине многогранника Omega.

Найденный интервал исключают из отрезка [alfa, beta]. Для оставшейся части отрезка снова решают задачу симплекс-методом, т. е. переходят к этапу I. Решение продолжается до тех пор, пока весь отрезок [alfa, beta] не будет разбит на частичные интервалы.

3. Целочисленное программирование. Метод Гомори решения задач целочисленного программирования.

Под задачей целочисленного программирования понимается задача, в которой все или некоторые переменные должны принимать целые значения. В том случае, когда ограничения и целевая функция представляют собой линейные зависимости, задачу называют целочисленной задачей линейного программирования. В противном случае, когда хотя бы одна зависимость будет нелинейной, это будет целочисленной задачей нелинейного программирования. Если требование целочисленности распространяется на часть неизвестных величин задачи, то такая задача называется частично целочисленной.

Целочисленным (иногда его называют также дискретным) программированием называется раздел математического программирования, изучающий экстремальные задачи, в которых на искомые переменные накладывается условие целочисленности, а область допустимых решений конечна. Огромное количество экономических задач носит целочисленный характер, что связано, как правило, с физической неделимостью многих элементов расчета: например, нельзя построить два с половиной завода, купить полтора автомобиля и т.д.

Для решения целочисленных задач используются следующие методы:

1) симплекс-метод (для транспортных задач, задач о назначениях);

2) метод отсечения (метод Гомори);

3) метод ветвей и границ (в общем случае не обеспечивает получения точного решения);

4) эвристические методы (не обеспечивают получения точного решения).

Метод Гомори основан на применении симплекс-метода и метода отсечения. Сначала находится оптимальное решение задачи целочисленного программирования симплекс-методом. Если полученное решение целочисленное, то цель достигнута. Если же оптимальное решение не является целочисленным, то в условия задачи вводится дополнительное ограничение, которое отсекает от области допустимых решений полученное нецелочисленное решение и не отсекает от нее ни одной точки с целочисленными координатами. Далее симплекс-методом решается расширенная задача, т.е. находится ее опорное и оптимальное решение. Если новое решение не будет целочисленным, то вводится еще одно дополнительное ограничение. Процесс построения дополнительных ограничений и решения задачи симплекс-методом продолжается до тех пор, пока не будет найдено оптимальное целочисленное решение или не будет установлено, что его не существует.

Источник

В6 Параметрическое программирование. Постановка и геометрическая интерпретация задачи. Графическое решение задачи.

Задачи параметрического программирования являются обобщением задач линейного программирования. Это обобщение состоит в том, что данные задач параметрического программирования считают не постоянными величинами, а функциями, определенным образом зависящими от некоторых параметров. Если предположить, например, что произведенная предприятием продукция подлежит хранению, то ее стоимость будет складываться из двух частей: 1) постоянной – стоимости продукции на момент изготовления; 2) переменной, зависящей от срока хранения продукции. Целевую функцию задачи оптимального планирования такого производства можно выразить через коэффициенты, линейно зависящие от одного параметра, в частности от времени .

Часто на практике встречаются задачи, в которых значения коэффициентов целевой функции известны лишь приближенно. Представив их в виде линейных функций параметра , можно изучить поведение решений за- дач при различных значениях этих коэффициентов. Аналогично можно провести исследование для случая, когда изменяются коэффициенты системы ограничений.

В первом выражении числа c_j и d_j известны и постоянны. Остановимся на геометрической интерпретации задачи.

Пусть система ограничений совместна и определяет выпуклый многогранник .

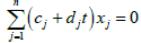
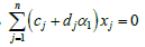
Уравнению соответствует семейство гиперплоскостей, проходящих через начало координат. Если параметру придать некоторое значение t=_0, то гиперплоскость займет вполне определенное положение. Отодвигая ее от начала координат в направлении возрастания функции, получим решение в точке A. Придадим параметру другое значение t=₁ и снова найдем на графике точку оптимума. Гиперплоскость вследствие изменения параметра t повернется вокруг начала координат на некоторый угол. Отодвинув эту гиперплоскость от начала координата, получим оптимальное решение в той же вершине A. Однако значение функции при t 1изменится, так как оно равно взвешенному отклонению точки A от исходной гиперплоскости. При t 2гиперплоскость будет параллельна ребру AB. Оптимальное решение в этом случае будет достигаться в любой точке отрезка AB. Увеличивая t дальше (при t 2), получим оптимальное решение только в вершине B. Для этой вершины будет свой интервал изменения параметра t . Из постановки и геометрической интерпретации задачи следует, что при различных значениях параметра t оптимальный план может оказаться не одним и тем же. Поэтому в задаче параметрического программирования требуется не просто найти оптимальное решение, а разбить отрезок ; на конечное число интервалов, содержащих такие значения t , для которых оптимальное базисное решение задачи достигается в одной и той же вер-

Если многогранник неограничен, то гиперплоскость f t0 при некоторых значениях параметра t может занять такое положение, что

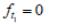
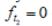
f t max окажется неограниченным. Положение гиперплоскости соответствует неограниченному значению функции, а положение гиперплоскости —

Источник

Графическое решение задачи

Определить интервал изменения параметра t и найти значения переменных x₁ и x₂, при которых максимум линейной функции , достигается в одной и той же вершине области допустимых решений системы ограничений

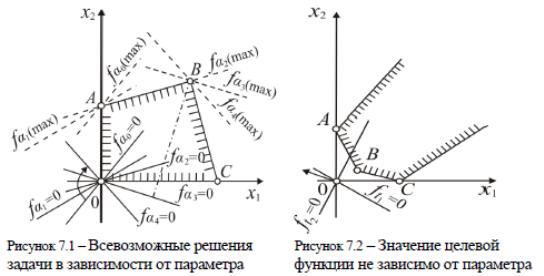
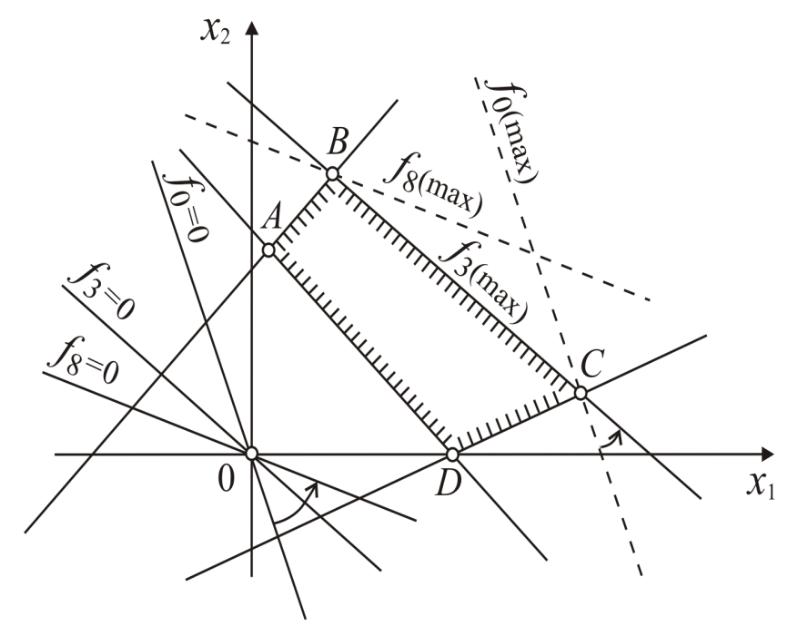
Находим область допустимых решений системы ограничений. Это многоугольник ABCD. Придадим параметру самое малое значение t=0, тогда получим функцию с постоянными коэффициентами

Максимальное значение этой функции достигается в вершине C.

Область допустимых решений задачи

Далее приравняем f_t к нулю и найдем уравнение разрешающей прямой при любом t:

Запишем угловой коэффициент k_f этой прямой и исследуем его поведение при изменении параметра t:

При t=0 его начальное значение k_f = -2

Найдем производную углового коэффициента по параметру t:

Очевидно, что при любом t производная положительна, а угловой коэффициент при увеличении t возрастает. Найдем предел его возрастания:

Так как при t+ угловой коэффициент k_f приближается к нулю со стороны отрицательных значений, то разрешающая прямая поворачивается против часовой стрелки до предельного горизонтального положения. (На- помним, что при вертикальном положении прямой угловой коэффициент как функция терпит разрыв. При вращении прямой против часовой стрелки от оси абсцисс до вертикального положения угловой коэффициент возрастает от 0 до +, при дальнейшем вращении прямой он возрастает от - до 0.)

В рассматриваемом примере при изменении параметра t от нуля до некоторого значения максимум функции будет в вершине C . Далее в некоторый фиксированный момент времени оптимум будет достигаться на отрезке BC , а затем он перейдет в точку B и останется в ней для всех больших значений t .

Определим значение параметра t , при котором решение задачи окажется на отрезке BC . Поскольку в этот момент прямая BC и разрешающая прямая должны быть параллельны, приравняем их угловые коэффициенты. Угловой коэффициент прямой BC kBC 4/5 , следовательно,

Итак, при 0 t 3 оптимальное решение задачи будет в вершине C8,3;1,3, при t 3 оно достигается на всем отрезке BC , а при 3t 8 – в точке B2,2; 6,2.

В7 Параметрическое программирование. Постановка и геометрическая интерпретация задачи. Аналитическое решение задачи.

Алгоритм решения задачи c предыдущего вопроса состоит из двух этапов.

Этап I. Параметру t дают фиксированное значение, например t= . Этим задача приводится к задаче линейного программирования. Решая эту задачу симплекс-методом, находят вершину, в которой f _t достигает максимума.

Этап II. Определяют интервал изменений параметра t , для которого максимум f_t достигается в одной и той же вершине многогранника  . Найденный интервал исключают из отрезка [;]. Для оставшейся части отрезка снова решают задачу симплекс-методом, т. е. переходят к этапу I. Решение продолжается до тех пор, пока весь отрезок [;] не будет разбит на частичные интервалы.

Подробно алгоритм решения рассмотрим на примере.

Пример 1. Найти интервалы изменения параметра t на отрезке [;] для которых достигает максимума в одной и той же вершине области допустимых решений системы ограничений

Источник