Геометрический смысл общей задачи линейного программирования

1.4. Геометрический смысл и графический метод решения задач линейного программирования

Очевидно, множество допустимых решений L задачи ЛП в любой форме записи является выпуклым, как пересечение конечного числа выпуклых множеств. В общем случае оно представляет собой один из следующих объектов:

– многогранник (ограниченный или нет);

Целевую функцию задачи ЛП Z можно геометрически интерпретировать как уравнение гиперплоскости в n-мерном пространстве. Придавая Z различные частные значения, мы будем получать различные гиперплоскости или плоскости уровня целевой функции.

В соответствии с теоремой 4 экстремум Z достигается в крайней точке области L, исходя из этого, предлагается следующий графический метод решения задачи ЛП:

Берем произвольную плоскость (в двумерном пространстве – линию) уровня целевой функции Z (как правило, это плоскость Z = 0, или плоскость нулевого уровня). Пользуясь известным свойством градиента функции нескольких переменных, который направлен в сторону возрастания соответствующей функции, будем перемещать плоскость уровня параллельно самой себе в направлении градиента, пока она не достигнет какой-либо крайней точки области L. Очевидно, мы получим точку максимума Z. Наоборот, перемещая плоскость нулевого уровня в направлении антиградиента Z, в соответствующей крайней точке получим минимум Z. Напомним, что в случае линейной целевой функции

.

Кроме того, градиент всегда перпендикулярен линии уровня целевой функции в той точке, в которой он построен. На практике, применяя графический метод, мы можем наблюдать следующие случаи.

Область ограничена, существуют оба экстремума.

бласть ограничена, минимум достигается в двух крайних точках А и В, следовательно, и на всем отрезке АВ: , 0    1 (рис.1.4.2).

Если L не ограничена, то один из экстремумов Z может не достигаться, однако наличие условий неотрицательности на переменные гарантирует наличие второго экстремума (см. рис.1.4.3):

уществует еще специальный случай:

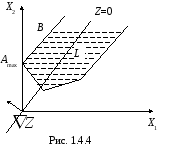
П редельное положение разрешающей гиперплоскости совпадает с бесконечным ребром неограниченной области L (рис. 1.4.4). Известна одна крайняя точка А. В этом случае аналитически находят координаты какой-нибудь другой точки В, лежащей на этом же ребре, и записывают решение задачи в виде:

, 0   < . (1.4.1)

Существенным недостатком графического метода является его ограниченная применимость. Он удобен при размерности n = 2 (иногда n = 3), а при большей размерности его можно использовать только в единственном случае:

Пусть задача содержит только ограничения-равенства в количестве m, причем разность n – m (количество степеней свободы задачи) не больше трех. В этом случае из матрицы А системы ограничений методом Жордана – Гаусса выделяются m базисных переменных, которые выражаются через n – m свободных. Затем применяются ограничения x_j  0, j = 1, 2, …, n, которые дают возможность построить область допустимых решений для свободных переменных в пространстве размерности не более 3. В целевой функции все базисные переменные также выражаются через свободные и находится оптимальное решение графическим методом в пространстве n – m измерений. Затем координаты оптимальной точки подставляются в выражения для базисных переменных и получают решение полной n-мерной задачи.

Пример 1.4.1. Решить графическим методом следующую задачу линейного программирования:

(1.4.2)

Решение. Выпишем матрицу системы ограничений и преобразуем ее методом полного исключения (выделены ведущие элементы):

Источник

Геометрический смысл задачи линейного программирования

В случае двух переменных модель задачи линейного программирования имеет следующий вид:

Каждое ограничение представляет собой прямую, которая разбивает всё пространство (исходную плоскость) на две полуплоскости, одна из которых удовлетворяет ограничению (рис. 1.1).

Система ограничений представляет выпуклое множество, а в рассматриваемом двухмерном случае — выпуклый многоугольник ограничений (рис.1.2).

В частных случаях многоугольник может обращаться в точку (тогда решение единственно), прямую или отрезок. Если система ограничений противоречива (несовместна), то многоугольник ограничений построить нельзя и задача линейного программирования не имеет решений (рис.1.3).

Многоугольник ограничений может быть не замкнут (рис.1.4). В этом случае целевая функция не ограничена.

В случае n переменных каждое ограничение представляет (n-1)-мерную гиперплоскость, которая делит все пространство на два полупространства. Система ограничений в этом случае дает выпуклый многогранник решений — общую часть n-мерного пространства, удовлетворяющую всем ограничениям.

Рис.1.1. Геометрический смысл ограничения

Рис.1.2. Геометрическая интерпретация системы ограничений

Для выяснения геометрического смысла целевой функции придадим переменной Z, различные числовые значения (Z=0, Z=1, Z=2. Z=D).Этим числовым значениям Z соответствует последовательность уравнений и система параллельных прямых в пространстве (рис.1.5).

Рис.1.3. Несовместность системы ограничений

Рис.1.4. Неограниченность целевой функции

Первая прямая (Z=0) проходит через начало координат перпендикулярно (ортогонально) направляющему вектору С=(c₁c₂), последующие прямые параллельны первой и отстоят от нее в направлении вектора С на величину 1, 2. D. В целом переменная Z определяет отклонение точек, лежащих на прямой Z=c₁x₁+c₂x₂ от прямой c₁x₁+c₂x₂=0, проходящей через начало координат. Для того чтобы определить отклонение любой точки от прямой Z=0, достаточно подставить координаты этой точки в уравнение целевой функции.

В n-мерном пространстве целевой функции, приравненной к нулю (Z= c₁x₁+c₂x₂+…+c_jx_j+…+c_nx_n=0), геометрически соответствует (n-1)-мерная гиперплоскость, проходящая через начало координат. Так как линейная форма Z достигает своего экстремального значения в крайней точке (вершине) многогранника ограничений, то геометрически задача линейного программирования заключается в отыскании вершины многогранника допустимых решений, имеющей максимальное уклонение от гиперплоскости, выраженной целевой функцией, приравненной к нулю (рис.1.6).

Рис.1.5.Геометрическая интерпретация целевой функции

Если многогранник ограничений не замкнут (рис.1.4), то уклонение равно бесконечности, так как прямую, параллельную целевой функции, можно перемещать сколько угодно вверх, не выходя за область допустимых значений переменных.

На геометрической интерпретации линейных задач основан графический метод их решения. Этот метод можно эффективно использовать при решении задач с двумя (иногда с тремя) переменными.

Для графического решения задачи линейного программирования необходимо:

1. в принятой системе координат построить уравнения всех ограничений, совокупность которых даст многогранник ограничений;

2. построить уравнение целевой функции, проходящее через начало координат;

3. определить направление роста (убывания) целевой функции, перемещая прямую (плоскость), соответствующую целевой функции, параллельно самой себе или определить градиент целевой функции;

4. в соответствие с целью ЗЛП и направлением роста целевой функции, найти точку касания этой прямой (плоскости) с многоугольником (многогранником) ограничений — вершину многоугольника, имеющую максимальное отклонение от прямой (плоскости), проходящей через начало координат.

Рис.1.6. Геометрический смысл оптимального решения задачи линейного программирования

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник

18.Геометрический смысл задачи линейного программирования

1)Множество всех планов задачи линейного программирования выпукло.

2) Линейная функция задачи линейного программирования достигает своего минимального значения в угловой точке многогранника рещений. Если линейная функция принимает минимальное значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.

20. Доказать, что множество допустимых решений злп является выпуклым множеством

Необходимо доказать, что если Х₁ и Х₂ — планы задачи линейного программирования, то их выпуклая линейная комбинация Х=₁Х₁+₂Х₂, ₁  0, ₂  0, ₁+₂=1 также план задачи.

Так как Х₁ и Х₂ — планы задачи, то выполняются соотношения

получаем, что Х удовлетворяет системе:

x_i  0 (i=1,2. n) (2.53)

Но так как Х₁  0; Х₂  0, ₁  0, ₂  0, то и Х  0, т. е. удовлетворяет и условию (2.53). Таким образом Х — план задачи линейного программирования.

21. Доказать, что оптимум целевой функции злп, если он существует, достигается хотя бы в одной из вершин допустимого множества

Предположим, что многогранник решений ограниченный, имеющий конечное число угловых точек. Обозначим его через К. В двумерном пространстве К имеет вид многоугольника, изображенного на рис. 2.5. Обозначим угловые точки К через Х₁, Х₂, . , Х_p, а оптимальный план — через Х₀. Тогда Z(X₀) Z(X) для всех Х из К. Если Х₀ — угловая точка, то первая часть теоремы доказана. Предположим, что Х₀ не является угловой точкой; тогда Х₀ на основании теоремы 1 можно представить как выпуклую линейную комбинацию угловых точек К, т. е.

Так как Z(X) — линейная функция, получаем

В этом разложении среди значений Z(X_i) (i=1,2. p) выберем наименьшее пусть оно соответствует угловой точке Х_k (1 k  p) и обозначим его через m, т. е. Z(X_k)=m. Заменим в (2.54) каждое значение Z(X_i) этим наименьшим значением. Тогда, так как _i  0 , , то

Z(X₀)  ₁m + ₂m + . +_pm = m .

По предположению, Х₀ — оптимальный план, поэтому, с одной стороны, Z(X₀)  m, но с другой стороны, доказано, что Z(X₀)  m, значит, Z(X₀)=m=Z(X_k), где X_k — угловая точка. Итак, существует угловая точка X_k, в которой линейная функция принимает минимальное значение.

Для доказательства второй части теоремы допустим, что Z(X) принимает минимальное значение более чем в одной угловой точке, например в точках Х₁, Х₂, . , Х_q , 1< q  p; тогда Z(X₁)=Z(X₂)= . =Z(X_q)= m. Если Х — выпуклая линейная комбинация этих угловых точек:

то Z(X)=Z(₁Х₁+₂Х₂+ . +_qХ_q) = ₁Z(X₁) + ₂Z(X₂) + . +_qZ(X_q)=₁m + ₂m + . +_qm = m .

т.е. линейная функция Z принимает минимальное значение в произвольной точке Х, являющейся выпуклой линейной комбинацией угловых точек Х₁, Х₂, . , Х_q .

Источник