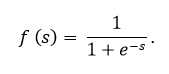Функция активации сигмоида python

Знакомство с простейшей нейронной сетью и ее пошаговая реализация

Однажды я наткнулся на книгу под названием «Создай свою нейросеть», под авторством Тарика Рашида. В отличие от многих других книг по нейронным сетям, в этой все подавалось простым языком, c достаточным количеством примеров и советов

Вдохновившись этой книгой, я хочу пройтись по ней пошагово- а именно по практической ее части — написанию кода простейшей нейронной сети.
Эта статья для тех, кто хочет заниматься нейронными сетями и машинным обучением, но пока с трудом понимает эту удивительную область науки. Ниже будет описан самый простой скелет кода нейронной сети, чтобы многие поняли простейший принцип построения и взаимодействия всего того, из чего состоит эта нейронная сеть.

Теории по машинному обучению и нейронным сетям на хабре и так достаточно. Но если кому-то это необходимо, некоторые ссылки я оставлю в конце статьи. А сейчас, приступаем непосредственно к написанию кода, причем писать мы будем на Python, при написании кода рекомендую использовать Jupyter-Notebook

Шаг 1. Инициализация сети

Сначала нам, конечно же, надо инициализировать все действующие компоненты нашей сети

#импортируем numpy — это библиотека языка Python, добавляющая поддержку больших многомерных массивов и матриц import numpy # импортируем scipy.special , -scipy содержит модули для оптимизации, интегрирования, специальных функций, обработки изображений и многих других задач, нам же здесь нужна наша функция активации, имя которой - "сигмоида " import scipy.special #Вероятно, нам понадобится визуализировать наши данные import matplotlib.pyplot # Определяем класс нейронной сети class neuralNetwork: # Инициализация нашей нейронной сети def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate): #В параметрах мы записываем входные данные, данные скрытого слоя, выходные данные ,скорость обучения соответственно) # устанавливаем количество узлов входного , скрытого слоя, выходного слоя self.inodes = inputnodes self.hnodes = hiddennodes self.onodes = outputnodes # Тут обозначены веса матрицы, wih - вес между входным и скрытым слоем , а так же who- вес между скрытым и выходным слоем self.wih = numpy.random.rand(self.hnodes, self.inodes) self.who = numpy.random.rand(self.onodes, self.hnodes) # Скорость обучения -это наш гиперпараметр, то есть, параметр , который мы подбираем ручками, и в зависимости от того, как нам это удобно нам, и , конечно же, нейронной сети self.lr = learningrate # Наша Сигмоида- функция активации self.activation_function = lambda x: scipy.special.expit(x)

Сигмоида

Эта функция относится к классу непрерывных функций, принимает на вход произвольное вещественное(т.е не обязательно целое) число и на выходе дает вещественное число в интервале от 0 до 1.

В частности, большие (по модулю) отрицательные числа превращаются в ноль, а большие положительные – в единицу.

Выход ее хорошо интерпретируется, как уровень активации нейрона: от отсутствия активации (0) до полностью насыщенной активации (1).

Сигмоида выражается формулой:

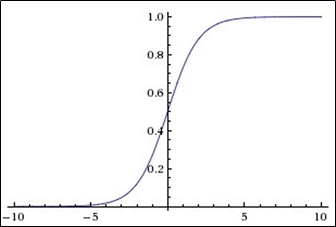
График сигмоидальной функции в соответствии с рисунком ниже:

Сигмоидальная функция является:

Немного о том, как выглядит узел в нейронной сети

На картинке изображен самый, что ни на есть узел, только представлен он обычно в виде круга, а не прямоугольника. Как мы видим, внутри прямоугольника(ну или круга) — это все абстрактно, находятся 2 функции:

1-я Функция занимается тем, что получает все входные, с учетом весов, данные, и иногда даже с учетом нейрона смещения(специальный нейрон, который просто позволяет графикам подвинуться, а не смешиваться в одну некрасивую кучу, вот и все)

2-я Функция принимает в качестве параметра то самое значение, которое суммировала первая функция, и эта вторая функция называется функцией активации. В нашем случае —cигмоида

Часть 2. Тренировка Нейронной Сети

def train(self, inputs_list, targets_list): # Конвертируем наш список в двумерный массив inputs = numpy.array(inputs_list, ndmin=2).T # поступающие на вход данные input targets = numpy.array(targets_list, ndmin=2).T #целевые значения targets # Подсчет сигнала в скрытом слое hidden_inputs = numpy.dot(self.wih, inputs) # Подсчет сигналов, выходящих из скрытого слоя к выходному слою. Тут в нашем узле, куда поступали все данные в переменную hidden_inputs (1я функция), эта переменная подается как параметр в Сигмоиду - функцию активации (2я функция) hidden_outputs = self.activation_function(hidden_inputs) # Подсчет сигналов в конечном(выходном) слое final_inputs = numpy.dot(self.who, hidden_outputs) # Подсчет сигналов, подающихся в функцию активации final_outputs = self.activation_function(final_inputs) # Значение ошибки (Ожидание - Реальность) output_errors = targets - final_outputs # Ошибка скрытого слоя становится ошибкой ,которую мы получили для ошибки выходного слоя, но уже распределенные по весам между скрытым и выходным слоями(иначе говоря с учетом умножения соответствующих весов) hidden_errors = numpy.dot(self.who.T, output_errors) # Обновление весов между скрытым слоем и выходным (Явление того, что люди зовут ошибкой обратного распространения) self.who += self.lr * numpy.dot((output_errors * final_outputs * (1.0 - final_outputs)), numpy.transpose(hidden_outputs)) # Обновление весов между скрытым слоем и входным(Та же ошибка ошибка обратного распространения в действии) self.wih += self.lr * numpy.dot((hidden_errors * hidden_outputs * (1.0 - hidden_outputs)), numpy.transpose(inputs)) 

И вот мы приближаемся к концу

Часть 3. Опрос нейронной сети

#Создаем функцию , которая будет принимать входные данные def query(self, inputs_list): # Конвертируем поданный список входных данных в двумерный массив inputs = numpy.array(inputs_list, ndmin=2).T # Подсчет сигналов в скрытом слое hidden_inputs = numpy.dot(self.wih, inputs) # Подсчет сигналов, поданных в функцию активации hidden_outputs = self.activation_function(hidden_inputs) #Подсчет сигналов в конечном выходном слое final_inputs = numpy.dot(self.who, hidden_outputs) #Подсчет сигналов в конечном выходном слое, переданных в функцию активации final_outputs = self.activation_function(final_inputs) return final_outputs

Доводим дело до конца

 #Подаем конкретное значение для входного , скрытого ,выходного слоев соответственно(указываем количество нод- узлов в ряду входного, скрытого, выходного соответственно input_nodes = 3 hidden_nodes = 3 output_nodes = 3 # Возьмем коэффициент обучения - скорость обучения равной, например. 0.3! learning_rate = 0.3 # Создаем нейронную сеть(n это объект класса neuralNetwork , при его создании запустится конструктор __init__ , и дальше все будет включаться по цепочке n = neuralNetwork(input_nodes,hidden_nodes,output_nodes, learning_rate)

P.S

Выше была представлена способная на вычисления, простейшая модель нейронной сети. Но какого-то конкретного применения показано не было.

При желании, можно пойти дальше, добавив возможность распознавания рукописного текста в код MNIST, для этого вы можете полностью разобраться(и просто позабавиться), имея этот jupyter-файл , моя же задача была продемонстрировать код и по возможности разжевать что в сети присутствует и за что отвечает

P.P.S

Ниже вы найдете полезные ссылки:

1.Cсылка на Github Тарика ->
2.Его книга ->
3.Теория по машинному обучению ->
4.Теория по машинному обучению ->
5.Теория по машинному обучению ->

Источник

The sigmoid activation function in Python

If you’re learning about neural networks, chances are high that you have come across the term activation function. In neural networks, an activation function decides whether a particular neuron will be activated or not. Activation functions take the weighted summation of the nodes as input and perform some mathematical computation, depending on the activation function, and output a value that decides whether a neuron will be activated or not.

They are many activation functions like

In this tutorial, we will be learning about the sigmoid activation function. So let’s begin!

What is the sigmoid function – The math behind it

Sigmoid is a non-linear activation function. It is mostly used in models where we need to predict the probability of something. As probability exists in the value range of 0 to 1, hence the range of sigmoid is also from 0 to 1, both inclusive.
Let’s have a look at the equation of the sigmoid function.

Sigmoid is usually denoted using the Greek symbol sigma. So, we can also write

In the above equation, ‘e‘ is Euler’s number. Its value is approximately 2.718. Similarly,

In fact, we can derive a relation between the above two equations as

We can also prove this relation as shown below:

It can also be written as

Hence, we have proved the relation.

Another property of the sigmoid activation function is that it is differentiable. Let us see how we can differentiate it.

Differentiating sigmoid equation 1 we get

So, from Sigmoid Equation 1, Sigmoid x And -x Relation Equation 2 and Sigmoid Differentiation Equation 2, we can write

Phew! That’s a lot of maths! Now, let us have a look at the graph of the sigmoid function.

Sigmoid graph using Python Matplotlib

#importing the required libraries from math import exp from matplotlib import pyplot as plt #defining the sigmoid function def sigmoid(x): return 1/(1+exp(-x)) #input input = [] for x in range(-5, 5): input.append(x) #output output = [] for ip in input: output.append(sigmoid(ip)) #plotting the graph plt.plot(input, output) plt.title("Sigmoid activation function") plt.grid() #adding labels to the axes plt.xlabel("x") plt.ylabel("sigmoid(x)") plt.scatter([0], [0.5], color="red", zorder=5) plt.show()

The above plot leads us to a few properties of the sigmoid function. They are:

• S-shaped: The graph of sigmoid is S-shaped just like the graph of tanh activation function.
• Domain: The domain of sigmoid is (-∞, +∞).
• Continuous: The sigmoid function is continuous everywhere.
• The sigmoid function is monotonically increasing.
• sigmoid(0)= 0.5

Relation between sigmoid and tanh

We have previously discussed the tanh activation function in our tutorial.

These two functions are related:

Summary

Let’s have a quick recap: The sigmoid activation function is non-linear, monotonic, S-shaped, differentiable, and continuous. That’s all! We have learned about the sigmoid activation function and also its properties.

Hope you found this tutorial helpful. Do check out more such tutorials related to Python here.

Источник