Finite difference method python

Solve Non-Linear Differential Equations numerically using the Finite Difference Method

In this article we will see how to use the finite difference method to solve non-linear differential equations numerically. We will practice on the pendulum equation, taking air resistance into account, and solve it in Python.

We will find the differential equation of the pendulum starting from scratch, and then solve it. Before we start, we need a little background on Polar coordinates.

Polar Coordinates

You already know the famous Cartesian coordinates, which are probably the most used in everyday life. However, in some cases, describing the position of an object in Cartesian coordinates isn’t practical. For instance, when an object is in a circular movement, sine and cosine functions are going to pop all over the place, so it’s generally a much better idea to describe that object’s position in what we call Polar coordinates.

Polar coordinates are described by two variables, the radius ρ and the angle θ. We attach unit vectors to each variable:

• eρis a unit vector always pointing in the same direction as vector OM.
• eθis a unit vector perpendicular to eρ.

Our goal now is to express the position, velocity, and acceleration of an object in Polar coordinates. For this we need to express the relationship between the Polar unit vectors and the Cartesian unit vectors.

All right! Let’s express position, velocity, and acceleration in Polar coordinates.

Position

This one is quite easy. It’s the whole point of using Polar coordinates!

Velocity

We simply differentiate the position with respect to time. We will assume ρ is a constant, and only θ varies over time.

Acceleration

We differentiate the velocity with respect to time.

All right! We can now work on our problem: the pendulum.

Pendulum Equation

In order to find the equation that the angle θ satisfies, we will use Newton’s second law of motion, or as we call it in French, the fundamental principle of dynamic.

The sum of all the forces applied to a system is equal to its mass times its acceleration. Let’s enumerate all the forces applied to the pendulum and express them in Polar coordinates.

Weight

The weight of the object due to gravity is one the forces applied to the object. Its formula is well known, and will be expressed in our coordinate system as:

Where m (kg) is the mass of the object, and g (m/s²) is value of the acceleration of gravity — which is about 9.81 on earth.

Rope Tension

The rope exerts a tension pulling the pendulum in the direction of the rope.

Where R (N) is the rope tension in Newtons.

Air Resistance

Of course, the air exerts a friction on the pendulum, which will make it stop oscillating at some point. Small air resistance is usually modeled as a force opposite to the velocity vector and proportional to the norm of the velocity vector.

Where k (kg/s) is the friction coefficient that is specific to the object in movement, and L (m) is the length of the pendulum rope.

Newton’s second law of motion

We can now apply Newton’s second law of motion:

Then project the result on both axes:

Reordering the terms of the second equation, we get:

Solving this second order non-linear differential equation is very complicated. This is where the Finite Difference Method comes very handy. It will boil down to two lines of Python! Let’s see how.

Finite Difference Method

The method consists of approximating derivatives numerically using a rate of change with a very small step size.

That is the very definition of what a derivative is. Numerically, if we knew f, we could take a small number h — e.g. 0.0001 — and compute the above formula for a given x, which would give us an approximation of f’(x).

The finite difference method simply uses that fact to transform differential equations into ordinary equations.

In our case, we start by expressing θ’’ with respect to θ’ using the rate of change.

I removed the limit, and wrote dt for us to know that this is supposed to be an infinitesimal value — in practice, just a very small number. We will now plug this equation into the pendulum equation.

Okay! We managed to express the angular velocity at time t+dt with respect to the angle and angular velocity at time t. In other words, if for instance dt=0.001 and if you know θ(0) and θ’(0) (which are the initial conditions of the system), then you can compute θ’(0.001)! If we could also compute θ(0.001) then the recursion is complete and we can compute [θ(t), θ’(t)] for any t starting with known initial conditions.

Fortunately, there is a way to compute θ(t+dt):

All right! With that equation in hand we can also compute the angle at time t+dt given the angle and the angular velocity at time t.

Using these two equations we can now compute the angle theta at any time step!

Indeed, given [θ(0), θ’(0)] you can compute [θ(dt), θ’(dt)]. Given [θ(dt), θ’(dt)] you can compute [θ(2dt), θ’(2dt)], and so on.

Let’s put all this to use in a Python program!

Python Code

• The angular velocity seems to reach extremums when the angle is zero, which makes sens since this is where the pendulum has accumulated all its inertia and is about to slow down because it’s going up.
• The angular velocity seems to reach zero when the angle reaches an extremum, which makes sens since this is when the pendulum is slowing down and is about to go in the other direction.

Playing with the code a little, you might want to set the initial velocity to 2π for instance.

Notice how the angle keep increasing before going down. What happened is that the initial velocity was high enough to make the pendulum make a full spin before entering the usual oscillation!

One last thing… You can try to increase dt and see how this affects the simulation. Hopefully you’ve understood that a smaller dt means more accurate results. Let’s see what happens for N=3,2,1.

I was actually surprised to see that for only 3 points per second (and even 2), we still manage to get the general shape of the solution. N=1 is another story…

Conclusion

In this article we have seen how to use the finite difference method to solve differential equations (even non-linear) and we applied it to a practical example: the pendulum. This technique also works for partial differential equations, a well known case is the heat equation.

Источник

Finite Difference Method

This document uses the open source Jupyter Notebook and the Python programming language to demonstrate a finite difference numerical method for solving a differential equation.

%matplotlib inline # Required libraries import numpy as np import matplotlib.pyplot as plt import seaborn as sns # Seaborn aesthetics sns.set_context("paper", font_scale=1.8, rc=) sns.set_style("ticks") 

Beam Deflection Problem

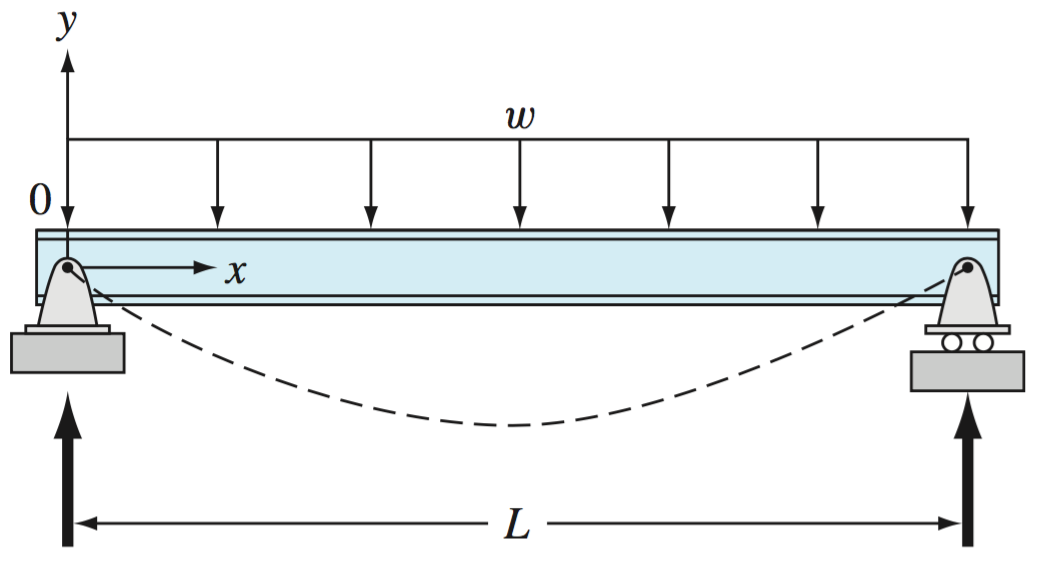
Figure 1. Uniformly-loaded beam (Chapra, p. 639).

The basic differential equation of the elastic curve for a simply supported, uniformly loaded beam (Fig. 1) is given as

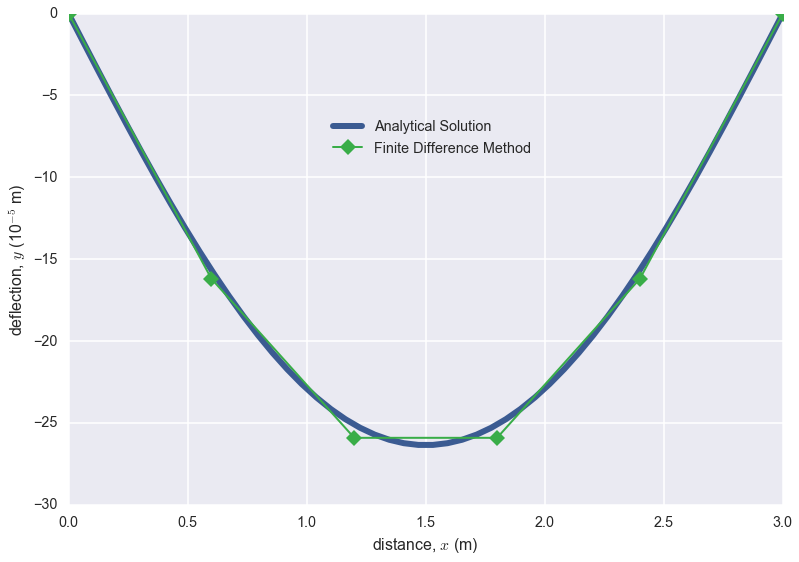
where $E=$ the modulus of elasticity, and $I=$ the moment of inertia. The boundary conditions are $y(0)=y(L)=0$. Solve for the deflection of the beam using the finite-difference approach $(\Delta x = 0.6 m)$. The following parameter values apply: $E = 200$ GPa, $I = 30,000$ cm$^4$, $w = 15$ kN/m, and $L = 3$ m. Compare your numerical results to the analytical solution:

Analytical Solution

def y(x): """ Vertical deflection, y, of the beam in 10E-5 m. """ E = 200 _ 10**9 # Pa I = 30000 / 100**4 # m^4 w = 15 _ 1000 # N/m L = 3 # m return ((w*L*x**3)/(12*E*I) - (w\*x**4)/(24*E*I) - \ (w*x*L**3)/(24*E*I)) \* 10**5 

Central Difference Method

def cdiff_beam(L,ya,yb,n): """ Approximate vertical deflection, y, of the beam in 10E-5 m, using central difference method. Args: L = length of the beam, m ya = vertical deflection at x = 0 yb = vertical deflection at x = L n = desired number of interior segments """ E = 200 _ 10**9 # Pa I = 30000 / 100**4 # m^4 w = 15 _ 1000 # N/m i = 0 x = 0 dx = L/n X = [x] A = np.zeros(shape=(n+1,n+1)) b = np.zeros(shape=(n+1,1)) while i < n-1: i = i + 1 x = x + dx b[i] = dx**2 * (1/(2*E*I)) * (w*L*x - w\*x**2) A[i][i] = -2 if i < n: A[i][i+1] = 1 A[i][i-1] = 1 X = np.append(X, x) A[0][0] = 1 A[n][n] = 1 b[0] = ya b[n] = yb X = np.append(X, x+dx) Y = np.linalg.solve(A,b) # print(A); print(b) return X, Y 

Plot of Solutions

x = np.linspace(0,3) X,Y = cdiff_beam(3,0,0,8) plt.plot(x,y(x), lw=7, alpha=0.6, label="Analytical Solution") plt.plot(X,Y*10**5, "o-", lw=2, ms=8, color="#c44e52", label="Finite Difference Method") plt.legend(bbox_to_anchor=[0.665, 0.81]) plt.xlabel("distance, $x$ (m)") plt.ylabel("deflection, $y$ (10$^$ m)") sns.despine() plt.show() 

Loaded Beam

Источник

Saved searches

Use saved searches to filter your results more quickly

You signed in with another tab or window. Reload to refresh your session. You signed out in another tab or window. Reload to refresh your session. You switched accounts on another tab or window. Reload to refresh your session.

Finite-difference methods for solving initial and boundary value problems of some linear partial differential equations.

License

olivertso/pdepy

This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.

Name already in use

A tag already exists with the provided branch name. Many Git commands accept both tag and branch names, so creating this branch may cause unexpected behavior. Are you sure you want to create this branch?

Sign In Required

Please sign in to use Codespaces.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching Xcode

If nothing happens, download Xcode and try again.

Launching Visual Studio Code

Your codespace will open once ready.

There was a problem preparing your codespace, please try again.

Latest commit

Git stats

Files

Failed to load latest commit information.

README.md

A Python 3 library for solving initial and boundary value problems of some linear partial differential equations using finite-difference methods.

• Laplace
  • Implicit Central
  • Explicit Central
  • Explicit Upwind
  • Implicit Central
  • Implicit Upwind
  • Explicit
  • Implicit

  import numpy as np from pdepy import laplace xn, xf, yn, yf = 30, 3.0, 40, 4.0 x = np.linspace(0, xf, xn + 1) y = np.linspace(0, yf, yn + 1) f = lambda x, y: (x - 1) ** 2 - (y - 2) ** 2 bound_x0 = f(0, y) bound_xf = f(xf, y) bound_y0 = f(x, 0) bound_yf = f(x, yf) axis = x, y conds = bound_x0, bound_xf, bound_y0, bound_yf laplace.solve(axis, conds, method="ic")

  import numpy as np from pdepy import parabolic xn, xf, yn, yf = 40, 4.0, 50, 0.5 x = np.linspace(0, xf, xn + 1) y = np.linspace(0, yf, yn + 1) init = x ** 2 - 4 * x + 5 bound = 5 * np.exp(-y) p, q, r, s = 1, 1, -3, 3 axis = x, y conds = init, bound, bound params = p, q, r, s parabolic.solve(axis, params, conds, method="iu")

  import numpy as np from pdepy import wave xn, xf, yn, yf = 40, 1.0, 40, 1.0 x = np.linspace(0, xf, xn + 1) y = np.linspace(0, yf, yn + 1) d_init = 1 init = x * (1 - x) bound = y * (1 - y) axis = x, y conds = d_init, init, bound, bound wave.solve(axis, conds, method="i")

  Create virtual environment and install requirements:

  Run command in virtual environment:

  Источник