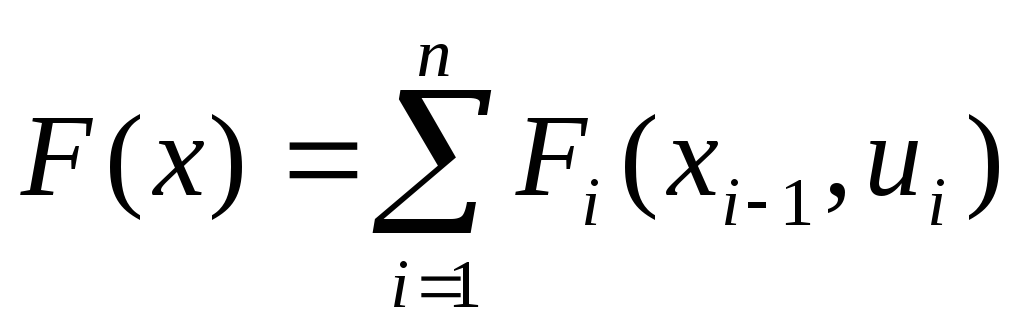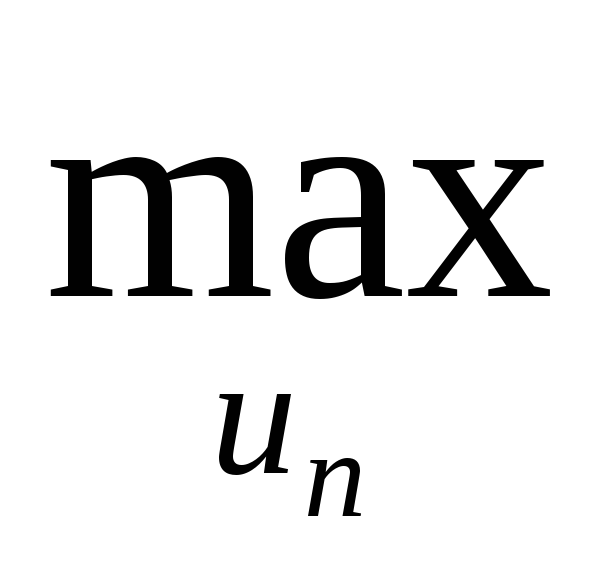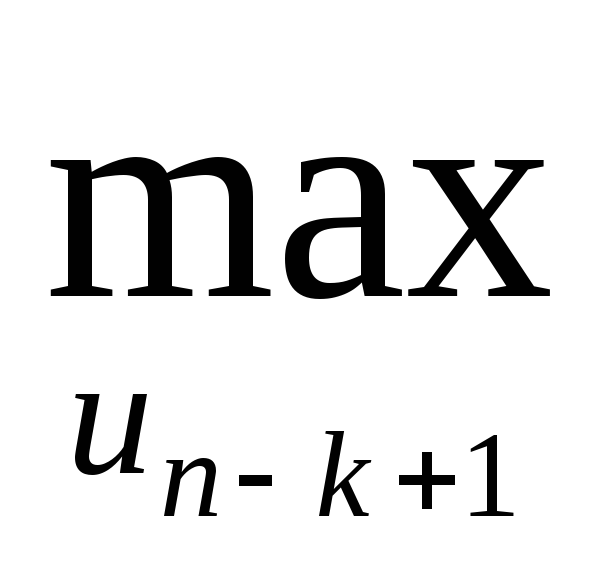Динамическое программирование в экономическом анализе
При решении задач линейного и нелинейного программирования, экономические процессы считаются статическими, т.е. не зависят от времени, в связи с чем оптимальное решение находилось на один этап. Такие задачи называются одноэтапными или одношаговыми.
Экономический процесс в задачах динамического программирования зависит от времени, т.е. от нескольких временных периодов, поэтому определяются оптимальные решения для каждого этапа, обеспечивающие оптимальное развитие целого процесса. Динамическое программирование является многоэтапным (многошаговым).
Динамическое программирование – это математический аппарат, который позволяет проводить оптимальное планирование многоэтапных управляемых процессов, а также процессов, которые зависят от времени. Управляемым экономический процесс становится тогда, когда можно воздействовать на его развитие. Управление – это совокупность решений, которые принимаются на каждой стадии влияния на процесс. Управление в экономических процессах состоит в распределении и перераспределении ресурсов на всех этапах.
К примеру, выпуск товаров предприятием – это управляемый процесс, поскольку он определен изменением количества оборудования, объемами финансирования, поставками сырья и т.д. Все решения, принимаемые в начале каждого периода по обеспечению организации ресурсами, сырьем, оборудованием, по размерам финансирования, а также по замене оборудования, являются управлением. На первый взгляд может показаться, что для получения максимальных объемов выпуска продукции, самым простым вариантом будет вложение максимально возможного количества средств и использование оборудования на полную мощность. Однако, это приведет к быстрому износу оборудования, а, следовательно, к снижению выпуска продукции. Таким образом, выпуск продукции необходимо спланировать так, чтобы оградиться от нежелательных эффектов. Стоит предусматривать мероприятия по пополнению оборудования по мере его изнашивания. Это хотя и снижает первоначальные объемы выпускаемой продукции, но в дальнейшем обеспечивает возможность наращивания производства. Так, экономический процесс состоит из нескольких этапов, действие каждого влияет на общее развитие. Управляемый процесс начинается, когда принимается какое-либо решение о замене оборудования, объемах капитальных вложений и т.д. Планирование многоэтапного процесса подразумевает учет интересов всего процесса, другими словами, при принятии любого решения всегда следует учитывать конечную цель.
С помощью динамического программирования можно упростить решение задач, а также решить такие, в которым нет возможности применить приемы и способы математического анализа. Упростить решение можно посредством уменьшения количества изучаемых вариантов, поскольку для решения сложной многовариантной задачи в методе поэтапного планирования предполагается многократное решение простых задач.
Между тем, в динамическом программировании есть и недостатки. Например, в линейном программировании является универсальным симплексный метод, а в динамическом такого метода нет. Также недостатком динамического программирования является трудоемкость решения многомерных задач.
Постановка задачи динамического программирования
Рассмотрим постановку задачи динамического программирования на примере инвестирования, которое связано с распределением ресурсов между предприятиями. При управлении инвестициями система постепенно переводится из состояния $S_0$ в состояние $S_n$. Предполагается, что управление можно разделить на шаги, а решение будет приниматься последовательно на каждом этапе. Управление будет представлять собой совокупность n управлений. Каждый шаг содержит две переменных: переменную управления $x_k$ и переменную состояния $S_k$. Переменная $S_k$ показывает, в каком состоянии может находиться система на $k$-м шаге. Состояние $S$ определяет управления, которые описываются переменной $x_k$ и удовлетворяют некоторым ограничениям.
Предположим, что $X=(x_1, x_2, …, x_k,… , x_n)$ – это управление, которое переводит систему из положения $S_0$ в $S_n$, а $S_k$ – это состояние системы на $k$ шаге. Последовательность состояний данной системы в таком случае можно изобразить в виде графа (Рисунок 1).
Рисунок 1. Состояния системы. Автор24 — интернет-биржа студенческих работ
Управляющее воздействие $x_k$ на любом шаге переводит систему в другое состояние, которое приносит результат. Для каждого состояния на всех шагах определяется оптимальное управление $x^*_k$, которое позволяет достичь оптимальный результат. Числовая характеристика такого результата носит название функция Беллмана $F(k)(S)$ и зависит от шага $k$, а также от состояния системы $S$.
Формулировка задачи динамического программирования такова: необходимо выявить такое управление $X^*$, которое переводит систему из состояния $S_0$ в $S_n$, а целевая функция при этом принимает наименьшее (наибольшее) значение $F(S_0, X^*)→extr$.
Характерные черты задачи динамического программирования состоят в следующем:
- Задача оптимизации является конечным многошаговым процессов управления;
- Выигрыш (целевая функция) имеет вид аддитивной и равняется сумме целевых функций на каждом шаге;
- Определение управления на каждом шаге находится в зависимости от состояния систем перед этим шагом и не воздействует на предшествующие шаги (обратной связи нет);
- Состояние системы $S_k$ зависит только от состояния $S_$ и управляющего воздействия $x_k$;
- $X_k$ на любом шаге управления зависит от числа переменных управляющего типа, положение системы $S_k$ находится в зависимости от числа параметров;
- Оптимальным управлением является вектор $X^*$, который определяется последовательностью оптимальных управлений на каждом шаге: $X=(x^*_1, x^*_2, …, x^*_k, …, x^*_n)$, а количество управлений определяет число шагов в задаче.
Лекция 7,8. Метод динамического программирования.
Вопросы: 1. Основные понятия. Общая постановка задачи ДП.
2. Принцип оптимальности. Функциональные уравнения Беллмана.
3. Задача оптимального распределения ресурсов.
5. Задача управления производством и запасами.
1.Основные понятия. Общая постановка задачи динамического программирования.
Динамическое программирование — метод оптимизации, приспособленный к операциям, в которых процесс принятия решений может быть разбит на отдельные этапы, шаги.
Такие операции называются многошаговыми. Многие экономические процессы расчленяются на шаги естественным образом. Это процессы планирования и управления, развиваемые во времени. Естественным шагом может быть год, квартал, месяц и т.д. Т.о., если управление сводится к однократному принятию решения, то соответствующая задача называется одноэтапной или одношаговой. Ранее решаемые задачи линейного и нелинейного программирования – примеры подобных задач.Если управление требует некоторой последовательности принятых решений, то такая задача называется многоэтапной или многошаговой.
Рассмотрим некоторую управляемую систему, характеризующуюся определенным набором параметров, задающих ее состояния. Система под влиянием управления переходит из начального состояния в конечное. Введем обозначения.
1. xi–многомерный вектор, компоненты которого определяют состояние системы на
i-том шаге. Дальнейшее изменение состояния зависит только от данного состояния и не
зависит от того, каким путем система перешла в него (процесс без последствия).
2.На каждом шаге выбирается одно решение,управление ui, под действием которого
система переходит из предыдущего состояния xi-1 в новое xi. Это новое состояние
является функцией состояния на начало шага xi-1и принятого в начале решенияui, т.е.
3. Действие на каждом шаге связано с определенным выигрышем (доходом, прибылью)
или потерей (издержками), которые зависят от состояния на начало шага и принятого
решения. Fi – приращение целевой функции задачи в результате i-того шага,
аналогично, Fi = Fi ( xi-1 , ui ).Тогда значение целевой функции при переходе системы
из начального состояния в конечное за nшагов
.
4.На векторы состояния хiи управленияuiмогут быть наложены ограничения,
объединение которых составляет область допустимых решений uU.
5.Требуется найти такое допустимое управлениеu* = (u1* ,…,un* ) (для каждого шага),
чтобы получить экстремальное значение функции цели F* за всеnшагов.
Любая последовательность действий для каждого шага, переводящая систему из начального состояния в конечное, называется стратегией управления.
Допустимая стратегия управления, доставляющая функции цели экстремальное значение, называется оптимальной.
2. Принцип оптимальности. Функциональные уравнения Беллмана.
Метод динамического программирования состоит в том, что оптимальное управление строится постепенно, шаг за шагом. На каждом шаге оптимизируется управление только этого шага. Вместе с тем на каждом шаге управление выбирается с учетом последствий, т.к. управление, оптимизирующее целевую функцию только для данного шага, может привести к неоптимальному эффекту всего процесса. Управление на каждом шаге должно быть оптимальным с точки зрения процесса в целом. В основе метода динамического программирования лежит принцип оптимальности, сформулированный Беллманом.
Принцип оптимальности: если некоторая последовательность решений оптимальна, то на любом шаге последующие решения образуют оптимальную стратегию по отношению к результату предыдущих решений.
Другими словами, каково бы не было состояние системы перед очередным шагом, надо выбрать управление на этом шаге так, чтобы выигрыш на данном шаге (проигрыш) плюс оптимальный выигрыш (проигрыш) на всех последующих шагах был бы максимальным (минимальным). На основе принципа оптимальности Беллмана строится схема решения монгошаговой задачи, состоящая из 2-х частей:
1) Обратный ход:от последнего шага к первому получают множество возможных оптимальных («условно-оптимальных») управлений.
2) Прямой ход:от известного начального состояния к последнему из полученного множества «условно-оптимальных» управлений составляется искомое оптимальное управление для всего процесса в целом.
Оптимальную стратегию управления можно получить, если сначала найти оптимальную стратегию управления на n-м шаге, затем на двух последних шагах, затем на трех последних шагах и т.д., вплоть до первого шага.
Чтобы можно было использовать принцип оптимальности практически, необходимо записать его математически. Обозначим через z1(xn-1),z2(xn-2),…,zn(x0) условно-оптимальные значения приращений целевой функции на последнем шаге, двух последних,…, на всей последовательности шагов, соответственно.
Тогда для последнего шага:
z1(xn-1) =(min) n(xn-1,un)>,
где un– множество допустимых (возможных) управлений наn-ом шаге,xn-1– возможные состояния системы передn-ым шагом.
Для двух последних шагов:
z2(xn-2) =(min) n-1(xn-2,un-1) +z1(xn-1)>.
Для k последних шагов:
zk(xn-k) = (min) n-k+1(xn-k, un-k+1) + zk-1(xn-k+1)>.
Для всех n шагов:
zn(x0) = (min) 1(x0, u1) + zn-1(x1)>.
Полученные рекуррентные соотношения называют функциональными уравнениями Беллмана.
При этом согласно определению zn(x0) =F*.