The Simple Tutorial to Disjoint Set (Union Find Algorithm)
Disjoint Sets is one of the most powerful and yet simple data structure. The idea of Disjoint Sets can be perfectly applied in finding the minimal spanning tree. The Disjoint Sets consist of two basic operations: finding the group (parent) of any element, unioning two or more sets.
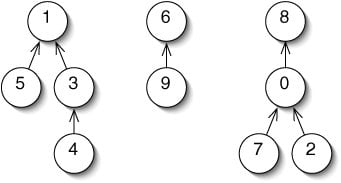
Considering above forests (a set of trees), each tree represents a set. We use an one-dimension array to store the fathers of every node. We can initialize them by -1 or itself, meaning they belong to their own group at the begining. Otherwise, the value represents its father node.
Finding the root-parent of any group can be implemented by two styles: recursive or iterative. The recursive method is short and straightforward.
def find(x): global father if x != father[x]: father[x] = find(x) // compress the paths return father[x]
def find(x): global father if x != father[x]: father[x] = find(x) // compress the paths return father[x]
The iterative approach is more efficient and it avoids stack overflow if the path sometimes is degenerated into a linked-list. In this case, the root-finding complexity will be .
def find(x): global father px = x while px != father[px]: px = father[px] // trace to root // path compression while x != px: i = father[x] father[x] = px // link to root x = i return px
def find(x): global father px = x while px != father[px]: px = father[px] // trace to root // path compression while x != px: i = father[x] father[x] = px // link to root x = i return px
By checking the root-parents of two element, we can judge if they belong to the same set (same tree).
def same(x, y): return find(x) == find(y)
def same(x, y): return find(x) == find(y)
The above shows how to union two sets. We can simply point the father of one element to the other element in other set. e.g. father[x] = y where x and y belong to different sets. The rank array is optional. It represents the depth of an element. We can use the rank to merge two sets i.e. by pointing the less-depth set to a more-depth set.
def union(x, y): global father, rank x = find(x) y = find(y) if x == y: return // same set if rank[x] > rank[y]: father[y] = x else: if rank[x] == rank[y]: rank[y] += 1 // update the rank father[x] = y
def union(x, y): global father, rank x = find(x) y = find(y) if x == y: return // same set if rank[x] > rank[y]: father[y] = x else: if rank[x] == rank[y]: rank[y] += 1 // update the rank father[x] = y
We can keep a shorter (less depth) tree in this method, which will shorten the time in finding the root, apart from the optimisation using path compression described above.
Disjoint Sets uses space.
Number of Connected Groups
We can count the number of connected groups by checking the final group IDs:
def size(parents): for i, v in enumerate(parents): if i == v: ans += 1 return ans
def size(parents): for i, v in enumerate(parents): if i == v: ans += 1 return ans
We can also keep a variable counter for the current connected Groups and update it when we merge two components. This will be O(1) time.
Disjoint Set Python Template Class
Here is a template of Python Disjoint Set: https://github.com/DoctorLai/ACM/blob/master/template/DSU.py
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
class UnionFind: def __init__(self, n: int): self.parent = list(range(n)) self.size = [1] * n self.n = n self.setCount = n def findset(self, x: int) -> int: if self.parent[x] == x: return x self.parent[x] = self.findset(self.parent[x]) return self.parent[x] def unite(self, x: int, y: int) -> bool: x, y = self.findset(x), self.findset(y) if x == y: return False if self.size[x] self.size[y]: x, y = y, x self.parent[y] = x self.size[x] += self.size[y] self.setCount -= 1 return True def connected(self, x: int, y: int) -> bool: x, y = self.findset(x), self.findset(y) return x == y
class UnionFind: def __init__(self, n: int): self.parent = list(range(n)) self.size = [1] * n self.n = n self.setCount = n def findset(self, x: int) -> int: if self.parent[x] == x: return x self.parent[x] = self.findset(self.parent[x]) return self.parent[x] def unite(self, x: int, y: int) -> bool: x, y = self.findset(x), self.findset(y) if x == y: return False if self.size[x] < self.size[y]: x, y = y, x self.parent[y] = x self.size[x] += self.size[y] self.setCount -= 1 return True def connected(self, x: int, y: int) ->bool: x, y = self.findset(x), self.findset(y) return x == y
Related Posts
Simple Robot Simulation Algorithm A Roomba robot is currently sitting in a Cartesian plane at (0, 0). You are…
The Simple Console Rocket Animation in Python I have implemented a C/C++ Rocket that launches a rocket in the console in this…
Algorithm Complexity Algorithm complexity can be represented by Big O notation, for example, the following piece of…
Runlength Compression Algorithm, Demonstration in Python This may be used as an interview question for IT-based jobs. The compression algorithms aim…
A Concise Python Function to Check Subsequence using Iterator Given a list/array/string in Python, find out if it is the subsequence of another. A…
Bogo Sort Algorithm Bogosort is a purely random sorting algorithm. It is inefficient because it is probablistic in…
Algorithm to Find the Longest Alliteration Given a list of lowercase alphabet strings words, return the length of the longest contiguous…
Parentheses Grouping Algorithm Given a string s containing balanced parentheses «(» and «)», split them into the maximum…
Disjoint–Set Data Structure (Union–Find Algorithm)
Explain the working of a disjoint–set data structure and efficiently implement it.
Problem: We have some number of items. We are allowed to merge any two items to consider them equal. At any point, we are allowed to ask whether two items are considered equal or not.
What is a disjoint–set?
A disjoint–set is a data structure that keeps track of a set of elements partitioned into several disjoint (non-overlapping) subsets. In other words, a disjoint set is a group of sets where no item can be in more than one set. It is also called a union–find data structure as it supports union and find operation on subsets. Let’s begin by defining them:
Find: It determines in which subset a particular element is in and returns the representative of that particular set. An item from this set typically acts as a “representative” of the set.
Union: It merges two different subsets into a single subset, and the representative of one set becomes representative of another.
The disjoint–set also supports one other important operation called MakeSet , which creates a set containing only a given element in it.
How does Union–Find work?
We can determine whether two elements are in the same subset by comparing the result of two Find operations. If the two elements are in the same set, they have the same representation; otherwise, they belong to different sets. If the union is called on two elements, merge the two subsets to which the two elements belong.
How to Implement Disjoint Sets?
Disjoint–set forests are data structures where each set is represented by a tree data in which each node holds a reference to its parent and the representative of each set is the root of that set’s tree.
- Find follows parent nodes until it reaches the root.
- Union combines two trees into one by attaching one tree’s root into the root of the other.
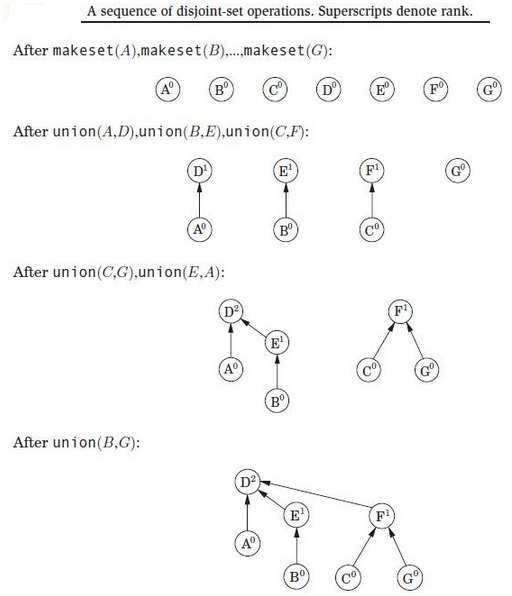
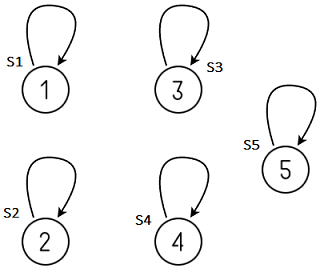
For example, consider five disjoint sets S1 , S2 , S3 , S4 , and S5 represented by a tree, as shown below diagram. Each set initially contains only one element each, so their parent pointer points to itself or NULL .
The Find operation on element i will return representative of S i , where 1 Find(i) = i .
If we do Union (S3, S4) , S3 and S4 will be merged into one disjoint set, S3 . Now,
Find(4) will return representative of set S3 , i.e., Find(4) = 3
If we do Union (S1, S2) , S1 and S2 will be merged into one disjoint set, S1 . Now,
Find(2) or Find(1) will return the representative of set S1 , i.e., Find(2) = Find(1) = 1
If we do Union (S3, S1) , S3 and S1 will be merged into one disjoint set, S3 . Now,
One way of implementing these might be:
function MakeSet(x)
x.parent = x
function Find(x)
if x.parent == x
return x
else
return Find(x.parent)
function Union(x, y)
xRoot = Find(x)
yRoot = Find(y)
xRoot.parent = yRoot
Following is the C++, Java, and Python implementation of union–find that uses a hash table to implement a disjoint set:
C++
Output:
1 2 3 4 5
1 2 3 3 5
1 1 3 3 5
3 3 3 3 5
Java
Output:
1 2 3 4 5
1 2 3 3 5
1 1 3 3 5
3 3 3 3 5
Python
Output:
[1, 2, 3, 4, 5][1, 2, 3, 3, 5]
[1, 1, 3, 3, 5]
[3, 3, 3, 3, 5]
The above approach is no better than the linked list approach because the tree it creates can be highly unbalanced; however, we can enhance it in two ways.
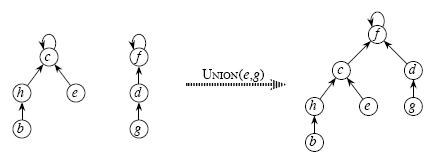
1. The first way, called union by rank , is to always attach the smaller tree to the root of the larger tree. Since it is the depth of the tree that affects the running time, the tree with a smaller depth gets added under the root of the deeper tree, which only increases the depth of the depths were equal. Single element trees are defined to have a rank of zero, and whenever two trees of the same rank r are united, the result has the rank of r+1 . The worst-case running-time improves to O(log(n)) for the Union or Find operation.
2. The second improvement, called path compression , is a way of flattening the tree’s structure whenever Find is used on it. The idea is that each node visited heading to a root node may as well be attached directly to the root node; they all share the same representative. To effect this, as Find recursively traverses up the tree, it changes each node’s parent reference to point to the root that is found. The resulting tree is much flatter, speeding up future operations not only on these elements but on those referencing them, directly or indirectly.
Pseudocode for the improved MakeSet and Union :
function MakeSet(x)
x.parent = x
x.rank = 0
function Union(x, y)
xRoot = Find(x)
yRoot = Find(y)
if xRoot == yRoot
return
// x and y are not already in the same set. Merge them.
if xRoot.rank < yRoot.rank
xRoot.parent = yRoot
else if xRoot.rank > yRoot.rank
yRoot.parent = xRoot
else
yRoot.parent = xRoot
xRoot.rank = xRoot.rank + 1
These two techniques complement each other, and running time per operation is effectively a small constant. The algorithm can be implemented as follows in C++, Java, and Python: