Что такое тензор питон

What Are Tensors?

Tensors have been around ever since William Hamilton coined the term 200 years ago to describe a mathematical object representing a set of numbers with some transformation properties.

But Albert Einstein truly brought them into the spotlight by developing and formulating the whole theory of general relativity entirely in the language of tensors. Even though he wasn’t a big fan of tensors, Einstein popularized tensor calculus more than anyone else.

Definition of a Tensor

A tensor is a mathematical object that generalizes scalars, vectors, and matrices into higher-dimensional spaces. It’s an array of numbers and functions encompassing physical quantities, geometric transformations, and various mathematical entities. In a way, tensors are containers that present data in n-dimensions. They are typically grids of numbers called N-way arrays.

The word tensor, however, is still somewhat obscure. You won’t hear it in high school. Your math teacher may have never heard of it. But state-of-the-art machine learning frameworks are doubling down on tensors, with the most prominent example being Google’s TensorFlow.

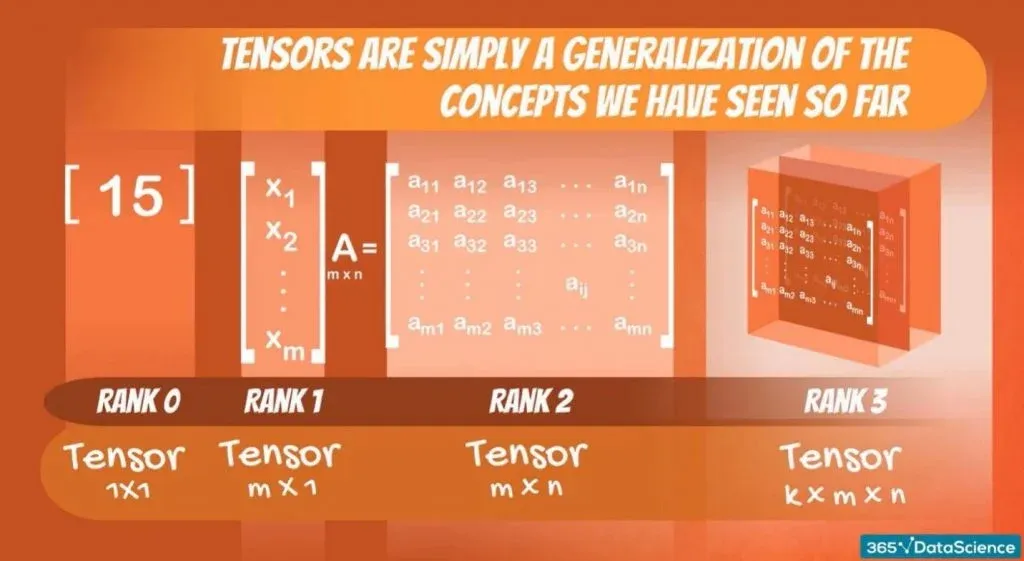
What Are Tensors?

The mathematical concept of a tensor could be broadly explained by describing a scalar as the lowest dimensionality and is always 1×1.

It can be considered a vector of length 1 or a 1×1 matrix. It’s followed by a vector, where each vector element is a scalar. The dimensions of a vector are nothing but Mx1 or 1xM matrices.

Then we have matrices, which are a collection of vectors. The dimensions of a matrix are MxN. In other words, a matrix is a collection of n vectors of dimensions m x 1. Alternatively, a matrix can be an array of m vectors of dimensions n x 1. Since scalars make up vectors, you can also think of a matrix as a collection of scalars.

Ranks

A rank is a fundamental concept that refers to a tensor’s number of indices or dimensions. It determines the types of operations a tensor can perform and thus plays a vital role in manipulating multi-dimensional data.

In this sense, scalars, vectors, and matrices are all tensors of ranks 0, 1, and 2, respectively. An object we haven’t seen is a tensor of rank 3. Its dimensions could be signified by k,m, and n, making it a KxMxN object. Such an object can be thought of as a collection of matrices.

How Do You Code a Tensor?

Let’s look at that in the context of Python. In terms of programming, a tensor is no different than a NumPy ndarray. You can store tensors in ndarrays—a common way to deal with the issue. Generally, it’s a two-step process.

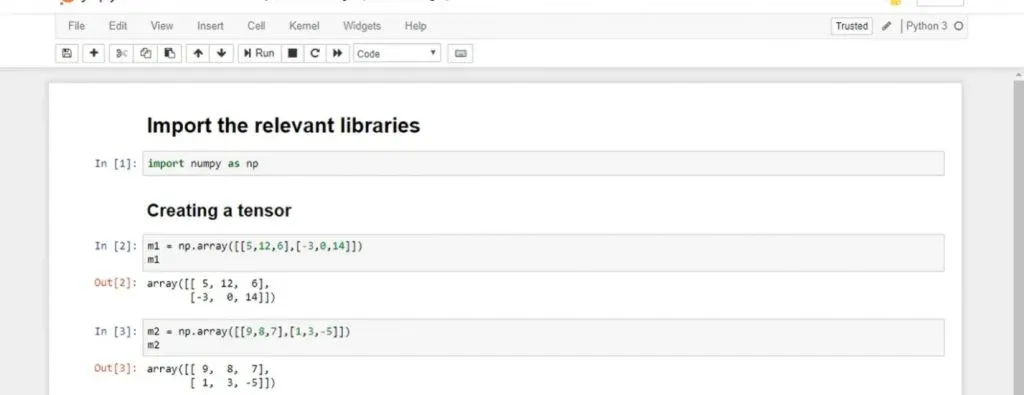
Step 1: Create a tensor out of the two following matrices.

• The first matrix, m1, will be a matrix with two vectors: [5, 12, 6] and [-3, 0, 14].
• The second matrix, m2, contains the following: [9, 8, 7] and [1, 3, -5].

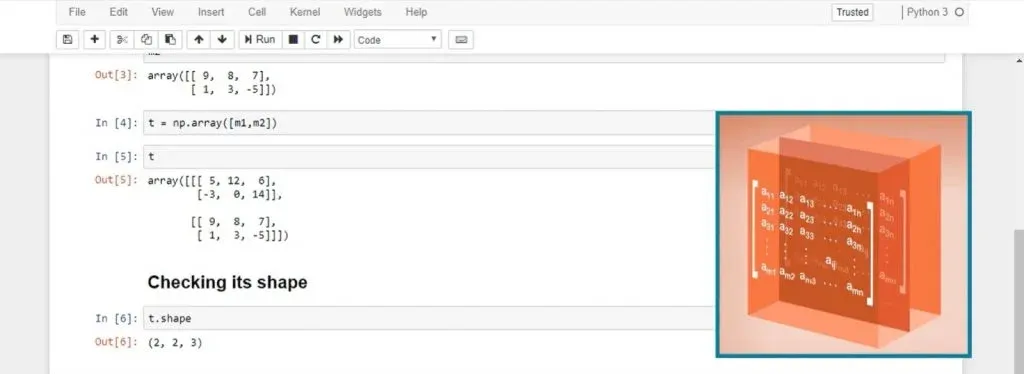
Step 2: Then, you can create an array, T, with two elements: m1 and m2. After printing T, you’ll realize that it contains both matrices:

It’s a 2x2x3 object containing two matrices, 2×3 each.

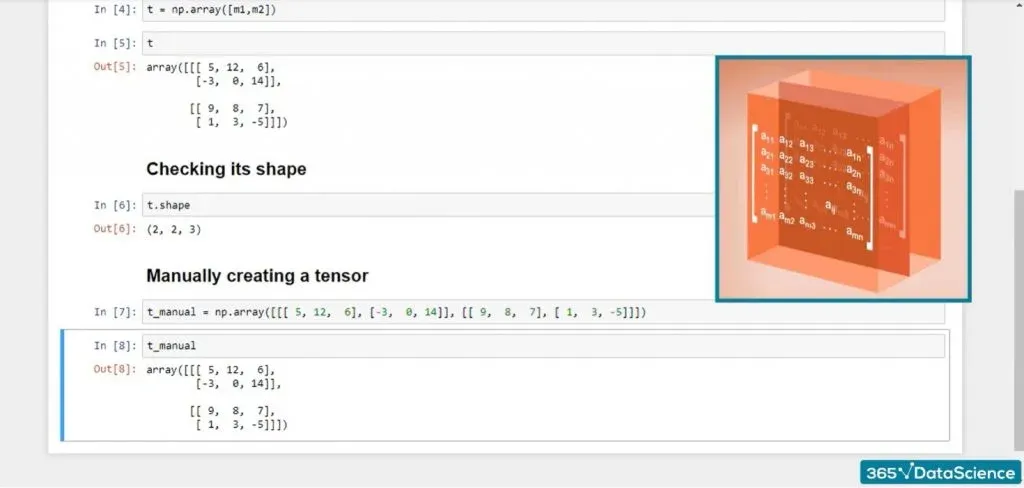
If you want to create the same tensor manually, you can write the following line of code:

With its many elements and confusing brackets, tensors are challenging to create by hand. You’ll mainly load, transform, and preprocess the data to obtain tensors. But it’s always good to have a theoretical background.

Why Are Tensors Useful in TensorFlow?

In machine learning, we often explain a single object with several dimensions. For instance, a photo is described by pixels—each with intensity, position, and (color) depth.

If we’re talking about a 3D movie experience, each eye could perceive a pixel differently. That’s where tensors come in handy and are incredibly scalable—no matter how many additional attributes we add to describe an object, we can always include an extra dimension to our tensor.

Today, we have various frameworks and programming languages. For instance, R is a famous vector-oriented programming language, meaning that the lowest unit is not an integer or a float but a vector.

In the same way, TensorFlow works with tensors, which not only optimizes CPU usage but also allows us to employ GPUs to make calculations. In 2016, Google developed Tensor Processing Units (TPUs)—processors that consider a tensor a building block for a calculation, not 0s and 1s, as does a CPU. This makes calculations exponentially faster.

If you wish to grow your machine and deep learning knowledge, tensors are a great addition to your toolkit. You can learn more in our Deep Learning with TensorFlow 2 and Convolutional Neural Networks with TensorFlow in Python courses.

Next Steps

Enroll in our Data Scientist Career Track and enhance your domain knowledge. Start with the fundamentals and dive right into our Statistics, Mathematics, and Probability courses. You can learn at your own pace in a step-by-step manner, sharpening your skills in SQL, Python, and TensorFlow. Sign up today and begin your data scientist career journey!

Источник

Работаем с тензорами в numpy

Сегодня рассмотрим, что такое тензоры, зачем они нужны в Machine Learning и как Python-библиотека NumPy помогает создавать их. Читайте в нашей статье про ранги тензоров и другие атрибуты этой структуры данных в Python.

Что такое тензоры и при чем тут Data Science

Числа — основа вычислений компьютера, и более того средство конечного отображения любых данных: от художественного текста до графики и видео. Методы Data Science и Machine Learning тоже трансформируют информацию в числовую форму, чтобы работать с ней. Такими наборами чисел являются тензоры – в Python-библиотеке NumPy структуры данных в виде массивов, т.е. array [1].Тензоры имеют следующие атрибуты:

• ранг – количество осей. В двумерном тензоре ранг равен 2, трехмерный — 3 и т.д.
• форма, определяющая количество элементов на каждой из осей;
• тип данных – int32, float32 и другие числовые типы.

Прежде чем начать работу с тензорами в библиотеке numpy, ее нужно импортировать. Для обращения к ней будем использовать символы np :

У массивов numpy есть атрибут ndim — ранг и shape — форма. Далее разберем на практических примерах, как с ними работать.

Скаляры и векторы в numpy

Тензор нулевого ранга или скаляр – это обычное число. В numpy он создается очень просто:

И форма у него отсутствует:

Тензор первого ранга или вектор – это массив скаляров, который создается следующим образом:

>>> a = np.array([1, 2, 3, 4, 5]) >>> a array([1, 2, 3, 4, 5])

Форма у вектора соответствует количеству элементов:

Тензоры 2-го ранга и выше в numpy

Тензор второго ранга или матрица представляет собой это массив векторов. В numpy он создается так:

>>> a = np.array([[1, 2, 13, 14], [5, 6, 17, 18], [9, 3, 11, 12]]) >>> a array([[ 1, 2, 13, 14], [ 5, 6, 17, 18], [ 9, 3, 11, 12]])

Форма у матрицы соответствует количеству строк и столбцов (3 строки и 4 столбца):

Тензор третьего ранга — это массив матриц без отдельного наименования. В numpy он создается следующим образом:

>>> a = np.array([[[10, 11, 12, 13], [14, 15, 16, 17], [18, 19, 20, 21]], [[22, 23, 24, 25], [26, 27, 28, 29], [30, 31, 32, 33]], [[34, 35, 36, 37], [38, 39, 40, 41], [42, 43, 44, 45]]]) >>> a array([[[10, 11, 12, 13], [14, 15, 16, 17], [18, 19, 20, 21]], [[22, 23, 24, 25], [26, 27, 28, 29], [30, 31, 32, 33]], [[34, 35, 36, 37], [38, 39, 40, 41], [42, 43, 44, 45]]])

Форма у тензора соответствует количеству матриц (3), числу строк (3) и столбцов (4) в каждой из них:

Тензор четвертого ранга — это массив тензоров третьего ранга, тензор пятого ранга — это массив тензоров четвертого ранга и т.д. Например, изображения можно закодировать как тензор 4-го ранга, а видео – как тензор 5-го ранга.

Где используются тензоры: применение в Data Science

Как мы уже отметили выше, тензоры позволяют представить изначально не числовую информацию в числовой форме. Например, изображение в оттенках серого представляется как матрица пикселей, где элемент равный 0 соответствует белому цвету, а 255 — черному, остальные являются переходными между белым и черным.

Совокупность таких изображений составляют образцы (samples). Тогда форма тензора с этими изображениями будет иметь вид: (образцы, высота, ширина)

У цветных изображений 3 канала цвета, поэтому его форма включает еще цвет: (образцы, цвет, высота, ширина).

Тексты можно представить виде матрицы, где предложение – это строка, а элемент в ней – закодированное слово. Видео – это совокупность изображений в каждом кадре, поэтому к форме тензора добавится атрибут в виде кадра.

В следующей статье мы продолжим разговор про тензоры в Data Science и Machine Learning и рассмотрим, как в Python можно управлять ими, извлекая из них нужные компоненты. Еще больше технических подробностей о работе с тензорами и представлением данных для Machine Learning, вы узнаете на практических курсах по Python в нашем лицензированном учебном центре обучения и повышения квалификации ИТ-специалистов в Москве.

Источник