Binary search trees in python

How to Implement Binary Search Tree in Python

In this tutorial, we will learn how to use a binary search tree in Python. Note that a binary tree is a non-linear data structure, while linked lists and arrays are linear data structures.

• Create a new tree with root key, nodes, and base elements also called leaf nodes.
• Determine the space and time complexity of this algorithm.
• Discuss various types of binary trees.

Table of contents

Prerequisites

To follow along with this tutorial, you must have:

1. An IDE (integrated development environment) that will aid in running our code. We will use Pycharm which can be downloaded here.
2. Some basic knowledge of Python.

Binary search tree

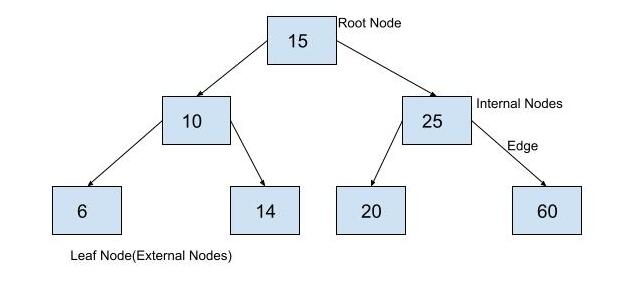
A binary tree is a set of finite nodes that can be empty or may contain several elements. A node is made up of three entities. A value with two pointers on the left and right. The root node is the parent component on each subtree.

It can also be considered as the topmost node in a tree. The nodes attached to the parent element are referred to as children. Leaf nodes, on the other hand, are the base elements in a binary tree.

Types of binary search trees

The various types of binary trees include:

1. Complete binary tree: All levels of the tree are filled and the root key has a sub-tree that contains two or no nodes.
2. Balanced binary tree: The leaf nodes are not far from the root which is more of a relative metric. The nodes can be more than a single level in a tree. A balanced tree is quite efficient when searching, inserting, and deleting components.
3. Full binary tree: It contains an equal number of nodes in each subtree except for the leaf nodes.

Creating a binary tree

We need the following Python syntax to generate a binary tree. A recursive function is required since the sub-tree has similar elements.

class binary_tree:  def __init__(self, key) #function to insert data to our binary tree  self.leftchild = None #setting leftchild of the tree to add items  self.rightchild = None #setting rightchild of the tree to add items  self.key = key  class binary_tree:  def __init__(self): #generate a tree to hold values  self.root = None  #this is the end 

Deleting a tree

To delete a tree we use the following code:

def add(self, value): #function to add data items to the tree  if self.key is None:  self.key = data #begin adding elements to the binary tree  return  if self.key == value: # this will take care for duplicate nodes  return  if value  self.key: #if value of the key node is more than the leftchild accept values  if self.leftchild:  self.leftchild.add(value) #set values to the leftchild of the tree  else:  self.leftchild = binary_tree(value)  else: #values are more than the key value  if self.rightchild: #if on the rigghtchild of the tree  self.rightchild.add(value) #set values to rightchild  else:  self.rightchild = binary_tree(value) #values cannot be less then the root key  ##End of search of our binary tree 

Adding data in tree

To add data to our tree, we use the following Python script:

root = binary_tree(50) # 50 is our root key and our object is root elements = 20,56,3,4,7,10,17,20> #adds values to the tree for i in elements:  root.add(i) #recursively adds values in the tree  root.search(10) 

Checking for empty nodes

The check() function below allows us to check for empty nodes:

def check(self,value): #check for empty values  if self.key is None: #if value is set to None  self.key = value 

Searching for a node in the tree

If we want to know whether a given node is there or not, we will compare the data of the given node with that in the root node.

First, we need to search whether the root key is equal to the given data. If the given node is present in the tree, we can print a message.

If the data is less than the root key, we will search on the left subtree, else, we look at the right subtree.

 def search(self, value):  if self.key == value: #check if value is equal to the key val  print("The node is present")  return  if value  self.key: #Here left subtree can be empty or it can contain one or more nodes  if self.leftchild: #this condition is true if left subtree exists  self.leftchild.search(value)  else:  print("The node is empty in the tree!")  else:  if self.rightchild:  self.rightchild.search(value) #search for all the values in the rightchild  return true  else:  print("The node is empty in the tree!") #print out empty rightchild nodes in the tree 

The table below summarizes the space and time complexity of the algorithm:

Binary Search Tree

Average	Worst case
Space	O(n)	O(n)
Access	O(log n)	O(n)
Search	O(log n)	O(n)
Insertion	O(log n)	O(n)
Removal	O(log n)	O(n)

Benefits of using binary search trees

• They allow fast lookup, addition, and deletion of items in a tree.
• It can be used to implement either dynamic sets of elements or lookup tables.
• They allow one to find an element using its key.
• They use a logarithmic time complexity of k = log(n) where k is the lookup, insertion, and removal time and n is the number of items stored in the tree. This is better than linear search time.

Conclusion

In this article we learned the definition and different types of binary search trees. We also discussed how to create a tree, as well as add and delete data. Finally, we looked at how to check for empty nodes.

Peer Review Contributions by: Wanja Mike

Источник

Binary Search Tree Implementation in Python

In this article, we will learn about binary search trees. We will study the underlying concepts behind binary search trees and then implement the code. You should be familiar with the concepts of binary trees to read this article.

What is a binary search tree?

A binary search tree is a binary tree data structure with additional properties along with the properties of binary trees. In a binary search tree,

• There are no duplicate values.
• The left subtree of a node has all the data values less than its own data. i.e. The left child or children of the left child are always less than the value in the current node.
• The right subtree of a node has all the data values greater than its own data. i.e. The right child or children of the right child of the current node are always greater than the current node.

This can be observed in the following Example.

Implementation of Binary Search Tree in Python

To implement a Binary Search Tree, we will use the same node structure as that of a binary tree which is as follows.

class BinaryTreeNode: def __init__(self, data): self.data = data self.leftChild = None self.rightChild=None

Now, to implement a binary search tree, we will implement functions to insert a value in the tree, search a value in the binary tree, and then we will see how to find the minimum and maximum elements from the binary search tree.

Insertion of a node in Binary Search Tree

While inserting a node in a binary search tree, three conditions may arise.

1. The Binary search tree can be empty. i.e. Root itself will be a value None.
2. The Value to be inserted is less than the root.
3. The value to be inserted is greater than the root.

To implement the first condition, we just make a new node and declare it as root. To implement second and third condition, We follow the following approach.

From the properties of a binary search tree, we can see that each sub tree is a binary search tree in itself. Thus we can consider each node as a root of another binary tree.

While inserting a new node, if the value of the new data is less than the value of the current node, we will add it to the left child of the binary search tree, otherwise, we will add it to the right child.

Proceeding recursively, we will always reach the first condition and then we will declare a new node and add the node to the binary search tree.

Following is the implementation of above approach.

class BinaryTreeNode: def __init__(self, data): self.data = data self.leftChild = None self.rightChild=None def insert(root,newValue): #if binary search tree is empty, make a new node and declare it as root if root is None: root=BinaryTreeNode(newValue) return root #binary search tree is not empty, so we will insert it into the tree #if newValue is less than value of data in root, add it to left subtree and proceed recursively if newValue
Root Node is: 15 left child of node is: 10 right child of node is: 25 Node is: 10 left child of node is: 6 right child of node is: 14 Node is: 25 left child of node is: 20 right child of node is: 60 Node is: 6 left child of node is: None right child of node is: None Node is: 14 left child of node is: None right child of node is: None Node is: 20 left child of node is: None right child of node is: None Node is: 60 left child of node is: None right child of node is: None
 
In the above output, we can verify every property of the binary search tree in our example. Here, after declaring the root node, no matter what the order of insertion of elements is there, the output will always be the same. Try this by copying and pasting this code in your own python IDE.
 
Searching an element in a binary search tree
 
We have seen above that a node with a value less than that of the current node’s value will always be in the left subtree of the current node and a node with a value greater than that of the current node’s value will always be in the right subtree of the current node. We will use this property to search an element in a binary search tree.
 
 
If the current node becomes empty, i.e. None, the element to be searched isn’t present in the tree and we will return False.
 
If the current node has a value equal to the search query, we will return True.
 
If the value to be searched is greater than the current node’s value, we will search the right subtree of the current node.
 
If the value to be searched is less than the current node’s value, we will search the left subtree of the current node
 
 
Implementation of the logic is given below.
 
class BinaryTreeNode: def __init__(self, data): self.data = data self.leftChild = None self.rightChild=None def insert(root,newValue): #if binary search tree is empty, make a new node and declare it as root if root is None: root=BinaryTreeNode(newValue) return root #binary search tree is not empty, so we will insert it into the tree #if newValue is less than value of data in root, add it to left subtree and proceed recursively if newValue

How to find the maximum element of a Binary Search Tree?
From whatever we have seen so far, we know that an element greater than the current node is always on its right side.
When we move to the right child of each node starting from root till end recursively, the greatest element will be present at the end.
So, to find the largest element of a binary search tree, we just have to find the rightmost element of the tree. Here is the implementation of this logic.
class BinaryTreeNode: def __init__(self, data): self.data = data self.leftChild = None self.rightChild=None def insert(root,newValue): #if binary search tree is empty, make a new node and declare it as root if root is None: root=BinaryTreeNode(newValue) return root #binary search tree is not empty, so we will insert it into the tree #if newValue is less than value of data in root, add it to left subtree and proceed recursively if newValue

How to find smallest element of a binary search tree?
We know that an element lesser than the current node is always on its left side. When we move to the left child of each node starting from root till end recursively, the smallest element will be present in the last.
So, to find the smallest element of a binary search tree, we just have to find the leftmost element of the tree. Here is the implementation of this logic.
class BinaryTreeNode: def __init__(self, data): self.data = data self.leftChild = None self.rightChild=None def insert(root,newValue): #if binary search tree is empty, make a new node and declare it as root if root is None: root=BinaryTreeNode(newValue) return root #binary search tree is not empty, so we will insert it into the tree #if newValue is less than value of data in root, add it to left subtree and proceed recursively if newValue

Conclusion
In this article, we have seen underlying concepts behind binary search trees. We have also implemented various operations like insertion, searching, finding the maximum element, and finding a minimum element in the binary search tree.
I would encourage you to implement the codes and play with them. Stay tuned for more informative tutorials.
Источник