- Rukovodstvo
- статьи и идеи для разработчиков программного обеспечения и веб-разработчиков.
- Двоичный поиск в Python
- Введение В этой статье мы углубимся в идею и реализацию двоичного поиска в Python. Двоичный поиск — это эффективный алгоритм поиска, работающий с отсортированными массивами. Он часто используется как один из первых примеров алгоритмов, которые работают в логарифмическом времени (O (logn)) из-за его интуитивного поведения, и является фундаментальным алгоритмом в компьютерных науках. Двоичный поиск — пример двоичного поиска работает по принципу «разделяй и властвуй» и полагается на то, что массив отсортирован.
- Вступление
- Двоичный поиск — пример
- Реализация двоичного поиска
- Рекурсивный
- Итеративный
- Заключение
- Python. Бинарный поиск в массиве
- Заключение
- Двоичный, или бинарный, поиск элемента
- Описание алгоритма
- Исходный код на Python
Rukovodstvo
статьи и идеи для разработчиков программного обеспечения и веб-разработчиков.
Двоичный поиск в Python
Введение В этой статье мы углубимся в идею и реализацию двоичного поиска в Python. Двоичный поиск — это эффективный алгоритм поиска, работающий с отсортированными массивами. Он часто используется как один из первых примеров алгоритмов, которые работают в логарифмическом времени (O (logn)) из-за его интуитивного поведения, и является фундаментальным алгоритмом в компьютерных науках. Двоичный поиск — пример двоичного поиска работает по принципу «разделяй и властвуй» и полагается на то, что массив отсортирован.
Вступление
В этой статье мы погрузимся в идею и реализацию двоичного поиска в Python.
Двоичный поиск — это эффективный алгоритм поиска, работающий с отсортированными массивами. Он часто используется как один из первых примеров алгоритмов, которые работают в логарифмическом времени ( O (logn) ) из-за его интуитивного поведения, и является фундаментальным алгоритмом в компьютерных науках.
Двоичный поиск — пример
Двоичный поиск работает по принципу «разделяй и властвуй» и полагается на тот факт, что массив сортируется для исключения половины возможных кандидатов на каждой итерации. В частности, он сравнивает средний элемент отсортированного массива с элементом, который он ищет, чтобы решить, где продолжить поиск.
Если целевой элемент больше среднего элемента — он не может быть расположен в первой половине коллекции, поэтому он отбрасывается. То же самое и наоборот.
Примечание. Если в массиве четное количество элементов, не имеет значения, с какого из двух «средних» элементов мы начнем.
Давайте быстро рассмотрим пример, прежде чем мы продолжим объяснять, как работает двоичный поиск:
Как мы видим, мы точно знаем, что, поскольку массив отсортирован, x не находится в первой половине исходного массива.
Когда мы знаем, в какой половине исходного массива x находится, мы можем повторить этот точный процесс с этой половиной и снова разделить его на половины, отбросив половину, которая наверняка не содержит x :
Мы повторяем этот процесс, пока не получим подмассив, содержащий только один элемент. Мы проверяем, является ли этот элемент x . Если это так
Если вы внимательно посмотрите на это, вы можете заметить, что в худшем случае ( x не существует в массиве) нам нужно проверить гораздо меньшее количество элементов, чем нам нужно в несортированном массиве, что потребует чего-то большего, вроде линейного поиска , что безумно неэффективно.
Чтобы быть более точным, количество элементов, которые нам нужно проверить в худшем случае, равно log ~2~ N, где N — количество элементов в массиве.
Это оказывает большее влияние, чем больше массив:
Если бы в нашем массиве было 10 элементов, нам нужно было бы проверить только 3 элемента, чтобы либо найти x, либо сделать вывод, что его там нет. Это 33,3%.
Однако, если бы в нашем массиве было 10 000 000 элементов, нам нужно было бы проверить только 24 элемента. Это 0,0002%.
Реализация двоичного поиска
Двоичный поиск — это естественно рекурсивный алгоритм, поскольку один и тот же процесс повторяется для все меньших и меньших массивов, пока не будет найден массив размером 1. Однако, конечно же, существует итеративная реализация, и мы продемонстрируем оба подхода.
Рекурсивный
Начнем с рекурсивной реализации, поскольку она более естественна:
def binary_search_recursive(array, element, start, end): if start > end: return -1 mid = (start + end) // 2 if element == array[mid]: return mid if element < array[mid]: return binary_search_recursive(array, element, start, mid-1) else: return binary_search_recursive(array, element, mid+1, end) Давайте подробнее рассмотрим этот код. Выходим из рекурсии, если start элемент выше end :
Это связано с тем, что такая ситуация возникает только тогда, когда элемент не существует в массиве. Что происходит, так это то, что у нас остается только один элемент в текущем подмассиве, и этот элемент не соответствует тому, который мы ищем.
На этом этапе start равно end . Однако, поскольку element не равен array[mid] , мы снова «разбиваем» массив таким образом, что либо уменьшаем end на 1, либо увеличиваем start на единицу, и при этом условии существует рекурсия.
Мы могли бы сделать это, используя другой подход:
if len(array) == 1: if element == array[mid]: return mid else: return -1 Остальная часть кода выполняет логику «проверить средний элемент, продолжить поиск в соответствующей половине массива». Мы находим индекс среднего элемента и проверяем, соответствует ли ему искомый элемент:
mid = (start + end) // 2 if elem == array[mid]: return mid Если нет, мы проверяем, больше ли элемент или меньше среднего:
Давайте продолжим и запустим этот алгоритм с небольшой модификацией, чтобы он распечатал, над каким подмассивом он работает в настоящее время:
element = 18 array = [1, 2, 5, 7, 13, 15, 16, 18, 24, 28, 29] print("Searching for <>".format(element)) print("Index of <>: <>".format(element, binary_search_recursive(array, element, 0, len(array)))) Выполнение этого кода приведет к:
Searching for 18 Subarray in step 0:[1, 2, 5, 7, 13, 15, 16, 18, 24, 28, 29] Subarray in step 1:[16, 18, 24, 28, 29] Subarray in step 2:[16, 18] Subarray in step 3:[18] Index of 18: 7 Ясно видно, как он вдвое сокращает пространство поиска на каждой итерации, приближаясь к элементу, который мы ищем. Если бы мы попытались найти элемент, которого нет в массиве, результат был бы таким:
Searching for 20 Subarray in step 0: [4, 14, 16, 17, 19, 21, 24, 28, 30, 35, 36, 38, 39, 40, 41, 43] Subarray in step 1: [4, 14, 16, 17, 19, 21, 24, 28] Subarray in step 2: [19, 21, 24, 28] Subarray in step 3: [19] Index of 20: -1 И просто для удовольствия, мы можем попробовать выполнить поиск в некоторых больших массивах и посмотреть, сколько шагов требуется двоичный поиск, чтобы выяснить, существует ли число:
Searching for 421, in an array with 200 elements Search finished in 6 steps. Index of 421: 169 Searching for 1800, in an array with 1500 elements Search finished in 11 steps. Index of 1800: -1 Searching for 3101, in an array with 3000 elements Search finished in 8 steps. Index of 3101: 1551 Итеративный
Итерационный подход очень прост и похож на рекурсивный подход. Здесь мы просто выполнить проверку в виде в while цикла:
def binary_search_iterative(array, element): mid = 0 start = 0 end = len(array) step = 0 while (start : <>".format(step, str(array[start:end+1]))) step = step+1 mid = (start + end) // 2 if element == array[mid]: return mid if element < array[mid]: end = mid - 1 else: start = mid + 1 return -1 Давайте заполним массив и найдем в нем элемент:
array = [1, 2, 5, 7, 13, 15, 16, 18, 24, 28, 29] print("Searching for <> in <>".format(element, array)) print("Index of <>: <>".format(element, binary_search_iterative(array, element))) Выполнение этого кода дает нам результат:
Searching for 18 in [1, 2, 5, 7, 13, 15, 16, 18, 24, 28, 29] Subarray in step 0: [1, 2, 5, 7, 13, 15, 16, 18, 24, 28, 29] Subarray in step 1: [16, 18, 24, 28, 29] Subarray in step 2: [16, 18] Subarray in step 3: [18] Index of 18: 7 Заключение
Двоичный поиск - это невероятный алгоритм для использования с большими отсортированными массивами или всякий раз, когда мы планируем многократно искать элементы в одном массиве.
Стоимость однократной сортировки массива и последующего использования двоичного поиска для поиска элементов в нем несколько раз намного лучше, чем использование линейного поиска в несортированном массиве, чтобы мы могли избежать затрат на его сортировку.
Если мы сортируем массив и ищем элемент только один раз, более эффективно просто выполнить линейный поиск в несортированном массиве.
Если вы хотите прочитать об алгоритмах сортировки в Python , мы вам поможем!
Licensed under CC BY-NC-SA 4.0
Python. Бинарный поиск в массиве
В этой статье мы рассмотрим Двоичный (бинарный) поиск - один из классических алгоритмов поиска элемента в отсортированном массиве.
Предположим вы знаете в каком месяце родился ваш друг(пусть это будет сентябрь) , но не знаете в какой день. И вам нужно за наименьшее количество попыток определить в какой день месяца он родился. И при этом вам ваш друг на каждую вашу попытку будет давать один их трех ответов: "мало", "много" или "угадал"
Самый простой способ это метод простого поиска. Вы перебираете все варианты подряд 1, 2, 3 и далее.Конечно , если ваш друг родился 3 сентября вам понадятся всего лишь три попытки , но если 24 сентября , то вам нужно 24 попытки. А если друг родился 30 сентября , то нужны все 30 попыток.
Рассмотрим другой более эффективный метод поиска.
Допустим , что у нашего друга день рождения 24 сентября. Так как исходный массив содержит 30 элементов , то мы на первом шаге назовем элемент который находится посередине этого массива. Это число 15. Наш друг говорит , что "мало". И теперь мы понимаем , что все числа меньше 15 и само число 15 можно исключить из поиска и можно сосредоточиться на числах, которые больше 15.
На втором шаге мы назовем число которое находится посередине чисел от 16 до 30 и этим числом является 23 , но это тоже меньше искомого числа. И поэтому мы исключаем все числа меньше 23 и само число 23.
И так мы повторяем пока не найдем искомое число.В нашем случае это число 24.
Ниже на рисунке для наглядности показаны все шаги нахождения искомого числа(число 24) методом бинарного поиска
Чтобы найти число 24 в массиве из 30 элементов при помощи простого поиска нам нужно 24 попытки , то при помощи бинарного поиска нам потребовалось всего лишь 5 попыток. То есть в массиве из 30 элементов мы гарантированно за 5 попыток можем найти любой элемент, так log 30 примерно будет равно 5.
А что будет если у нас количество элементов равно не 30 , а скажем 1000? То тогда при простом поиске(переборе) , чтобы найти число 1000 нужно сделать 1000 итераций(попыток). А вот при бинарном поиске нужно сделать всего лишь 10 попыток , потому что 2 в 10 степени это 1024. Для 10 тысячи элементов при бинарном поиске нужно всего лишь 14 попыток , а вот при переборе количество попыток растет линейно. В этом и мощь бинарного алгоритма и его широкое распространение.
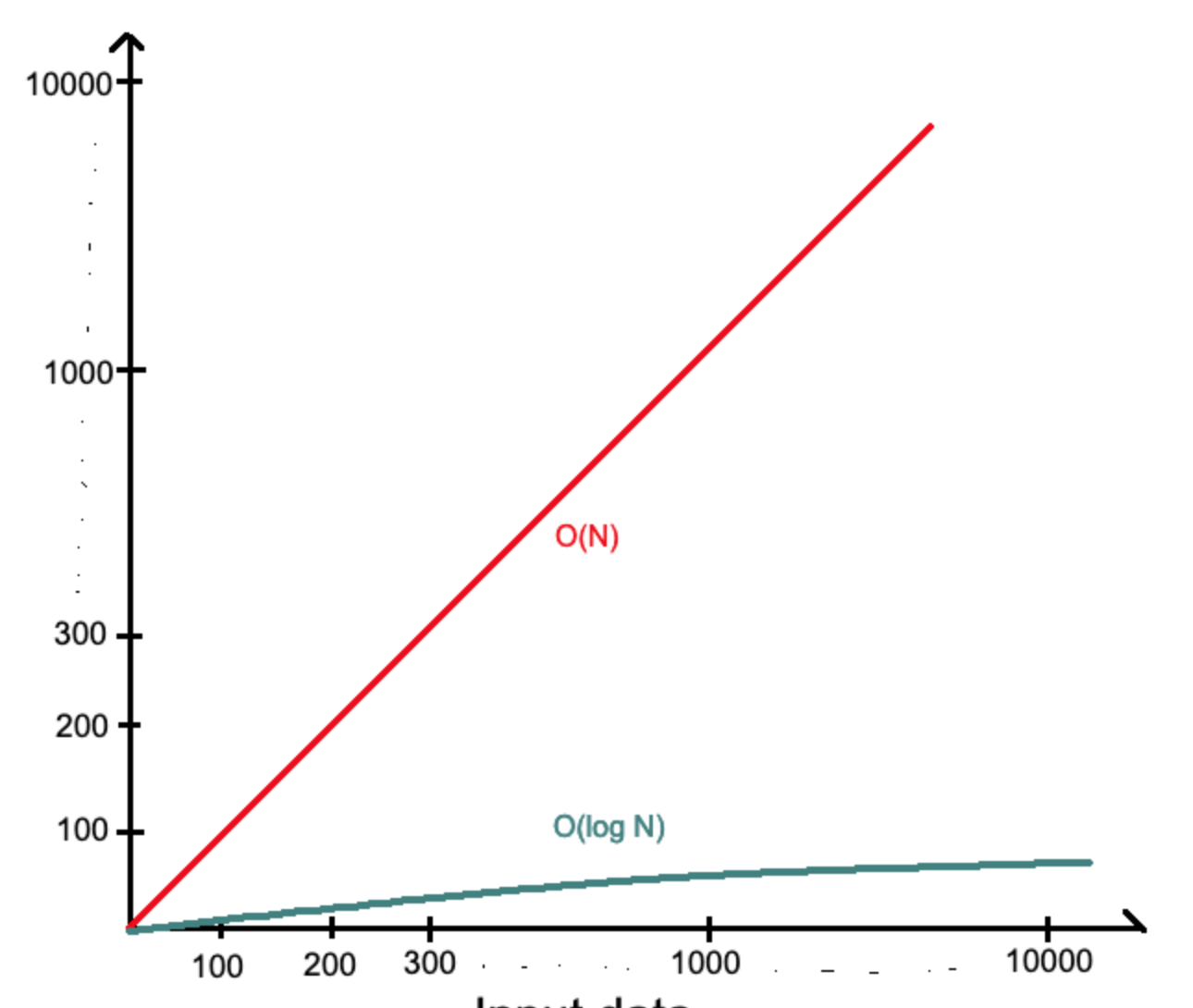
O(log n) — логарифмическая сложность для бинарного поиска
O(n) — Линейная сложность для простого поиска
Сравнение линейной и логарифмической функций.
Реализация алгоритма бинарного поиска на Python.
def binary_search(sequence, start_element, key): end_element = len(sequence) - 1 while start_element Заключение
В данной статье мы рассмотрели один из классических алгоритмов поиска. Это бинарный поиск элемента в отсортированном массиве.
Двоичный, или бинарный, поиск элемента
Двоичный, или бинарный, поиск значения в списке или массиве используется только для упорядоченных последовательностей, то есть отсортированных по возрастанию или убыванию. Заключается в определении, содержит ли массив искомое значение, а также в определение места его нахождения.
При решении задачи на языке программирования Python вместо массива используется список
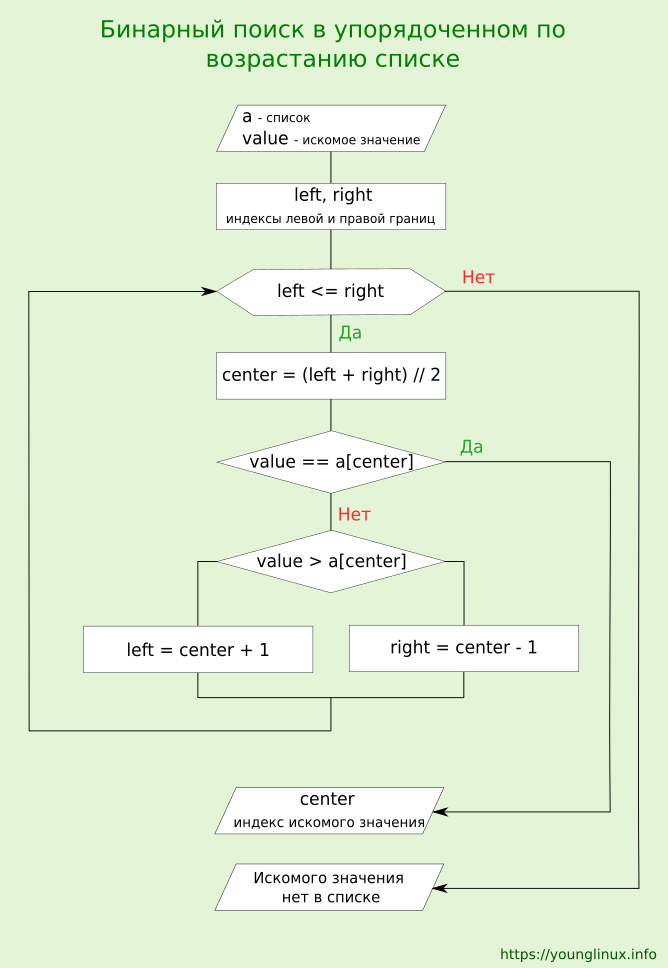
Описание алгоритма
- Находится средний элемент последовательности. Для этого первый и последний индексы связываются с переменными, а индекс среднего элемента вычисляется.
- Значение среднего элемента сравнивается с искомым значением. Если значение среднего элемента оказывается равным искомому, поиск завершается.
- Иначе, в зависимости от того, искомое значение больше или меньше значения среднего элемента, дальнейший поиск будет происходить только в левой или только в правой половинах массива.
- Для этого одна из границ исследуемой последовательности сдвигается. Если искомое значение больше значения среднего элемента, то нижняя граница сдвигается за средний элемент на один элемент справа. Если искомое значение меньше значения среднего элемента, то верхняя граница сдвигается на элемент перед средним.
- Снова находится средний элемент теперь уже в выбранной половине. Описанный выше алгоритм повторяется для данного среза.
Исходный код на Python
from random import randint # Создание списка, # его сортировка по возрастанию # и вывод на экран a = [] for i in range(10): a.append(randint(1, 50)) a.sort() print(a) # искомое число value = int(input()) mid = len(a) // 2 low = 0 high = len(a) - 1 while a[mid] != value and low high: if value > a[mid]: low = mid + 1 else: high = mid - 1 mid = (low + high) // 2 if low > high: print("No value") else: print("ID =", mid)
[6, 17, 21, 27, 32, 35, 35, 36, 37, 48] 27 ID = 3
[4, 5, 12, 13, 13, 18, 22, 26, 30, 35] 28 No value
Другие варианты решения задачи двоичного поиска на Python:
from random import randint a = [randint(1, 50) for i in range(10)] a.sort() print(a) value = int(input()) left = 0 right = len(a) - 1 center = (left + right) // 2 while a[center] != value: if value > a[center]: left = center + 1 else: right = center - 1 center = (left + right) // 2 if left >= right: break if value == a[center]: print("ID =", center) else: print("No value")
from random import randint a = [randint(1, 50) for i in range(10)] a.sort() print(a) value = int(input()) left = 0 right = len(a) - 1 while left right: center = (left + right) // 2 if value == a[center]: print("ID =", center) break if value > a[center]: left = center + 1 else: right = center - 1 else: print("No value")