Алгоритм сжатия хаффмана python

Saved searches

Use saved searches to filter your results more quickly

You signed in with another tab or window. Reload to refresh your session. You signed out in another tab or window. Reload to refresh your session. You switched accounts on another tab or window. Reload to refresh your session.

Python Implementaion of Huffman Coding — compression and decompression

bhrigu123/huffman-coding

This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.

Name already in use

A tag already exists with the provided branch name. Many Git commands accept both tag and branch names, so creating this branch may cause unexpected behavior. Are you sure you want to create this branch?

Sign In Required

Please sign in to use Codespaces.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching Xcode

If nothing happens, download Xcode and try again.

Launching Visual Studio Code

Your codespace will open once ready.

There was a problem preparing your codespace, please try again.

Latest commit

Git stats

Files

Failed to load latest commit information.

README.md

Python Implementaion of Huffman Coding

Consists compress and decompress function.

Testing / Running the program

1. Save / Clone the above repository
2. The repository consists of a sample text file of size 715kB
3. Run the python code useHuffman.py to compress & decompress the given sample file. For eg. open terminal and run python3 useHuffman.py
4. The above command will perform compression and decompression on the sample.txt file present here. Both the compressed and decompressed file will be present at the same location.

To run the code for compression of any other text file, edit the path variable in the useHuffman.py file.

For now, the decompress() function is to be called from the same object from which the compress() function was called. (as the encoding information is stored in the data members of the object only)

About

Python Implementaion of Huffman Coding — compression and decompression

Источник

Алгоритм сжатия кода Хаффмана

Кодирование Хаффмана (также известное как кодирование Хаффмана) — это алгоритм сжатия данных, который формирует основную идею сжатия файлов. В этом посте рассказывается о кодировании с фиксированной и переменной длиной, уникально декодируемых кодах, правилах префиксов и построении дерева Хаффмана.

Обзор

Мы уже знаем, что каждый символ представляет собой последовательность 0’s а также 1’s и хранится с использованием 8-бит. Это известно как “кодирование с фиксированной длиной”, так как каждый символ использует одинаковое количество фиксированных битов памяти.

Учитывая текст, как уменьшить количество места, необходимое для хранения символа?

Идея состоит в том, чтобы использовать “кодирование переменной длины”. Мы можем использовать тот факт, что одни символы встречаются в тексте чаще, чем другие (см. это) для разработки алгоритма, который может представлять тот же фрагмент текста, используя меньшее количество битов. При кодировании с переменной длиной мы присваиваем символам переменное количество битов в зависимости от их частоты в данном тексте. Таким образом, некоторые символы могут в конечном итоге занимать один бит, а некоторые — два бита, некоторые могут быть закодированы с использованием трех битов и так далее. Проблема с кодированием переменной длины заключается в его декодировании.

Учитывая последовательность битов, как ее однозначно декодировать?

Рассмотрим строку aabacdab . Оно имеет 8 символов в нем и использует 64-битное хранилище (с использованием кодирования фиксированной длины). Если принять во внимание, что частота символов a , b , c а также d находятся 4 , 2 , 1 , 1 , соответственно. Попробуем представить aabacdab используя меньшее количество битов, используя тот факт, что a встречается чаще, чем b , а также b встречается чаще, чем c а также d . Начнем со случайного присвоения однобитового кода 0 к a , 2-битный код 11 к b , и 3-битный код 100 а также 011 к персонажам c а также d , соответственно.

Итак, строка aabacdab будет закодирован в 00110100011011 (0|0|11|0|100|011|0|11) используя приведенные выше коды. Но настоящая проблема заключается в расшифровке. Если мы попытаемся декодировать строку 00110100011011 , это приведет к неоднозначности, так как его можно декодировать,

0|011|0|100|011|0|11 adacdab
0|0|11|0|100|0|11|011 aabacabd
0|011|0|100|0|11|0|11 adacabab
…
and so on

Чтобы предотвратить двусмысленность при декодировании, мы обеспечим соответствие нашего кодирования “правилу префикса”, что приведет к “уникально декодируемым кодам”. Правило префикса гласит, что ни один код не является префиксом другого кода. Под кодом мы подразумеваем биты, используемые для определенного символа. В приведенном выше примере 0 является префиксом 011 , что нарушает правило префикса. Если наши коды удовлетворяют префиксному правилу, декодирование будет однозначным (и наоборот).

Давайте снова рассмотрим приведенный выше пример. На этот раз мы присваиваем символам коды, удовлетворяющие правилу префикса. ‘a’ , ‘b’ , ‘c’ , а также ‘d’ .

Используя приведенные выше коды, строка aabacdab будет закодирован в 00100110111010 (0|0|10|0|110|111|0|10) . Теперь мы можем однозначно декодировать 00100110111010 вернуться к нашей исходной строке aabacdab .

Теперь, когда мы разобрались с кодированием переменной длины и правилом префиксов, давайте поговорим о кодировании Хаффмана.

Кодирование Хаффмана

Техника работает, создавая бинарное дерево узлов. Узел может быть листовым узлом или внутренним узлом. Изначально все узлы являются листовыми узлами, которые содержат сам персонаж, вес (частоту появления) персонажа. Внутренние узлы содержат вес символов и ссылки на два дочерних узла. По общему соглашению, бит 0 представляет следующий левый дочерний элемент, и немного 1 представляет следующий правильный ребенок. Готовое дерево имеет n листовые узлы и n-1 внутренние узлы. Рекомендуется, чтобы дерево Хаффмана отбрасывало неиспользуемые символы в тексте, чтобы получить наиболее оптимальную длину кода.

Мы будем использовать приоритетная очередь для построения дерева Хаффмана, где узел с наименьшей частотой имеет наивысший приоритет. Ниже приведены полные шаги:

1. Создайте конечный узел для каждого символа и добавьте их в очередь приоритетов.

2. Пока в queue больше одного узла:

• Удалите из queue два узла с наивысшим приоритетом (самой низкой частотой).
• Создайте новый внутренний узел с этими двумя узлами в качестве дочерних элементов и частотой, равной сумме частот обоих узлов.
• Добавьте новый узел в очередь приоритетов.

3. Оставшийся узел является корневым узлом, и дерево завершено.

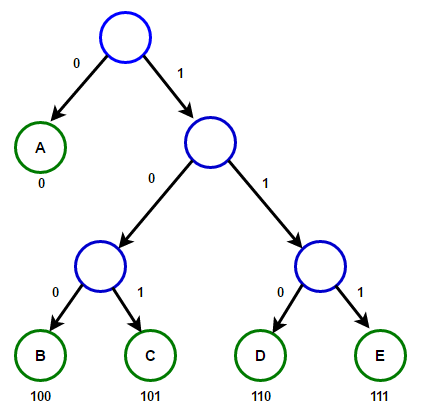
Рассмотрим некоторый текст, состоящий только из ‘A’ , ‘B’ , ‘C’ , ‘D’ , а также ‘E’ символов, а их частота 15 , 7 , 6 , 6 , 5 , соответственно. Следующие рисунки иллюстрируют шаги, за которыми следует алгоритм:

Путь от корня к любому конечному узлу хранит оптимальный код префикса (также называемый кодом Хаффмана), соответствующий символу, связанному с этим конечным узлом.

Реализация

Ниже приведена реализация алгоритма сжатия кода Хаффмана на C++, Java и Python:

Источник

Метод Хаффмана в Python

Метод Хаффмана – это алгоритм оптимального префиксного кодирования, используемый для сжатия данных. В этой статье мы рассмотрим, как реализовать алгоритм Хаффмана в Python.

Основы алгоритма Хаффмана

Основная идея алгоритма Хаффмана заключается в том, чтобы присвоить короткие коды символам с высокой частотой встречаемости и более длинные коды символам с меньшей частотой. Это позволяет сжимать данные без потерь, так как коды символов уникальны и не пересекаются.

Реализация алгоритма Хаффмана в Python

Для реализации алгоритма Хаффмана в Python нам потребуется создать две основные функции: одну для построения дерева Хаффмана и другую для генерации кодов Хаффмана на основе этого дерева.

Построение дерева Хаффмана

 import heapq from collections import defaultdict def build_huffman_tree(symbols_freq): heap = [[weight, [symbol, ""]] for symbol, weight in symbols_freq.items()] heapq.heapify(heap) while len(heap) > 1: lo = heapq.heappop(heap) hi = heapq.heappop(heap) for pair in lo[1:]: pair[1] = '0' + pair[1] for pair in hi[1:]: pair[1] = '1' + pair[1] heapq.heappush(heap, [lo[0] + hi[0]] + lo[1:] + hi[1:]) return heap[0] 

Генерация кодов Хаффмана

 def generate_huffman_codes(tree): huff_codes = <> for pair in tree[1:]: symbol, code = pair huff_codes[symbol] = code return huff_codes 

Использование алгоритма Хаффмана

Теперь мы можем использовать алгоритм Хаффмана для сжатия и распаковки данных. В следующем примере

В следующем примере мы сжимаем и затем восстанавливаем исходное сообщение:

Сжатие данных с использованием кодов Хаффмана

 def compress_data(text, huff_codes): compressed_data = "" for char in text: compressed_data += huff_codes[char] return compressed_data 

Восстановление данных

 def decompress_data(compressed_data, huff_codes): huff_codes_reversed = decoded_data = "" temp_code = "" for bit in compressed_data: temp_code += bit if temp_code in huff_codes_reversed: decoded_data += huff_codes_reversed[temp_code] temp_code = "" return decoded_data 

Пример использования алгоритма Хаффмана

Давайте проверим работу нашего алгоритма на примере:

 text = "абракадабра" # Подсчет частоты символов в тексте symbols_freq = defaultdict(int) for symbol in text: symbols_freq[symbol] += 1 # Построение дерева Хаффмана и генерация кодов huffman_tree = build_huffman_tree(symbols_freq) huffman_codes = generate_huffman_codes(huffman_tree) # Сжатие и распаковка данных compressed_data = compress_data(text, huffman_codes) decompressed_data = decompress_data(compressed_data, huffman_codes) print(f"Исходный текст: ") print(f"Сжатые данные: ") print(f"Восстановленный текст: ") 

Результат работы алгоритма должен выглядеть следующим образом:

 Исходный текст: абракадабра Сжатые данные: 1101000110101101000 Восстановленный текст: абракадабра 

В этом примере мы сжали и успешно восстановили исходный текст, используя алгоритм Хаффмана, реализованный на языке Python.

Источник